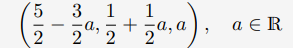Linear Algebra

선형대수학은 벡터와 벡터들을 다루는 법칙에 관한 학문이다.

여기서 벡터란 흔히 우리가 떠올리는 기하학적 벡터 이외에도 여러가지를 뜻한다.

1. 기하학적 벡터는 우리에게 가장 친숙한 벡터로 두개의 기하학적 벡터를 더하면 또다른 기하학적
   벡터가 되고특정 벡터에 스칼라값을 곱해도 계속 기하학적 벡터의 형태를 띈다.

2. 다항식 또한 백터라고 할 수 있는데 두개의 서로 다른 다항식을 더하면 또다른 다항식이 되고 다항식에 스칼락밧을 곱해도 여전히 다항식의 형태를 띄므로 벡터의 성질을 가지기 때문이다.

3. 소리신호들을 합쳐도 소리신호이고 소리 신호를 조정해도 여전히 소리신호이므로 소리신호도 벡터라고 할 수 있다.

4. n개의 숫자로 이루어진 튜플 Rⁿ또한 벡터의 성질을 띄므로 벡터이다.
   

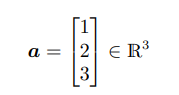
선형방정식

선형방정식은 선형대수학에서 가장 중요한 부분이다. 많은 문제들이 선형방정식의 구조로 형식화 되고 선형대수학이 그러한 문제들을 푸는 도구가 된다.

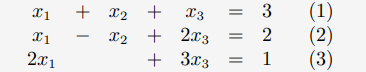
위의 선형방정식에서 해는 없다. (1)식과 (2)식을 더하면 (3)식과 모순되는 방정식이 나오기 때문이다.

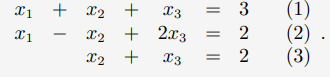
위의 식에서는 (1, 1, 1)이라는 유일한 해가 나온다.

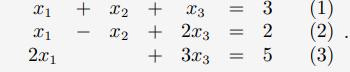
위의 식에서는 x3를 a라는 변수로 두고 무수히 많은 해를 얻을 수 있다.

위와 같이 선형방정식을 풀 수 없을 때에는 선형회귀를 이용하여 선형방정식을 풀 수 있다.