Ch2-2.Matrices

Matrices

행렬은 선형대수학에서 매운 중요하며, 연립선형방정식을 간결히 표현하는데에 사용된다.
다음과 같은 행렬 A는 m,n 튜플로 표현되는 실수 $a_{ij}$를 요소로 가지며 m개의 행과 n개의 열로 구성된다. 행과 열은 행벡터, 열벡터라고도 부른다.

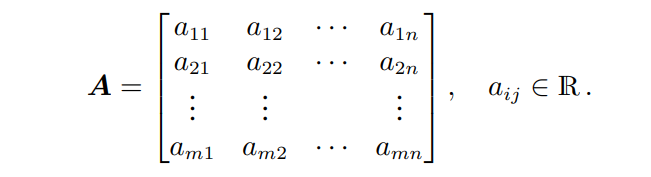
행렬A는 모든 열을 일렬로 쌓아 하나의 긴 벡터로 표현가능하다.

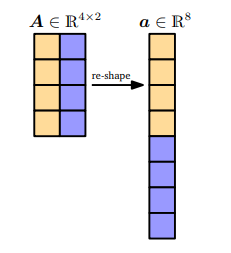
Matrix Addition and Mulitplication

두 행렬의 합은 element-wise 로 정의되며 다음과 같다.

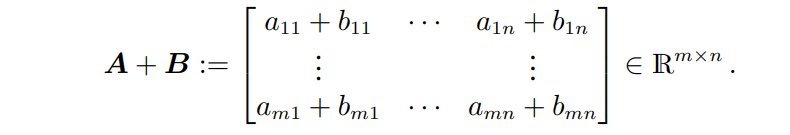
두 행렬의 곱 C = AB의 요소 $c_{ij}$는 다음과 같이 계산된다.

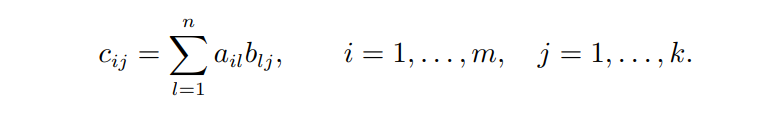
단위행렬은 대각성분이 모두 1이고 나머지 요소들은 모두 0인 n x n 행렬이다.

행렬의 성질

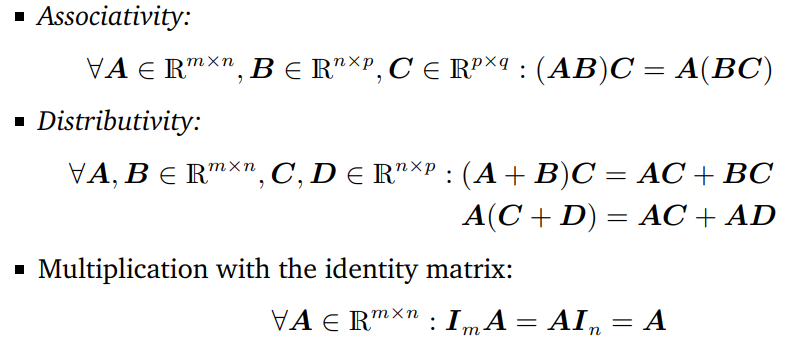
Inverse and Transpose

A행렬이 n x n 정사각 행렬일 때, 다음과 같은 성질을 만족하는 n x n 행렬 B는 A의 역행렬이라고 하고 $A^{-1}$로 표기된다.

다만, 모든 행렬에서 역행렬이 존재하는 것은 아니다. 역행렬이 존재하는 행렬을 regular/invertible/nonsingular라고 부르며, 역행렬이 존재하지 않는 행렬은 singular/noninvertible이라고 부른다. 역행렬이 존재할 때 역행렬은 유일하다.

행렬 A, B가 다음과 같을 때, AB는 다음과 같다.



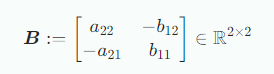
$a_{11}a_{22} - a_{12}a_{21}$ != 0일 때 역행렬이 존재하고 다음과 같다.

$a_{11}a_{22} - a_{12}a_{21}$는 2 x 2행렬의 행렬식이다.

행령 B가 A의 전치일 때, B = $A^T$로 표기하며 A의 열을 행으로 바꿔 얻을 수 있다. 다음은 전치행렬과 역행렬의 중요 속성이다.

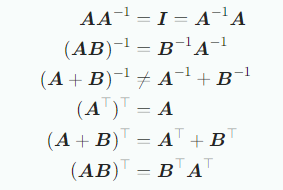
A = $A^T$ 을 만족할 때, 행렬 A 를 대칭적이라고 하고, symmetric matrix(대칭 행렬)라고 부릅니다.

대칭행렬은 정사각행렬이며 A의 역행렬이 존재하면 $A^T$도 존재하며 두 행렬이 대칭행렬이어도 두 행렬들의 곱도 항상 대칭인 것은 아니다.

Multiplication by a Scalar

스칼라 값 λ와 행렬 A를 곱하면 다음과 같으며 두 스칼라 값 λ,ψ 에 대해서 다음의 속성들을 만족합니다

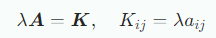
Compact Representations of Systems of Linear Equations

다음과 같은 연립선형방정식이 있을 때,

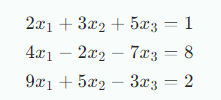
행렬의 곱셈법칙을 사용하여 다음처럼 간략한 형태로 작성할 수 있다.

일반적으로 모든 연립선형방정식은 $Ax=b$ 의 형태로 표현할 수 있습니다.