벨만-포드 알고리즘(Bellman-Ford Algorithm)이란?

-
벨만-포드 알고리즘은 한 노드에서 다른 노드까지의 최단 거리를 구하는 알고리즘이다. -
간선의 가중치가 음수일 때도 최단 거리를 구할 수 있다.
우리가 알고있는 다익스트라 알고리즘도 최단 거리를 구하는 알고리즘인데, '벨만-포드는 또 뭘까?'라는 생각이 들 수 있다. 다익스트라와 벨만-포드의 차이점에 대해 알아보자.
벨만-포드 vs 다익스트라
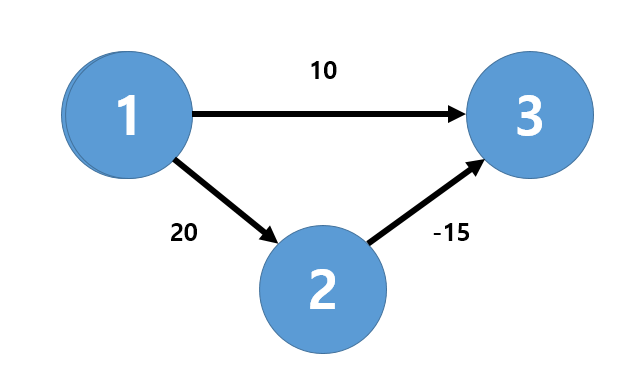
위 그림을 보자. 우리는 '1번 노드에서 3번 노드로 가는 최단 거리'를 구한다고 가정하자. 우리의 육안으로 보면 '1번 -> 3번'으로 가는 경로는 2가지이다. 1번 -> 3번(cost:10)과 1번 -> 2번 -> 3번(cost:20-15=5) 2가지로, '1번 노드에서 3번 노드로 가는 최단 거리'는 5이다.
이제 육안으로 보지않고 다익스트라 알고리즘을 사용하게 되면 매번 방문하지 않은 노드 중에서 최단 거리가 가장 짧은 노드를 선택하므로 1번 -> 3번(cost:10)의 경로를 선택하게 된다. 이처럼 음수 간선이 존재하면 최단 거리를 찾을 수 없는 상황이 발생한다.
반면에 벨만-포드 알고리즘을 사용하게 되면 매번 모든 간선을 전부 확인하므로 1번 -> 2번 -> 3번(cost:20-15=5)의 경로를 선택하여, 최단 거리를 찾을 수 있게 된다.
정리하자면,
[다익스트라 알고리즘]
-
매번 방문하지 않은 노드 중에서 최단 거리가 가장 짧은 노드를 선택하여 한 단계씩 최단 거리를 구해나간다.
-
음수 간선이 없다면 최적의 해를 찾을 수 있다. (음수 간선이 있을 때는 최적의 해를 찾을 수 X)
-
시간 복잡도가 빠르다.
(OElogV)--> 개선된 다익스트라 알고리즘 (우선순위 큐 사용)
[벨만-포드 알고리즘]
-
(정점 - 1)번의 매 단계마다 모든 간선을 전부 확인하면서 모든 노드간의 최단 거리를 구해나간다. (<-->
다익스트라와 차이점은 매 반복마다 모든 간선을 확인한다는 것이다.다익스트라는 방문하지 않은 노드 중에서 최단 거리가 가장 가까운 노드만을 방문한다.)- 다익스트라 알고리즘에서의 최적의 해를 항상 포함하게 된다.
-
음수 간선이 있어도 최적의 해를 찾을 수 있다. (음수 간선의 순환을 감지할 수 있기 때문이다.)
-
시간 복잡도가 느리다.
O(VE)
※ 모든 간선의 비용이 양수일 때는 다익스트라를, 음수 간선이 포함되어 있으면 벨만-포드를 사용하면 된다.
벨만-포드 알고리즘 수행과정
벨만-포드의 과정은 아래와 같다.
-
출발 노드를 설정한다.
-
최단 거리 테이블을 초기화한다.
-
다음의 과정을 (V(=정점) - 1)번 반복한다.
- 모든 간선 E개를 하나씩 확인한다.
- 각 간선을 거쳐 다른 노드로 가는 비용을 계산하여 최단 거리 테이블을 갱신한다.
- 만약 음수 간선 순환이 발생하는지 체크하고 싶다면 3번 과정을 한 번 더 수행한다.
--> 이때 최단 거리 테이블이 갱신된다면 음수 간선 순환이 존재하는 것이다.
음수 간선 순환을 왜 확인하는지 알아보자.
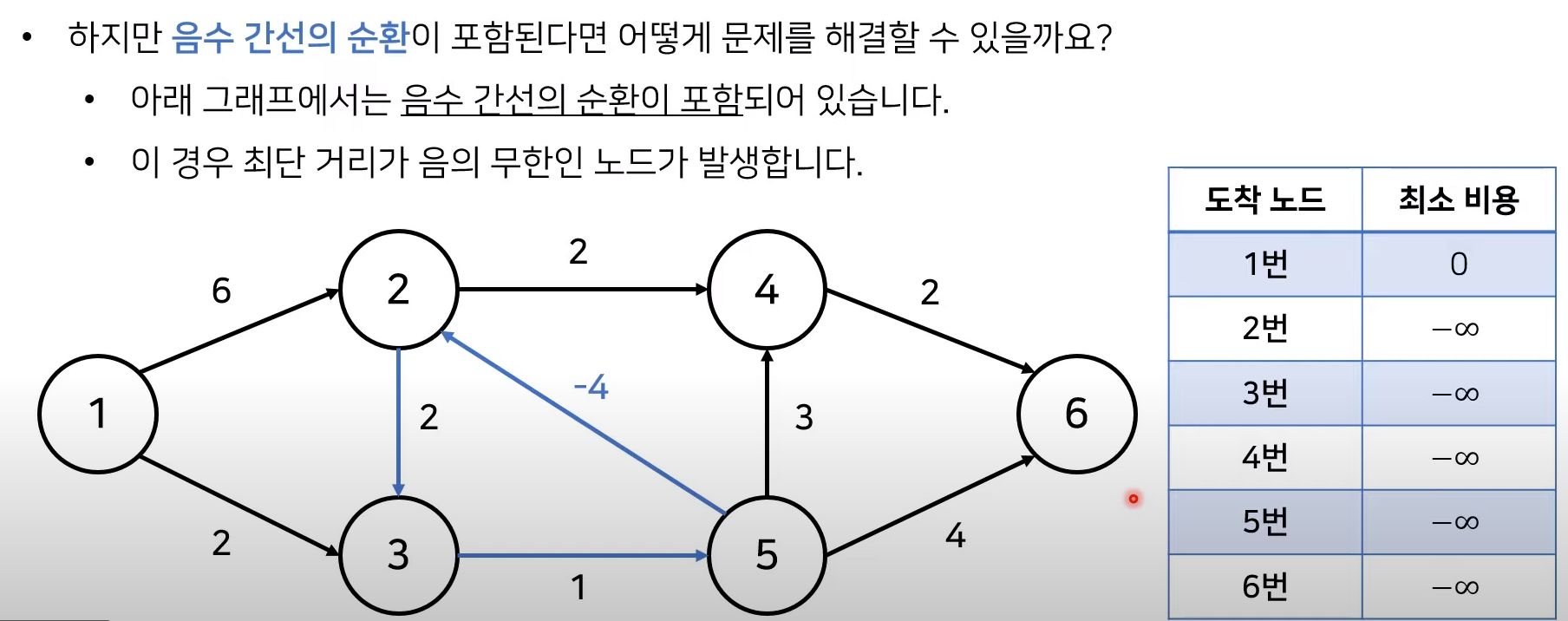
사진 출처 : 링크
그림에서 '2번, 3번, 5번 노드들' 음수 간선의 순환이 포함되어 있다. 만약 '2번 -> 5번'으로 가는 비용을 계산하면 2번 -> 3번 -> 5번(cost:2+1-4= -1)로 -1이 된다.
그러나 '2번 -> 5번'으로 가는 경로는 순환(cycle)이 있기 때문에 비용을 -1로 단정지을 수 없으며, 순환을 계속 돌게되면 '2번 -> 5번'으로 가는 비용을 무한히 줄일 수 있게 된다. 이는 1번 노드를 제외한 모든 노드에서도 비용을 무한히 줄일 수 있기 때문에 최단 거리를 구할 수 없게되므로 우리는 꼭 음수 간선 순환을 확인해주어야 한다.
V - 1까지 모든 단계를 진행한 후, 다음 단계인 V번째 단계일 때도 최단 거리 테이블이 갱신된다면 최단 거리를 무한히 줄일려는 시도이므로 음수 간선 순환이 존재한다는 사실을 알 수 있다. 따라서 V번째 단계에서 최단 거리 테이블이 갱신 여부로 음수 간선 순환을 확인할 수 있다. (V - 1까지 단계를 진행하면 모든 노드에 대한 최단 거리가 확정된다.)
벨만-포드 알고리즘 코드 (Python)
[BOJ 11657]의 정답이기도 하다.
import sys
input = sys.stdin.readline
INF = int(1e9)
# 노드의 개수, 간선의 개수를 입력
v, e = map(int, input().split())
# 모든 간선에 대한 정보를 담는 리스트 만들기
edges = []
# 최단 거리 테이블을 모두 무한으로 초기화
distance = [INF] * (v + 1)
# 모든 간선의 정보 입력
for _ in range(e):
a, b, c = map(int, input().split())
# a번 노드에서 b번 노드로 가는 비용이 c라는 의미 (a -> b 의 비용이 c)
edges.append((a, b, c))
def bellman_ford(start):
# 시작 노드에 대해서 초기화
distance[start] = 0
# 전체 v - 1번의 라운드(round)를 반복
for i in range(v):
# 매 반복마다 '모든 간선'을 확인한다.
for j in range(e):
cur_node = edges[j][0]
next_node = edges[j][1]
edge_cost = edges[j][2]
# 현재 간선을 거쳐서 다른 노드로 이동하는 거리가 더 짧은 경우
if distance[cur_node] != INF and distance[next_node] > distance[cur_node] + edge_cost:
distance[next_node] = distance[cur_node] + edge_cost
# v번째 라운드에서도 값이 갱신된다면 음수 순환이 존재
if i == v - 1:
return True
return False
# 벨만 포드 알고리즘 수행
negative_cycle = bellman_ford(1)
# 음수 순환이 존재하면 -1 출력
if negative_cycle:
print("-1")
else:
# 1번 노드를 제외한 다른 모든 노드로 가기 위한 최단 거리를 출력
for i in range(2, v + 1):
# 도달할 수 없는 경우, -1 출력
if distance[i] == INF:
print("-1")
# 도달할 수 있으면 거리 출력
else:
print(distance[i])
- 시간 복잡도는
O(VE)이다.
V번 반복에 대해서 해당 정점과 연결되어 있는 모든 간선(E)을 탐색해주기 때문에 시간 복잡도는O(V*E) = O(VE)가 된다.
참고 : https://velog.io/@qweadzs/%EC%95%8C%EA%B3%A0%EB%A6%AC%EC%A6%98-%EB%B2%A8%EB%A7%8C-%ED%8F%AC%EB%93%9C-%EC%95%8C%EA%B3%A0%EB%A6%AC%EC%A6%98
https://stalker5217.github.io/algorithm/bellman-ford/
https://ssungkang.tistory.com/entry/Algorithm-%EB%B2%A8%EB%A7%8C%ED%8F%AC%EB%93%9CBellman-Ford-%EC%95%8C%EA%B3%A0%EB%A6%AC%EC%A6%98
https://ratsgo.github.io/data%20structure&algorithm/2017/11/27/bellmanford/
https://deep-learning-study.tistory.com/587


너무 잘 정리 되어있어서 링크 좀 퍼가겠습니다!