Bernoulli - 베르누이분포

Bernoulli

베르누이 분포는 random variable의 1회 실행결과가 1과 0의 2가지 이진값으로만 이루어진 분포를 의미합니다. 1과 0을 각각 동전의 앞면과 뒷면으로 가정한다면 동전던지기는 베르누이 분포라 할 수 있습니다.
즉, 1과 0의 값을 가지므로 근본적으로 이항분포이나 단 1회의 시행이라는 점에서 차이점이 있습니다. 또한 결과 값이 1과 0의 이산 값을 가지므로 이산확률분포(discrete probability distribution)에 속합니다.
이진분류 로지스틱리그레션로 베르누이분포를 가정하고 설명할 수 있습니다.

만약 베르누이 분포의 확률시행의 결과 $x$가 1이 나올 확률을 $p$, 0이 나올 확률을 $1-p$라고 가정해봅시다.
우선 random variable $X$가 베르누이분포를 따를 때 다음과 같이 표기됩니다.

Probability Function

확률질량함수(PMF, Probability Mass Function)는 다음과 같습니다.

이를 다음과 같이 축약하여 표현할 수도 있습니다.

만약 $x$가 1일 확률 $p$를 0.3이라 가정하면 다음과 같은 pmf를 얻을 수 있습니다.

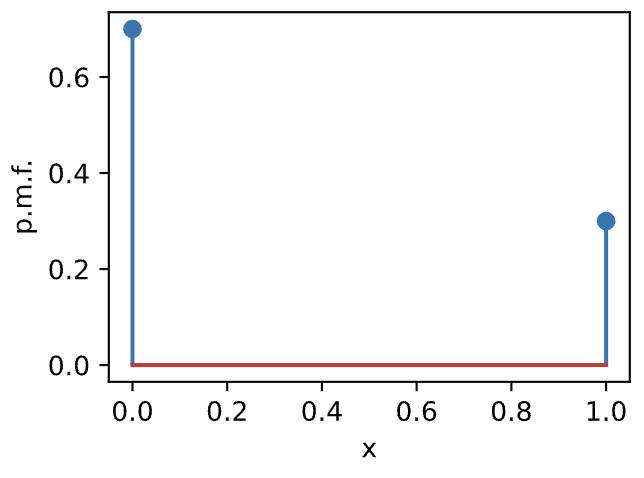
다음은 누적분포함수(CDF, Cumulative Distribution Function)를 봅시다. $x$가 0일 경우 1-p, $x$가 1일 경우 p이므로 다음과 같이 함수 $F(x)$를 표시할 수 있습니다

그리고 그래프는 다음과 같이 그려집니다.

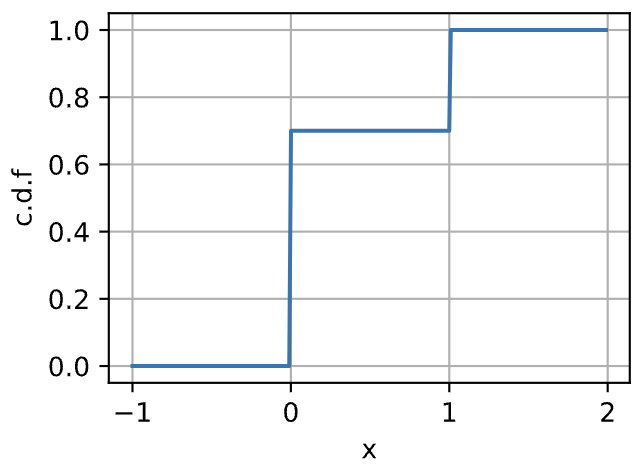
Descriptive Statistics

pmf에서 확인할 수 있듯 1일 때 $p$, 0일때 $1-p$이므로 평균은 다음과 같이 쉽게 구해집니다.

그리고 분산($\sigma^{2}$)는 다음과 같습니다.

References

[1] Zhang, A., Lipton, Z.C., Li, M. and Smola, A.J., 2021. Dive into deep learning. arXiv preprint arXiv:2106.11342.