Discrete Uniform - 이산균등분포

Discrete Uniform

이산균등분포는 각 random variable의 확률이 균등한 값으로 이루어진 것을 의미합니다.
이산 결과값으로 나오기 때문에 Discrete Uniform 이산균등분포라고 하며 이산환률분포에 속합니다.

예를 들어 다음과 같은 random variable의 집합이 있을 때, $i \in \{1, 2, 3, \ldots, n\}$ 각 항의 확률은 총 수 $n$으로 나누어준 $p_i = \frac{1}{n}$이 됩니다.

이러한 Discrete uniform distribution은 다음과 같이 씁니다.

Probability Function

먼저 PMF는 다음과 같습니다. 모든 확률변수에 대하여 균등한 확률이므로 나타날 수 있는 확률 변수의 수로 나누어준 것과 같습니다.

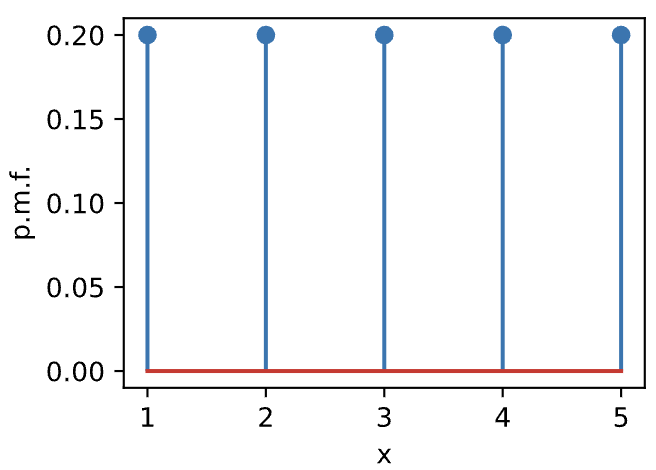
반면 CDF는 균등하게 증가하는 형태를 가질 겁니다.

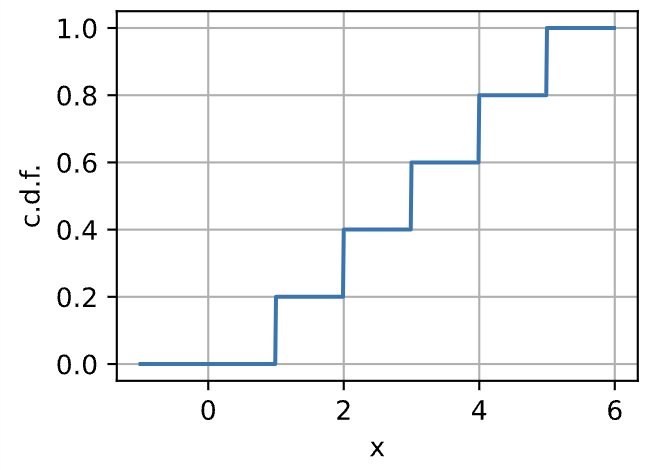
Descriptive Statistics

References

[1] Zhang, A., Lipton, Z.C., Li, M. and Smola, A.J., 2021. Dive into deep learning. arXiv preprint arXiv:2106.11342.