Backpropagation

• 이전까지 Linear classifier보다 더 강력한 Neural Network를 배움.
• Neural Network는 Linear classifier보다 강력한 성능을 가지고 있지만,
• Optimize 과정에서 Non-convex 문제 발생

Problem : How to compute gradients?

• 그렇다면 Neural Network의 gradient는 어떻게 계산?

Idea : Derive △$wL$ on paper

• 통째로 미분을 하면 중간에 값을 바꾸기도 어렵고, 많은 연산량을 필요로 하므로 bad

Idea : Computational Graphs

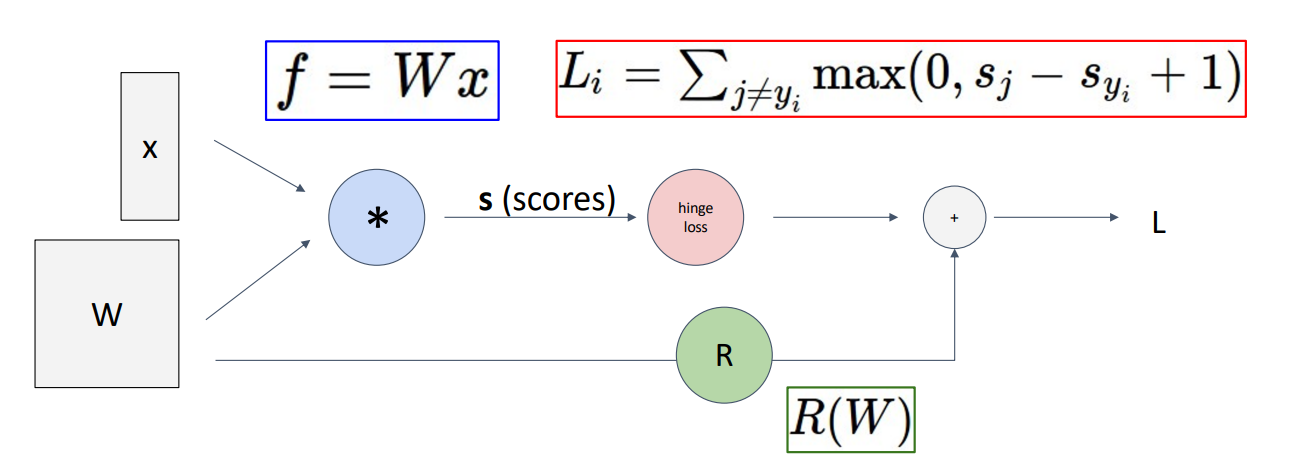
• Computational Graph는 우리의 모델이 어떻게 작동하는지를 그래프로 나타낸 것.

• 왼쪽에는 모델의 input으로 X와 학습할 수 있는 W가 node에 들어가고

• 파란색 노드에서 X와 W의 곱이 계산.

• 빨간색 노드에서는 hinge loss(SVM loss)가 계산되고

• 초록색 노드에서는 regularization을 맡아 이를 더해주어 OUTPUT L을 얻음

• 이러한 Computational Graphs는 Linear model에서는 매우 사소하고 과해보이지만

• 훨씬 더 크고 복잡한 모델에서는 효과적

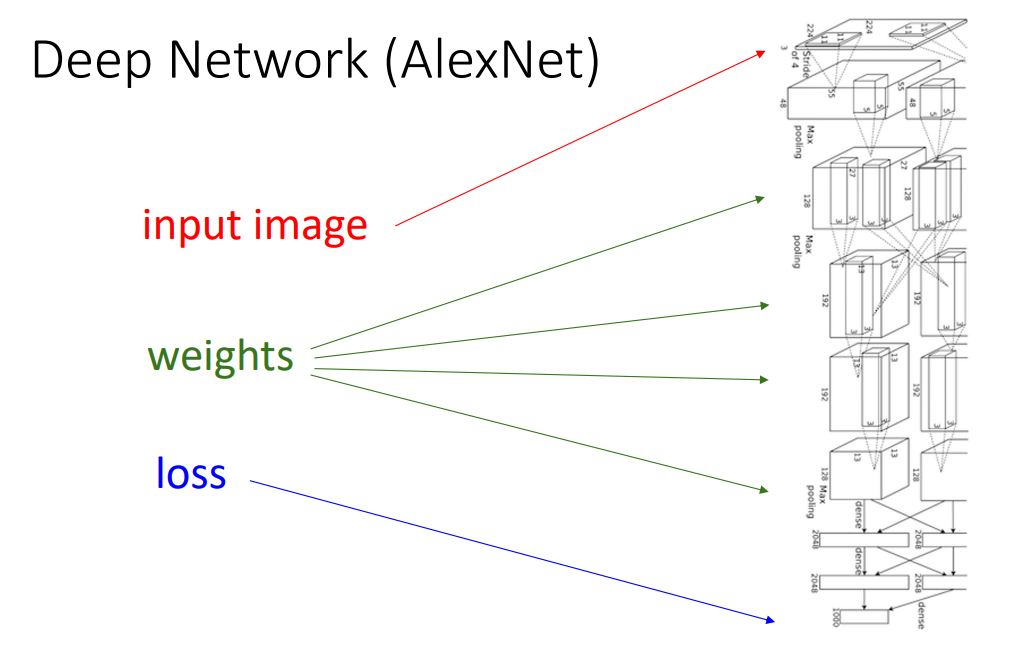
• 예를 들어서 AlexNet같은 경우에는 convolutional layer가 7개 있고, 비선형성을 가지며 모든 layer마다 regularizer와 loss function이 있음.

• 이러한 모델은 이론적으로 계산하고 싶이 않을 것이며 Computational Graph의 필요성이 커짐.

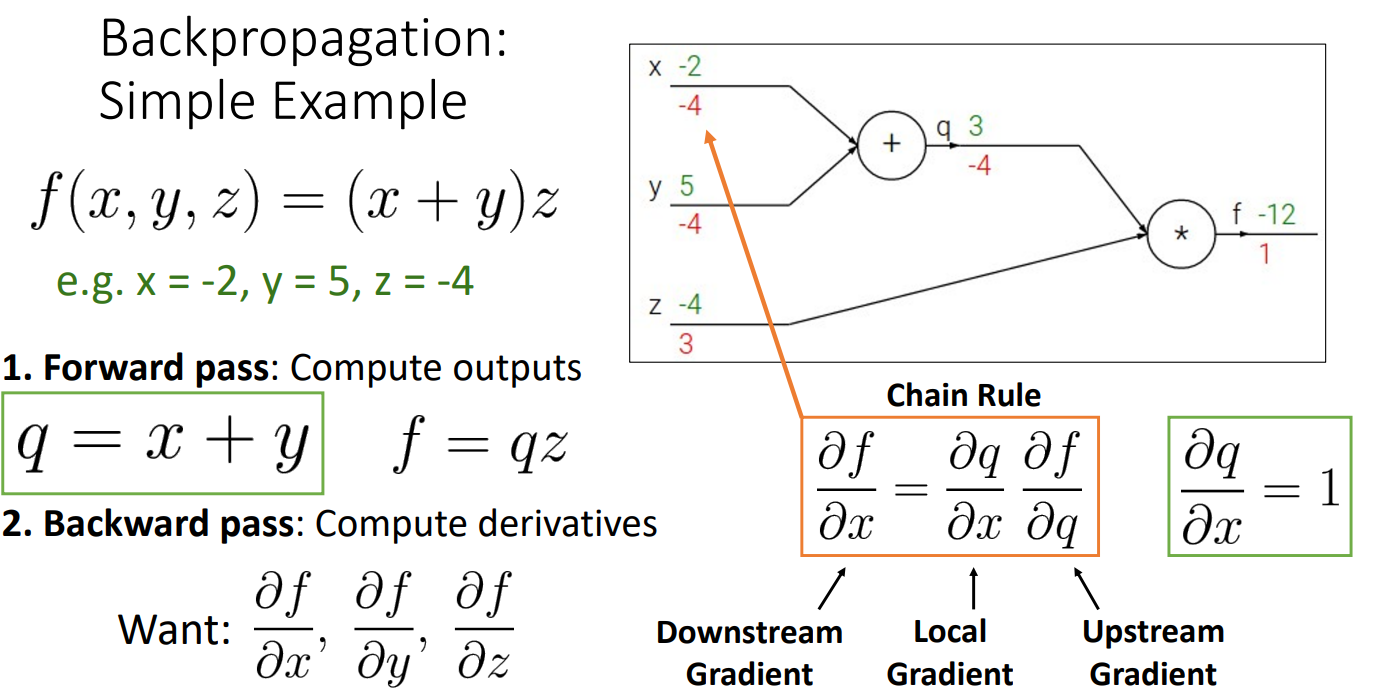
• 위와 같은 x=-2, y=5, z=-4로 이루어진 간단한 함수의 작동을 예로 들면

• gradient를 계산하기 위해서 backpropagation이 사용됨.

• 먼저 Forward pass를 통해서 computational Graph의 Output을 계산.

• Backpropagation을 통해서 우리가 얻고싶은 것은 $df \over dx$, $df \over dy$, $df \over dz$

• $df \over df$ = $1$

• $df \over dz$를 구할때 $f = qz$이므로 $df \over dz$ = $q$ = $3$

• $df \over dx$ 와 $df \over dy$를 구하기 위해서는 $f=qz$식을 이용하여 $df \over dq$ = $z$ = $-4$

• 이때 Chain Rule을 이용하여 $df \over dx$ = $df \over dq$$*$$dq \over dx$ = $-4*1$ = $-4$

• $df \over dy$ = $df \over dq$$*$$dq \over dy$ = $-4*1$ = $-4$

• 여기서 $df \over dx$를 Downstream Gradient라고 하고

• 여기서 $dq \over dx$를 local Gradient라고 하고

• 여기서 $df \over dq$를 Upstream Gradient라고 할때

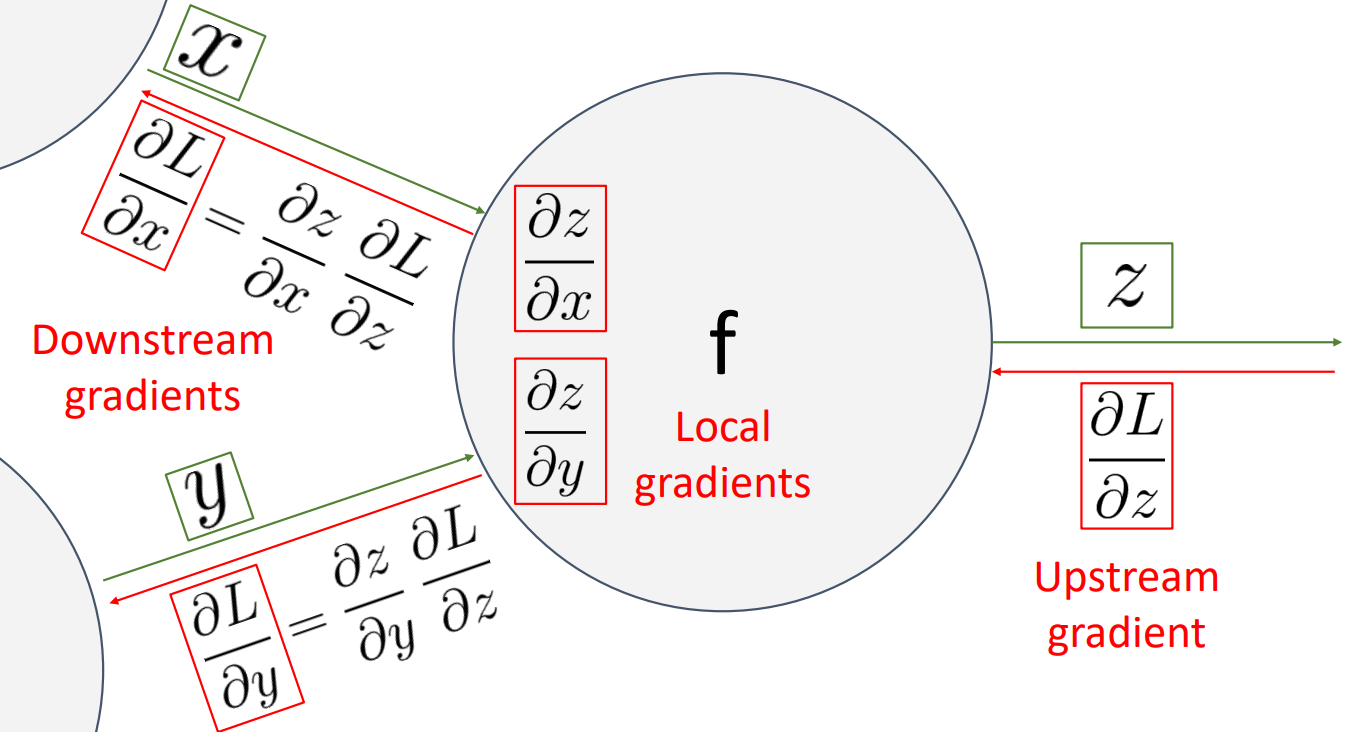
• 각 노드에서 Upstream Gradient와 Local Gradient의 곱을 통해서 Downstream을 구할 수 있음.

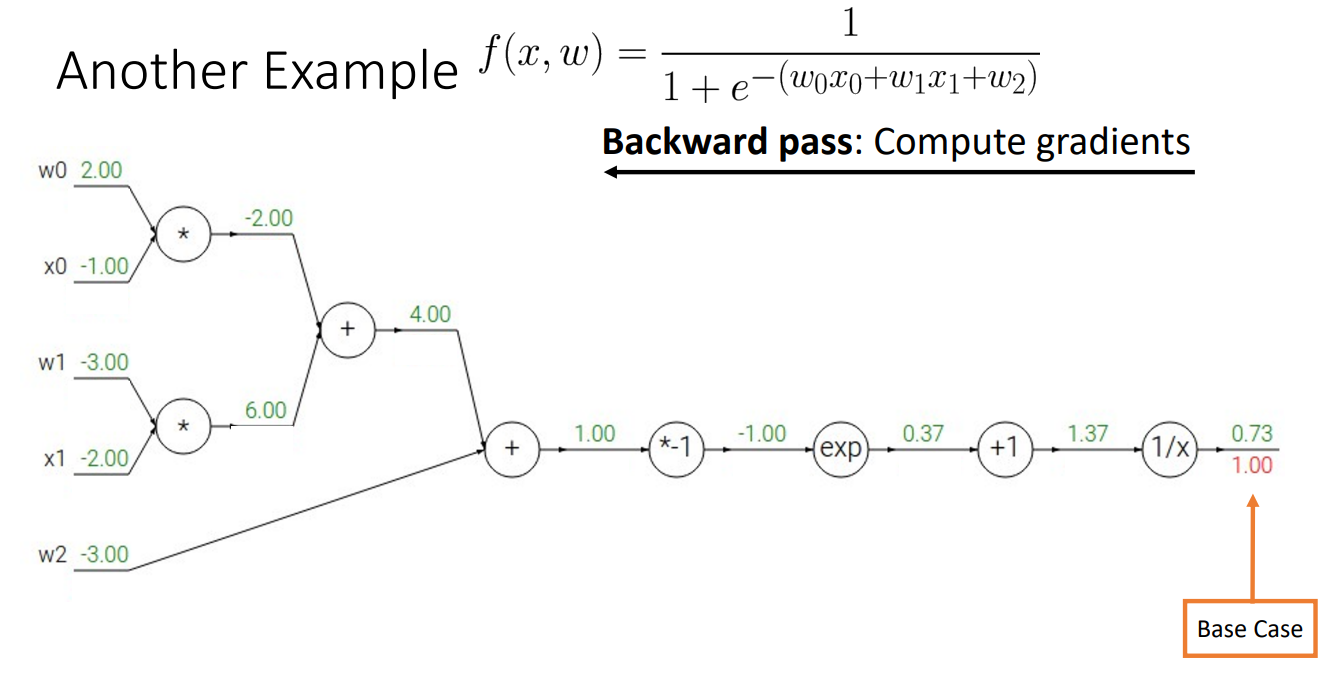
• 위의 그림을 예시로 들었을 때
  

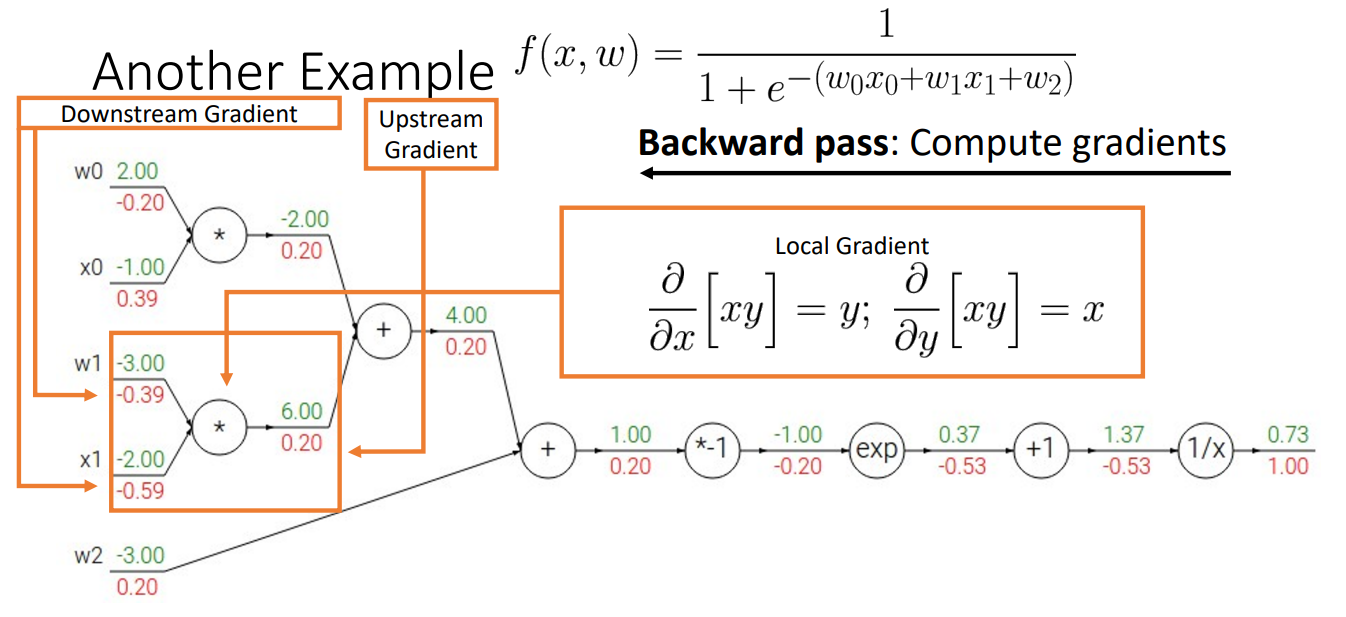
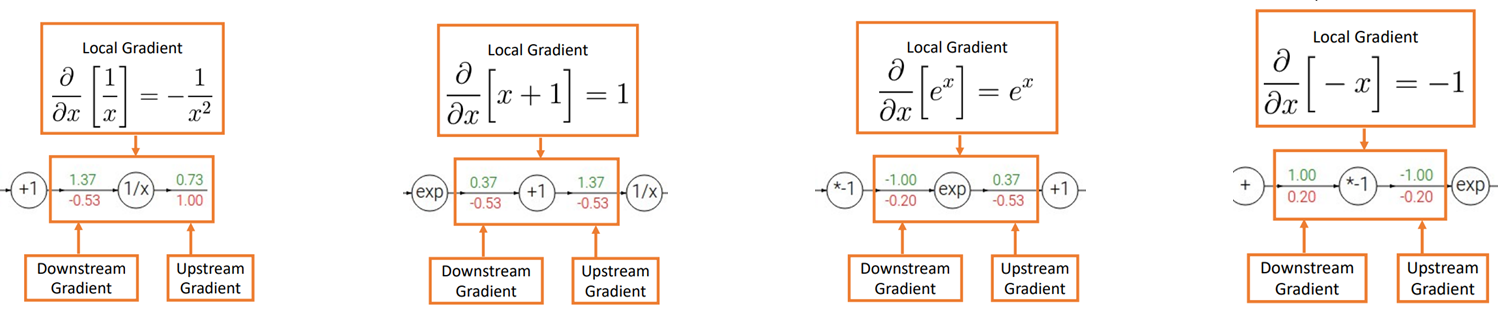
• 위와 같이 각 노드에서 Upstream Gradient와 Local Gradient를 이용하여 Downstream Gradient 계산 가능.

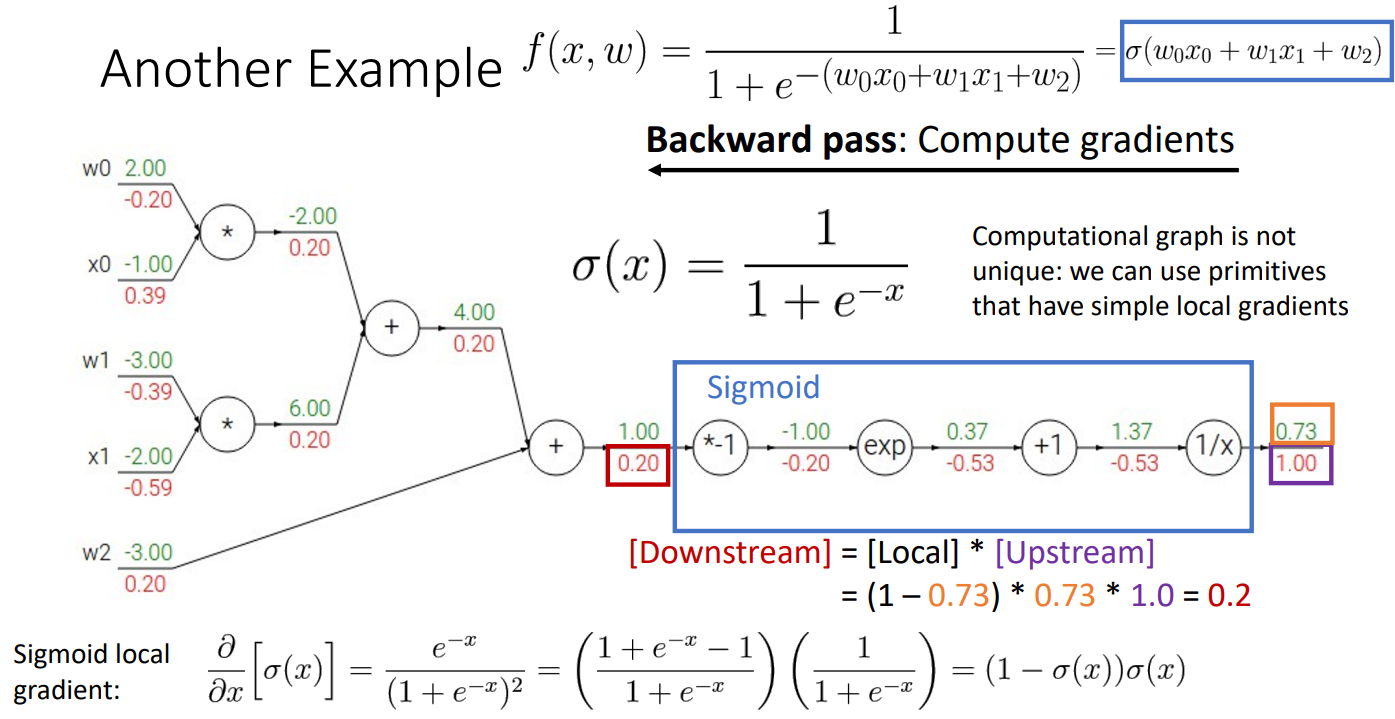
• 위의 파란색 네모박스 부분은 Sigmoid함수 부분이며 이 부분을 하나의 함수로 합쳐서 계산도 가능

• 이를 통해서 더욱 간단하게 계산이 가능

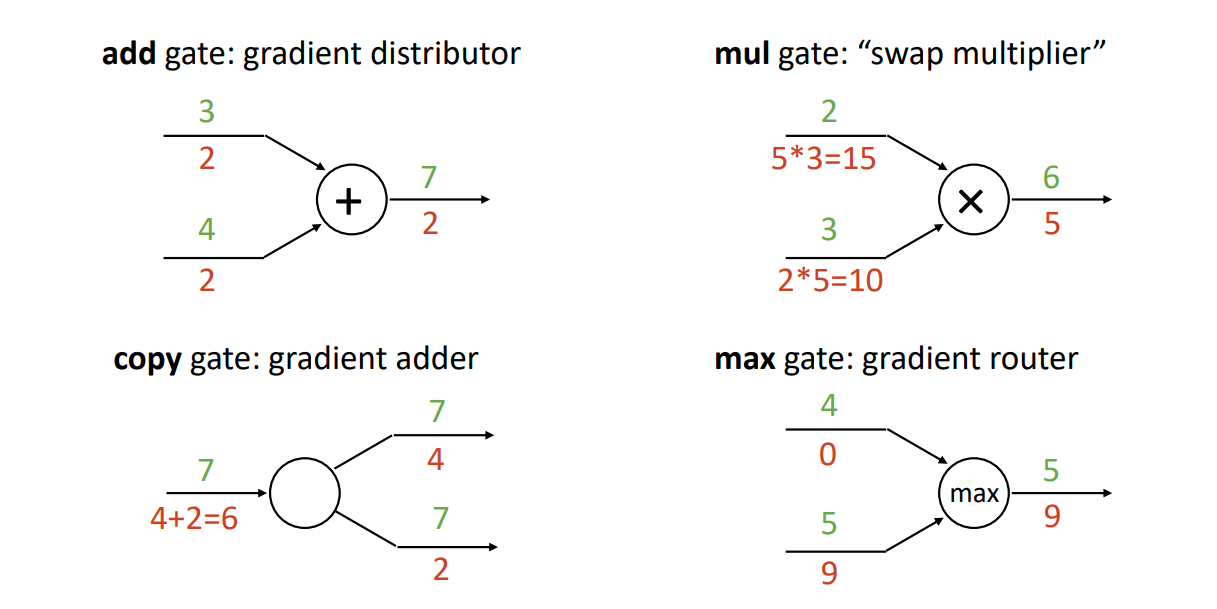
• 그리고 몇가지 패턴을 통해서 계산 없이 Downstream Gradient을 직관적으로 확인 가능

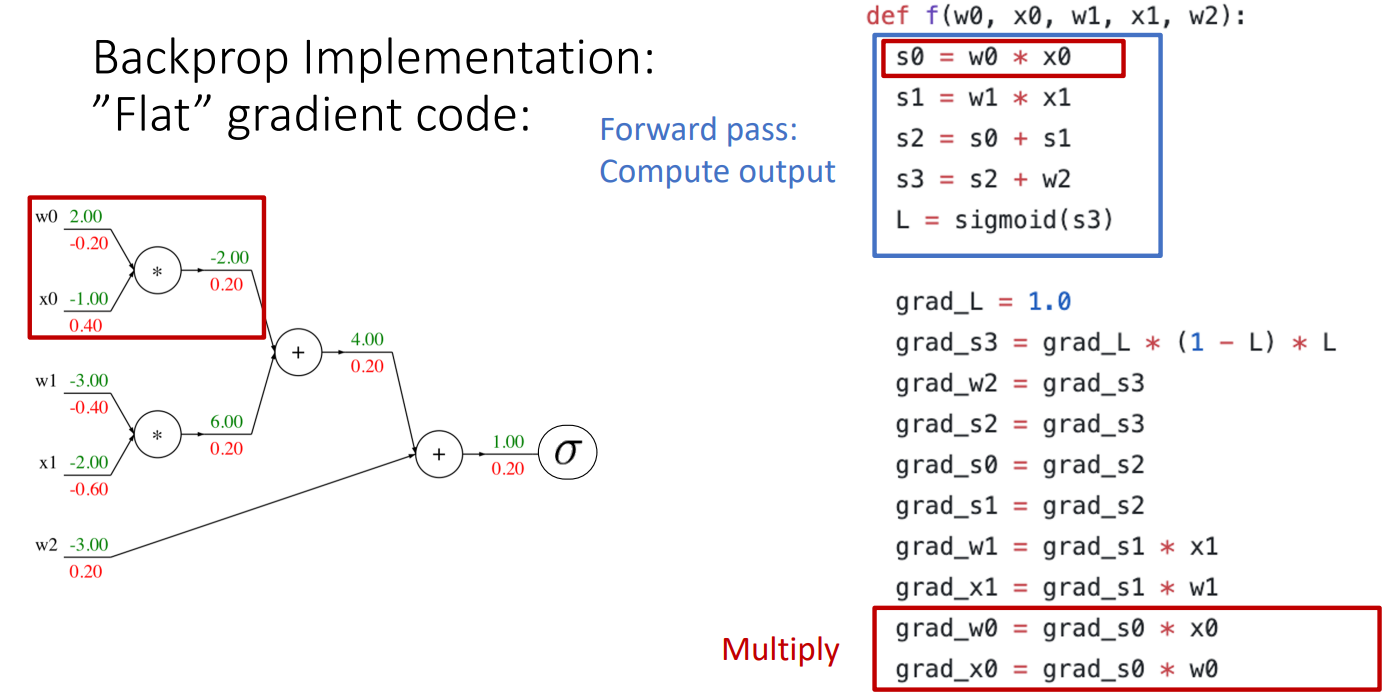
• 위의 그림에서는 곱하기, 더하기, 시그모이드 패턴을 이용하여 쉽게 gradient를 계산

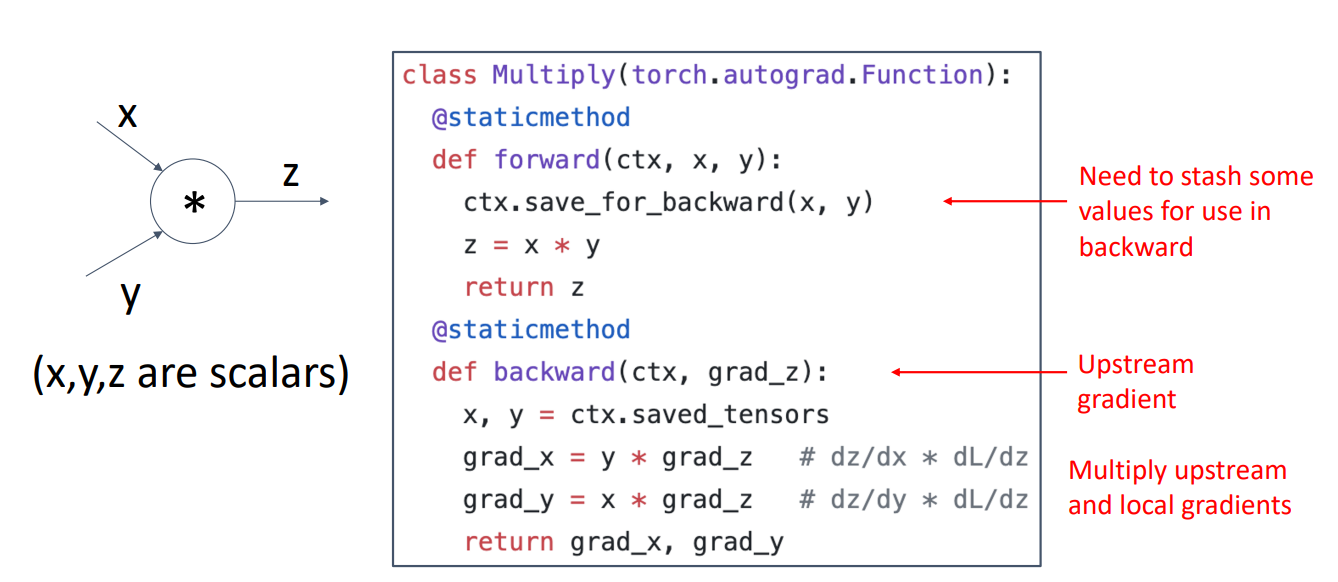
• 위와 같은 방법으로 실제 코드에서도 동작

What about vector-valued functions?

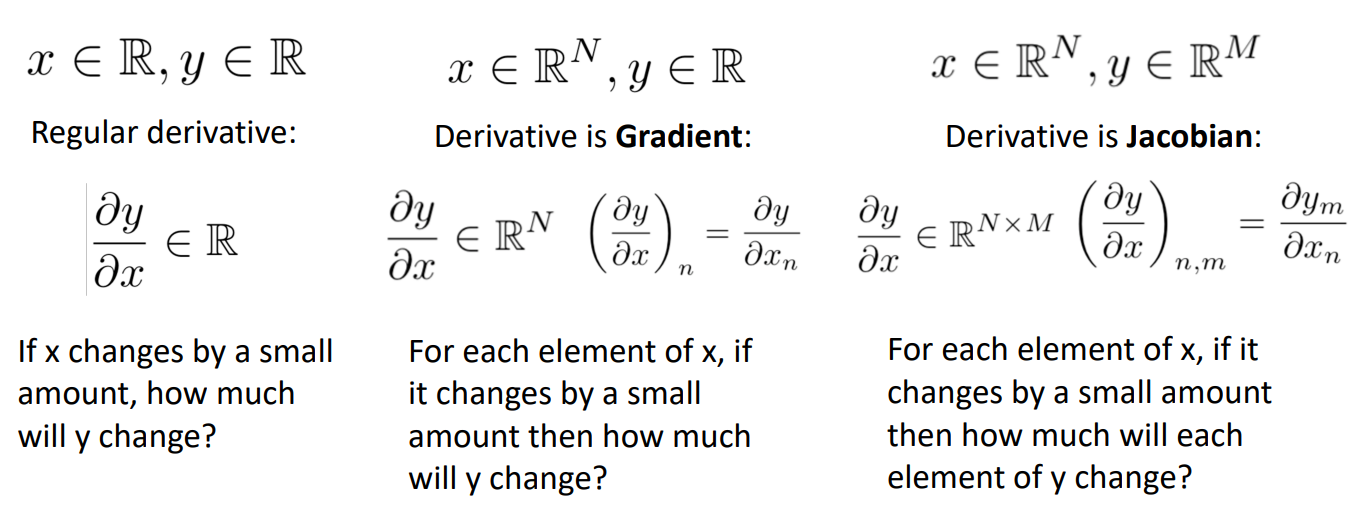
input이 scalar이고 Output이 scalar

--> 미분값: scalar 형태

input이 N차원이고 Output이 scalar

--> 미분값: N차원, Gradient로 미분

input이 N차원이고 Output이 M차원

--> 미분값 : N * M 차원, Jacobian으로 미분

• 최종 Loss는 항상 scalar 값이기 때문에 $dL \over dz$ 는 z의 차원에 해당하는 n차원을 가짐
• Local gradient는 x의 차원과 z차원의 곱인 m x n 차원을 가짐

• ReLU 함수를 예시로 보면

• Upstream gradient ( $dL \over dy$ )와 local gradient ( $dy \over dx$)의 곱을 통해서 $dL \over dx$ 계산

• 이때 실제 계산에서는 input과 output의 데이터가 매우 커서 자코비안 행렬의 sparsity가 매우 크므로 아래와 같이 나타냄

• 2차원 이상의 다차원 Tensor에서는 어떻게 계산될까?

• X,Y가 Matrices이며 Z도 Matrices일때 Loss는 마찬가지로 scalar 값을 가짐.

• Upstream gradient는 Z의 size과 같은 $D_z*M_z$로 나타남

• Local Jacobian matrices는 input과 output의 곱으로 나타남

• Downstream gradient는 input size와 같게 나타남.

• 이때 X,Y,Z는 $D_i$ X $M_i$형태이지만, 이를 vector로 flatten하여 계산을 해도 의미는 같음

• 1차원의 데이터를 가지고 자코비안 행렬을 해도 많은 연산량과 낮은 효율을 보였는데, 고차원의 데이터를 가지고 자코비안 행렬을 계산하면 더 많은 연산량과 비효율 발생

Example : Matrix Multiplication

• 위의 그림을 element-wise하게 계산해보면

• forward과정에서 $y_{1,1}$ = $x_{1,1}$$w_{1,1}$+$x_{1,2}$$w_{2,1}$+$x_{1,3}$$w_{3,1}$이므로

• $dy_{1,1}\over dx_{1,1}$ = $w_{1,1}$ 이고 이 과정을 반복하여

• $dy\over dx_{1,1}$ = $\begin{bmatrix}3&2&1&-1\\0&0&0&0\\ \end{bmatrix}$

• $dy\over dx_{1,2}$ = $\begin{bmatrix}2&1&3&2\\0&0&0&0\\ \end{bmatrix}$

• $dy\over dx_{1,3}$ = $\begin{bmatrix}3&2&1&-2\\0&0&0&0\\ \end{bmatrix}$

• $dy\over dx_{2,1}$ = $\begin{bmatrix}0&0&0&0\\3&2&1&-1\\ \end{bmatrix}$

• $dy\over dx_{2,2}$ = $\begin{bmatrix}0&0&0&0\\2&1&3&2\\ \end{bmatrix}$

• $dy\over dx_{2,3}$ = $\begin{bmatrix}0&0&0&0\\3&2&1&-2\\ \end{bmatrix}$

• 위의 행렬을 이용하여 $dL\over dx_{i,j}$ = $dL\over dy$ * $dy\over dx_{i,j}$ = $\begin{bmatrix}0&16&-9\\-24&9&30\\ \end{bmatrix}$ 계산

-위와 같이 계산

Backpropagation: Another View

• Backpropagation을 할때 Chain rule에 의하면 $dL \over dx_0$ 는 $dx_{i+1} \over dx_i$들을 곱해준 것과 동일
• 이때, $dx_{i+1} \over dx_i$ 들은 matrices이고, $dL \over dx_3$만 vector이므로 먼저 계산하여 오른쪽부터 왼쪽으로 계산하면 이 곱들을 matrices multiplication만으로 해결 가능 --> 효율적