Word2Vec

• 기존 정수 인코딩 (Integer Encoding)의 한계
  • 단어 사이의 연관성을 파악하기 어려움
• 원-핫 인코딩 (One-hot Encoding)의 한계?
  • 희소 표현을 하기에 메모리를 많이 차지 + 연관성 파악 힘듦
• 밀집 표현 (Dense Representation)
  • One-hot encoding의 희소 표현 문제를 보완
  • 벡터의 차원을 원하는 대로 설정할 수 있음
  • 데이터를 이용해서 표현을 학습

• CBOW (Continuous Bag of Words)
  • 주변 단어를 활용해 중간에 있는 단어를 예측
• Skip-Gram
  • 중간 단어를 활용해 주변에 있는 단어를 예측

CBOW - Continuouse Bag of Words

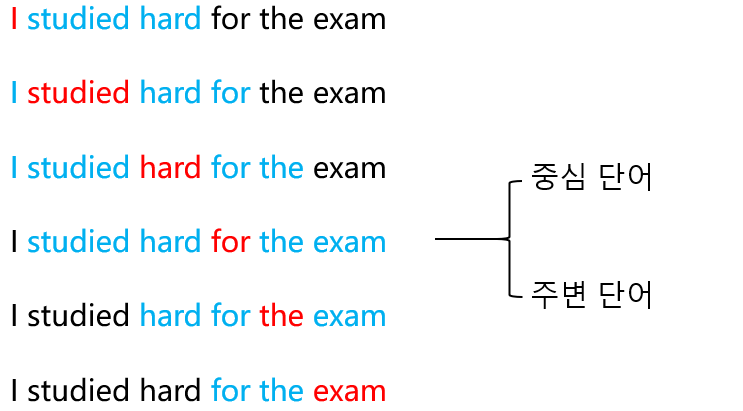
• hypterparameter로 주변 단어 개수 지정
  
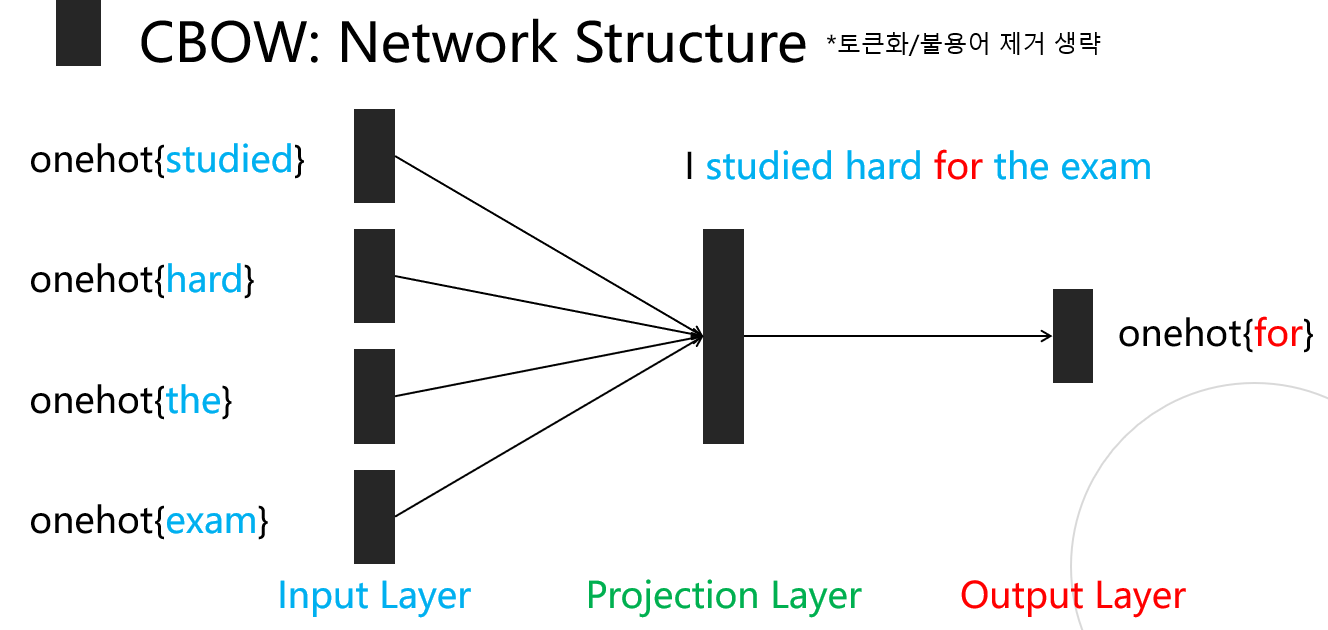
• Input : 주변 단어 개수 X 2(앞뒤) X one_hot
• output : 중심 단어 onehot
• Loss : 중심 단어 onehot과 정답 중심 단어 onehot의 $\sum C.E$
  
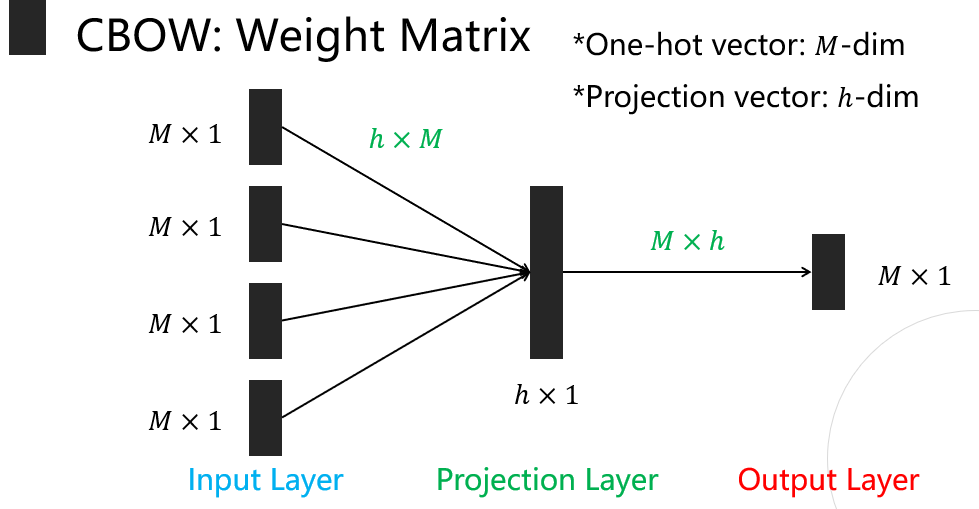
• projection layer를 중심단어의 Dense Rep으로 사용
  
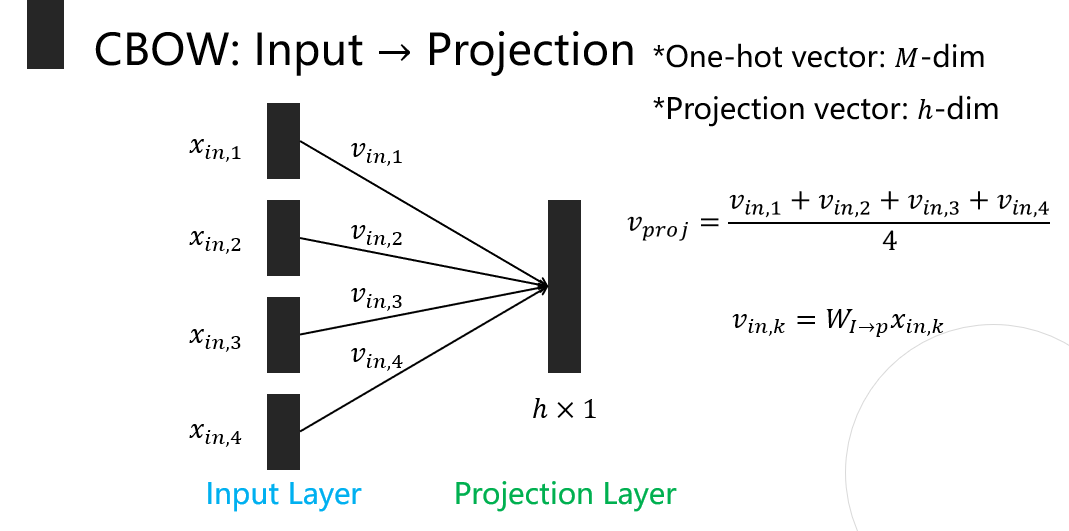
• X와 Weight Metrix의 곱을 통해 projection layer값 계산
  
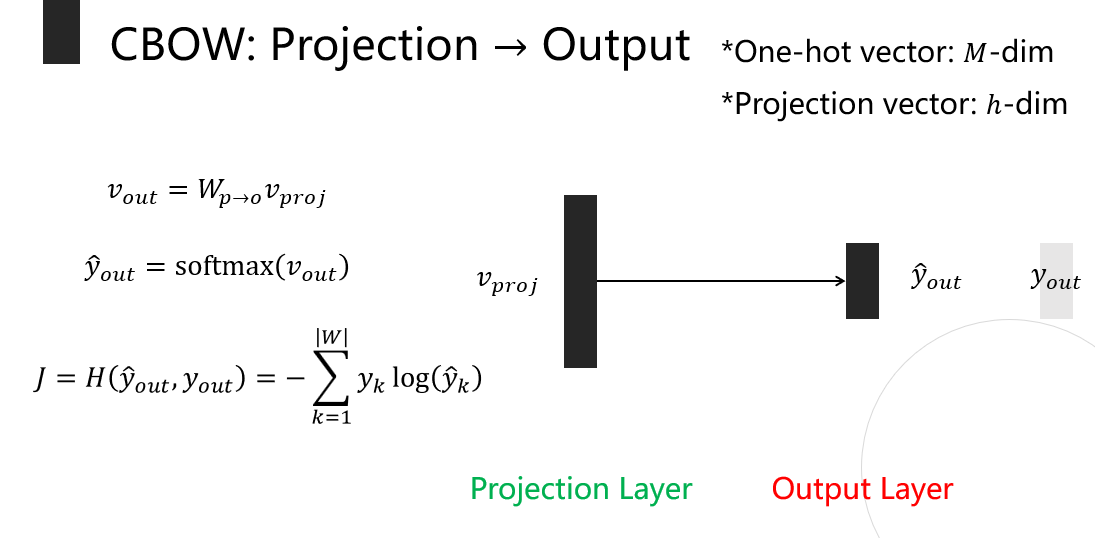
• projection layer와 weight의 곱을 통해 output 값 계산
• Output을 softmax취하고 Cross Entropy를 계산하여 Loss 계산

SkipGram - 중심에서 주변으로

• 중심 단어를 이용하여 주변 단어를 예측
  
• CBOW와 반대

NNLM : NN-Language Model

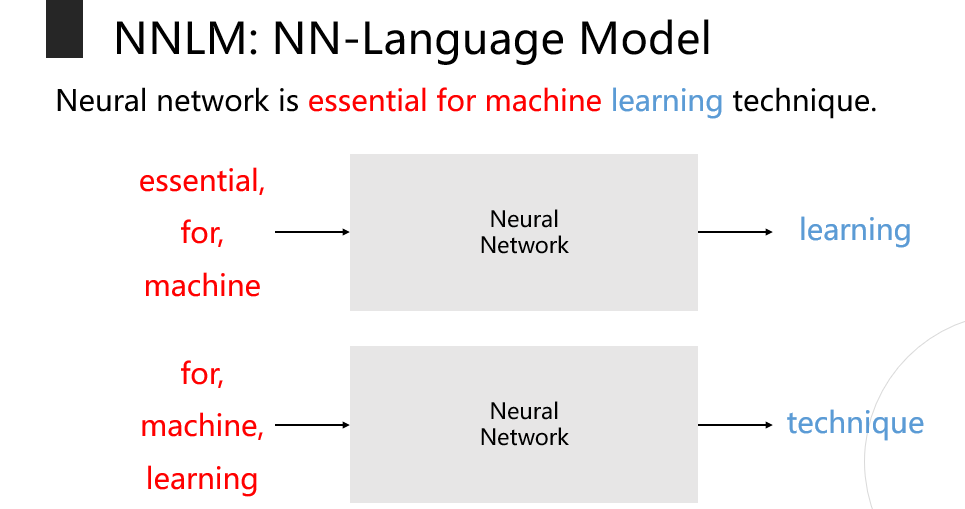
• N개의 단어를 이용하여 뒷 단어를 예측
• NNLM 모델은 정해진 길이의 과거 정보만을 참조하므로 long-term 정보를 파악할 수 없다.
• 문장의 길이가 달라질 경우 한계점이 명확하다.

SGNS: SkipGram with Negative Sampling

• Word2Vec 학습 과정에서 학습 대상의 단어와 관련이 높은 단어들에 보다 집중
• SkipGrame : 중심단어로부터 주변 단어를 예측
• SGNS : 선택된 두 단어가 중심 단어와 주변 단어 관계인가?
  
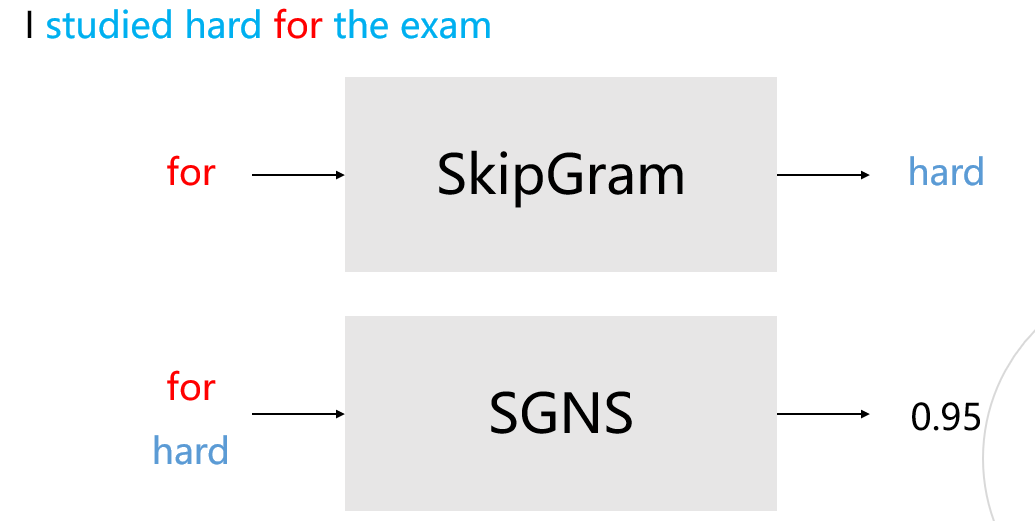
  • binary classification 문제로 바꿔서 연산량 줄어듬

Glove

Co-occurrence Matrix

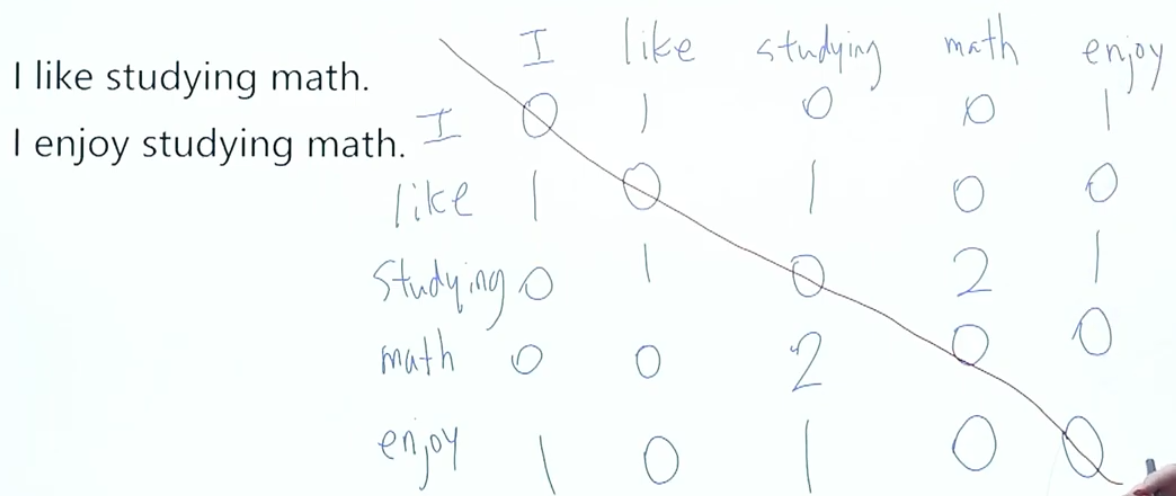
Main Idea

• 중심 단어와 주변 단어 벡터의 내적 = Corpus 동시 등장 확률
• 중심 단어와 주변 단어 벡터의 내적을 동시 등장 확률로 만들자

Nomenclature

• X: A co-occurrence Matrix
• $p(k|i) = \frac{X_{i,k}}{X_i}$ (단어i 등장시 다음 단어 k 확률)
• $w_i$ : 중심 단어의 embedding vector for word $i$
• $\hat{w_i}$ : 주변 단어의 embedding vector

Loss Function

• $f(w_i,w_j,\hat w_k)=\frac{p(i|k):주변단어가 k일때 중심단어가i일 확률}{p(j|k):주변단어가 k일때 중심단어가j일 확률}$
  $f_1((w_i-w_j),\hat w_k)=\frac{p(i|k)}{p(j|k)}$
  $f_2(\frac{(w_i)^T\hat w_k)}{(w_j)^T\hat w_k)}=\frac{p(i|k)}{p(j|k)}$
  if $f_2(x) := exp(x)$
  $w_i^T\hat w_k=logp(i|k)$

• $w_i^T\hat w_k =logp(i|k) = log(\frac{X_{ik}}{X_i})=logX_{ik}-logX_i$
  위의 식이 교환법칙이 성립하지 않으므로, bias를 더해주어야 한다.
  $w_i^T\hat w_k + b_i+\hat b_k =logX_{ik}$

• 문제 :
  (1) $logX_{ik}$값의 발산

  • 대안 : $log(1+X_{ik})$
    (2) Co-occurrence 행렬 X가 Sparse인 경우
  • 대안 : weighted prob

FastText (패스트텍스트)

• FaceBook에서 개발한 Word2Vec 알고리즘
• 단어 단위에서 더 쪼갠 "subword"의 개념을 도입
  • 글자 단위의 n-gram
  • mouse의 3-gram 표현은 = <mo, mou, ous, use, se>
  • Then, mouse = <mo + mou + ous + use + se>
• 쓰는 이유? OOV 처리에 좋음

OOV (Out-of-Vocabulary)

• 데이터셋으로 학습하는 단어의 수 : 많아봐야 수만 ~ 수십만 개
• 한 단어의 모든 단어 학습이 불가능
• 모르는 단어 (Out-of-Vocabulary, OOV)가 등장할 경우 대처?
  • Word2Vec, GloVe에서는 처리 불가능 (처리 불가 error)

Rare words

• 빈도 수가 적은 단어들은 전처리 과정에서 제외하기도 함
  • 이들은 Word2Vec 임베딩 결과도 좋지 않음
• FastText는 Type (오타)에 대해서도 강인함

사전훈련모델

• 지도학습에서 training datset이 적을 경우 underfitting 발생 가능
• 이를 해결하기 위해 사전에 훈련되어 있는 model을 가져와 사용
• CBOW, GloVe, FastText 등으로 훈련된 사전 모델들이 존재
• Pre-trained Word Embedding: Proceduer
  • [1] 사전훈련된 Word2Vec 데이터셋을 불러온다.
  • [2] 데이터셋의 특성과 자료형을 파악한다 (visulization 등)
  • [3] 원하는 Task 수행

PCA: Principal Component Analysis

• Word2Vec의 시각화를 위한 분석 방법
• 3D-world에서 이해하기:
  • 고차원의 벡터에서 저차원의 벡터로 차원 축소
  • 시각화 가능

from sklearn.decomposition import PCA
pca = PCA(n_component = 2)
pcafit = pca.fit_transform(word_vec_list)