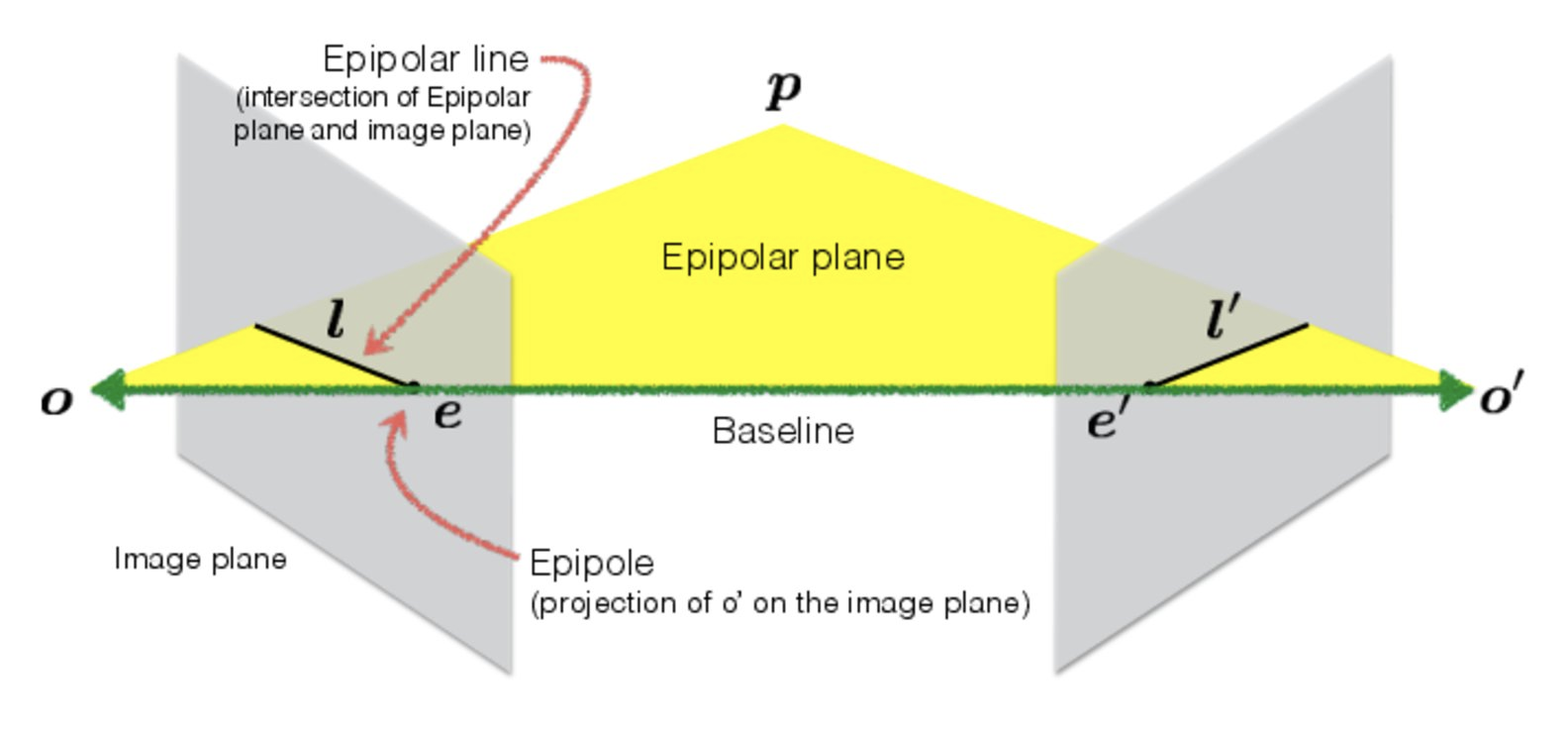
Epipolar geometry

• $p$: 3D object point
• $x,x'$: $p$가 투영되는 2개의 image plane에서의 좌표
• $o,o'$: 두 카메라의 원점
• $e,e'$: 두 카메라의 원점을 이어주는 baseline이 image plane과 만나는 점으로 Epipole이라고 정의한다.
• $l,l'$: 평면 $opo'$를 Epipolar plane이라고 부르며 이 평면이 image plane과 만나는 교선을 Epipolar line이라고 한다.

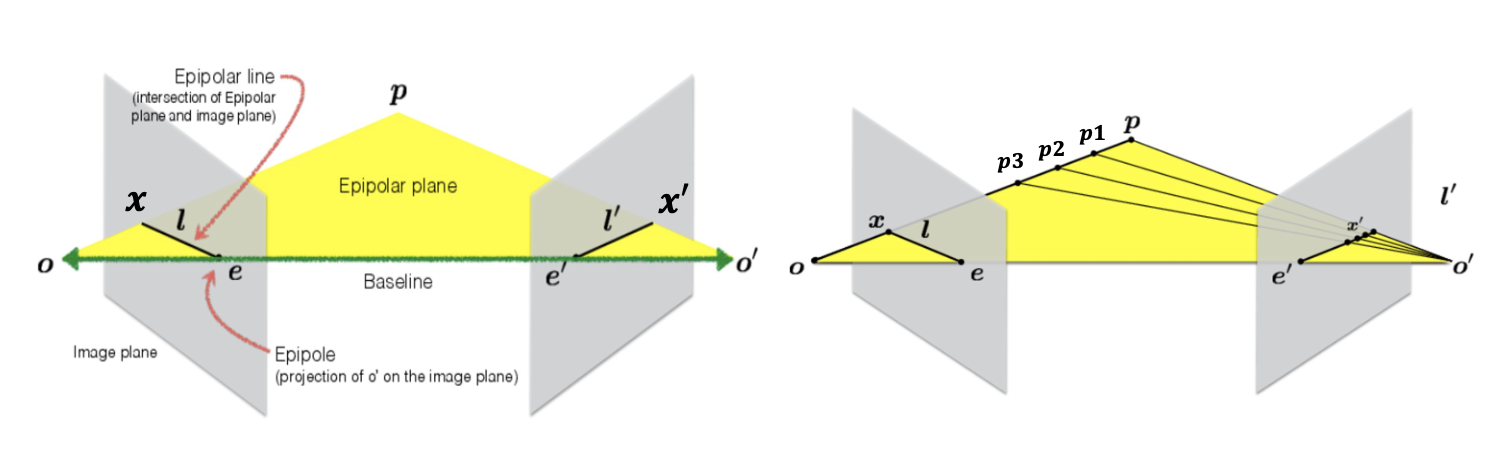
• 왼쪽 image plane에서의 좌표 $x$를 지나는 ray는 오른쪽 image plane의 epipolar line으로 투영된다.
• $p1, p2, p3$는 전부 같은 ray 상에 있어 왼쪽 image plane에는 동일한 좌표 $x$로 투영되어 depth를 알 수 없지만 오른쪽 image plane에서는 각각 다른 위치에 투영되어 depth 정보를 가질 수 있다.

Essential matrix

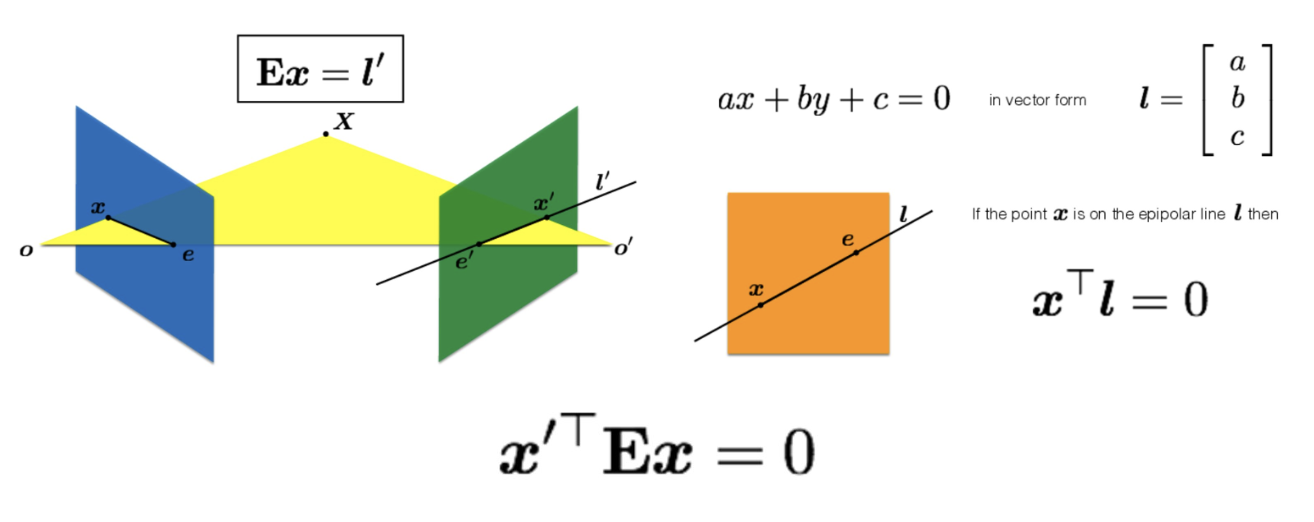
• $x$를 $l'$로 맵핑해주는 행렬을 $E$(Essential matrix)라고 하자. $E$는 point를 line으로 맵핑해준다는 점에서 point를 point로 맵핑하는 $H$(Homography)와 차이가 있다.
• 직선 $l$은 선형방정식으로 표현할 수 있으며 $l= \left[ \begin{matrix} a \\ b \\ c \end{matrix} \right]$라 할 때 직선 $l$ 위의 점 $x$에 대해서 $x^Tl=0$로 나타낼 수 있다.
• 두 식을 통해 $x'^TEx=0$이라는 식을 도출할 수 있다.(epipolar constraint)

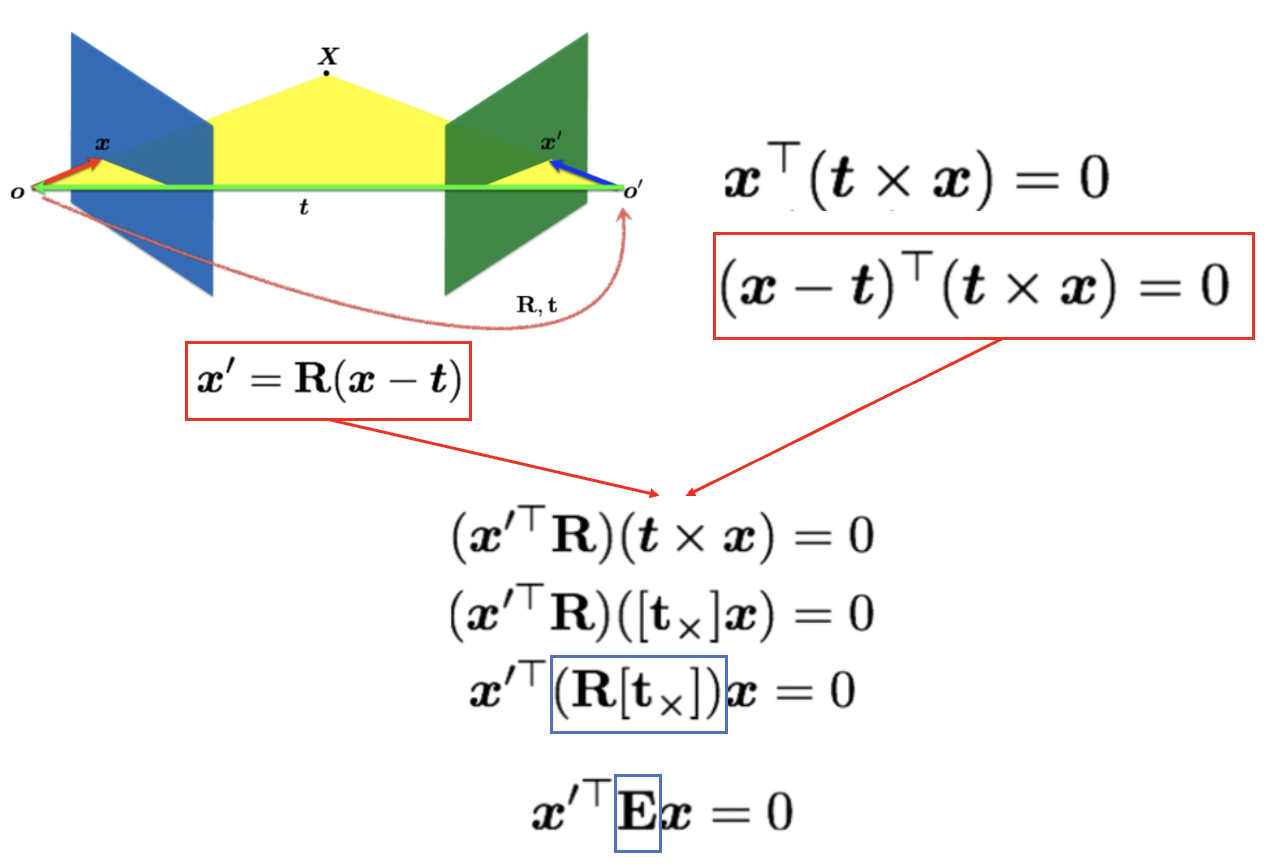
• $x$와 $x'$의 관계는 roation과 translation으로 표현할 수 있다.
• $x,t$는 동일한 평면(Epipolar plane) 상에 존재하므로 $x^T(t\times x) = 0$가 성립한다. 이러한 성질로부터 $(x-t)$도 동일 평면 상에 있으므로 $(x-t)^T(t\times x)=0$도 성립한다.(coplanar vectors)

  $t\times x$는 평면에 수직인 벡터이므로 $x^T$와 내적하면 0이 된다.

• Rigid motion과 coplanarity로부터 얻은 두 식으로부터 그림 아래의 식을 얻을 수 있으며 외적을 skew symmetric matrix로 나타내고 변환하면 $E$가 곧 $R[t_x]$임을 알 수 있다.
  

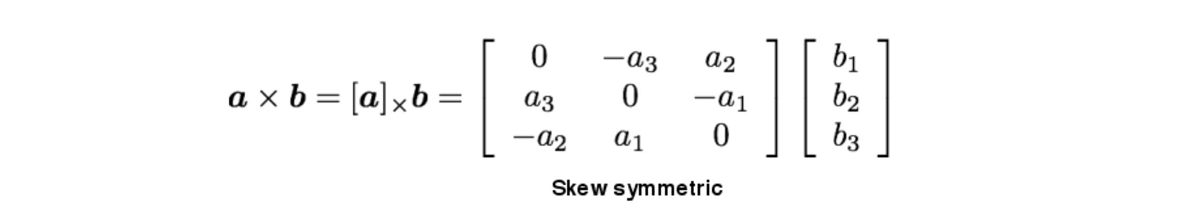
Fundamental matrix

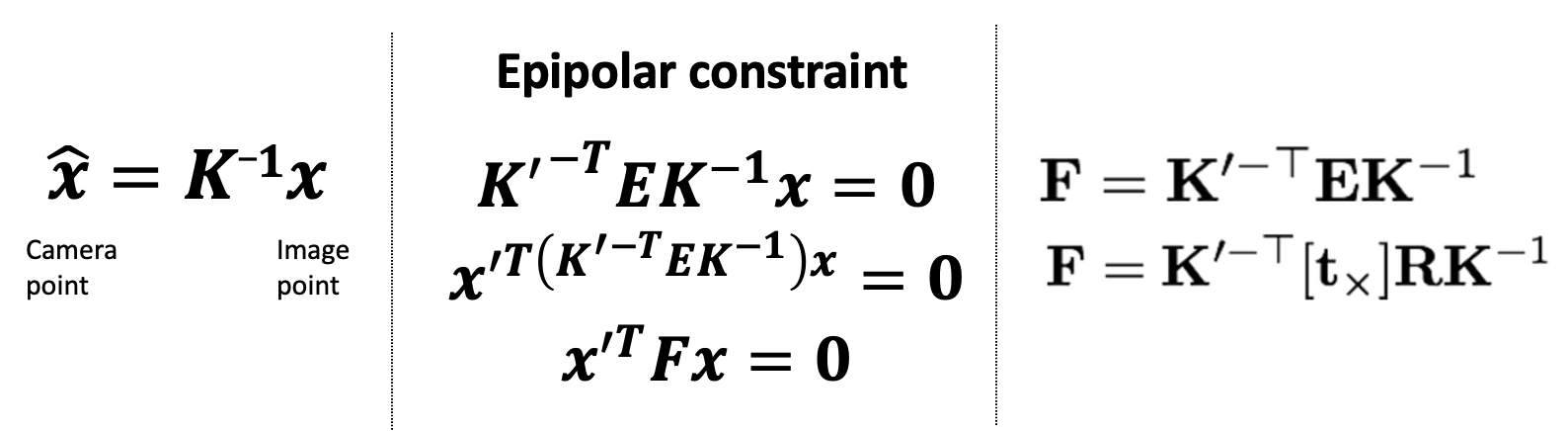
• 더 일반적인 상황으로 focal length가 1이 아닌(즉, intrinsic matrix가 $I$가 아닌) matrix
• Intrinsic matrix $K$가 camera to image 변환이었으므로 역행렬을 활용하여 $\hat{x}=K^{-1}x$를 얻을 수 있다.
• 위 식을 Epipolar constraint에 적용하면 $F = K'^{-T}EK^{-1}$임을 알 수 있고 $E$와 마찬가지로 $R$과 $t$로 표현할 수 있다.

강의

• CMU course: http://16385.courses.cs.cmu.edu/spring2021/lecture/stereogeometry