Linear algebra

Cross product

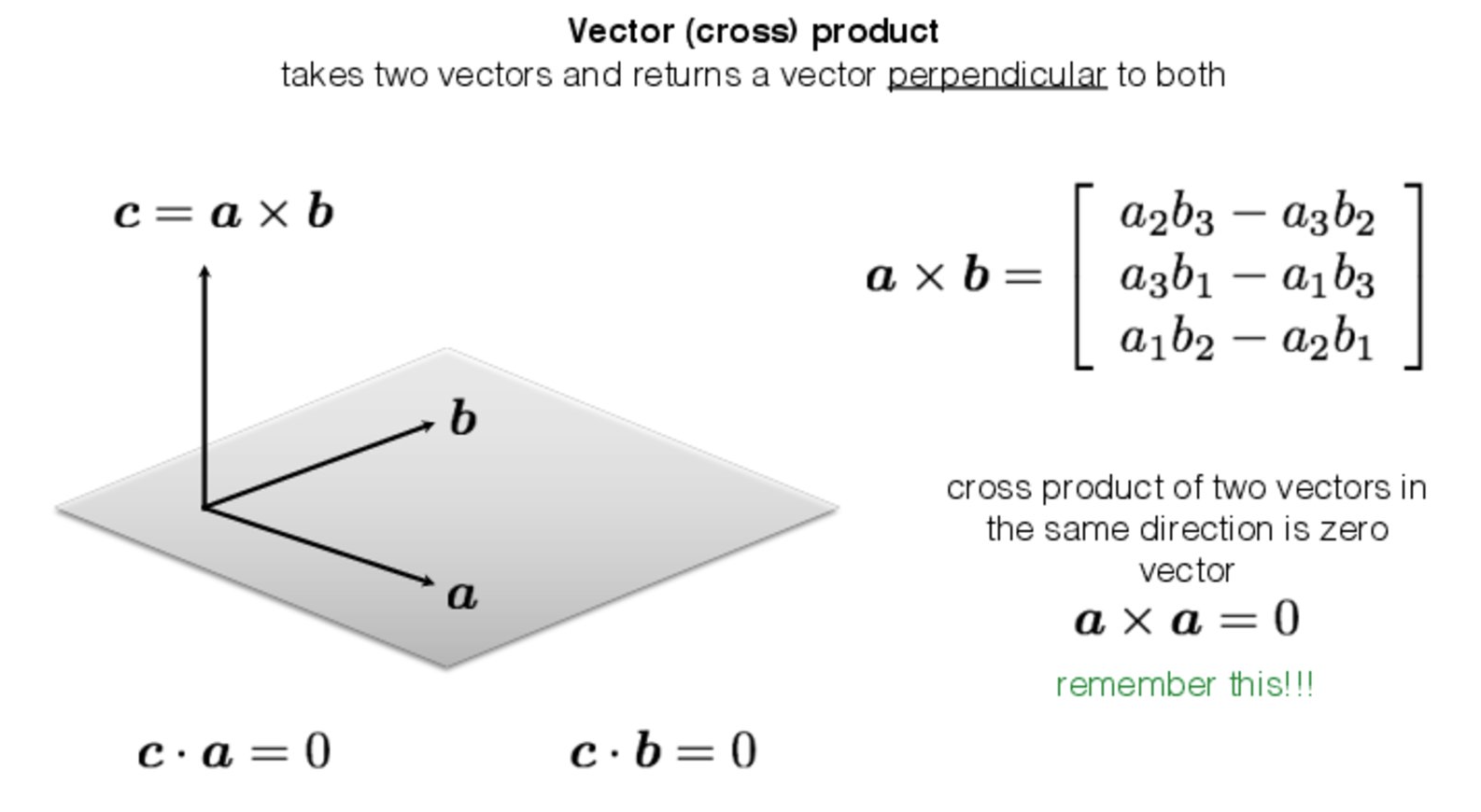
• 두 개의 독립적인 벡터 $a,b$가 있을 때 $a \times b$는 $a,b$ 모두에 직교하고 두 벡터를 포함하는 평면에 수직이다.
• 두 벡터의 방향이 같거나, 하나가 다른 하나의 마이너스 부호 혹은 둘 중 하나의 벡터의 크기가 0이라면 외적은 0이다.

Dot product

• 직교하는 두 벡터의 내적은 0이 된다.

Triangulation

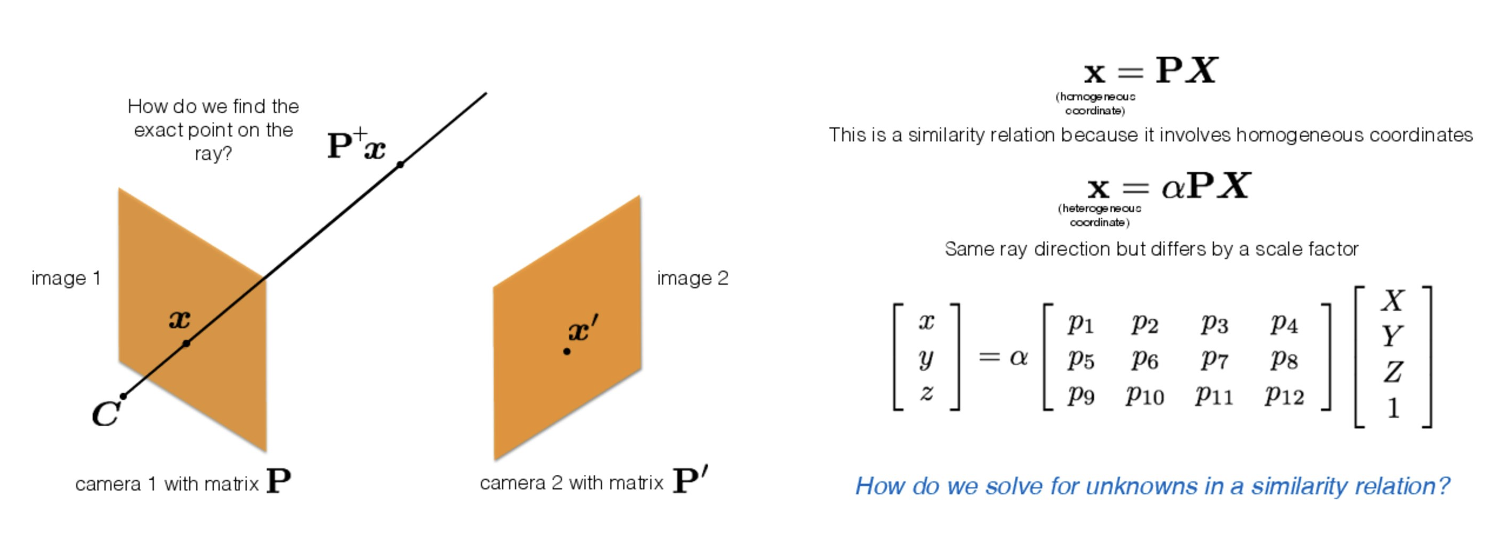
• 2D 이미지에서의 좌표 $x$를 통과하는 ray는 pseudo inverse matrix $P^+$를 곱해 표현할 수 있다.
• 이 때 homogeneous 좌표계로는 $PX$, heterogeneous 좌표계로는 $\alpha PX$로 표현할 수 있다.
• $x$는 2D image plane에서의 좌표, $X$는 3D object의 좌표를 의미한다.

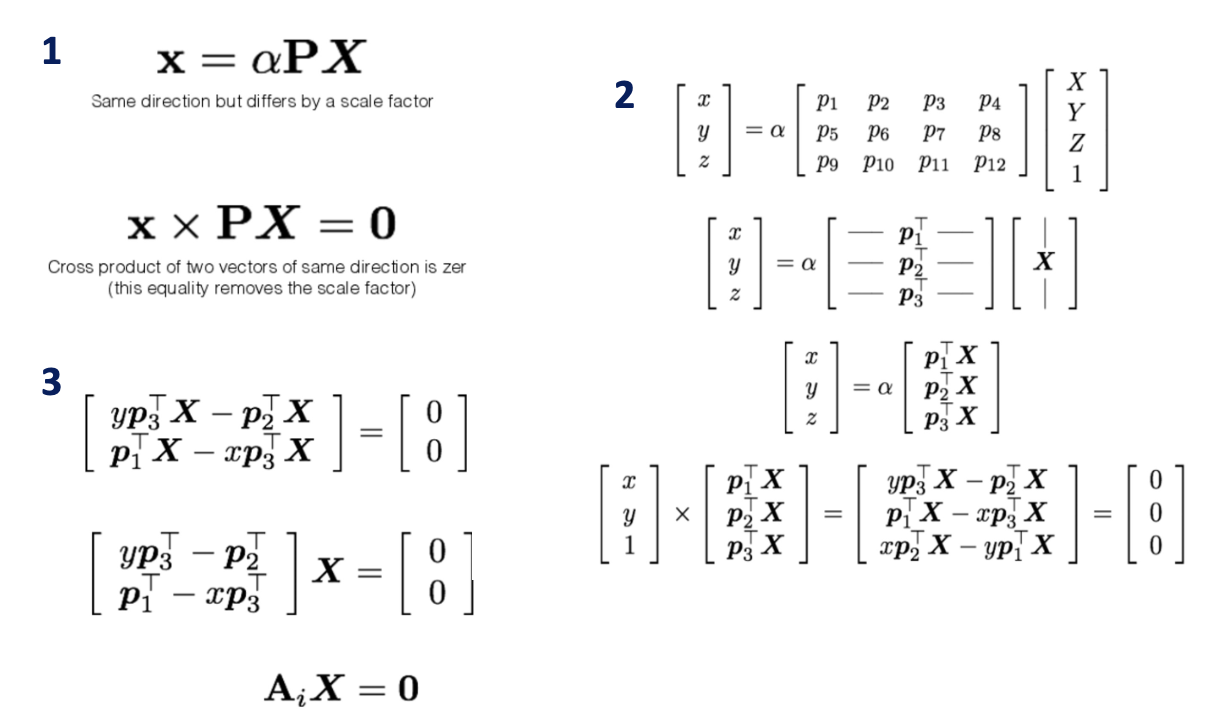
• $x$는 $\alpha$에 따라 바뀌지만 같은 ray 상에 존재하고 $PX$와 방향이 같은 벡터이므로 외적하면 0이 된다.(그림1)
• 위 성질을 이용해 그림2와 같이 식을 만들 수 있다.
• 구한 식의 3행은 1,2행의 선형결합으로 이루어져 있으므로 제외시킨다.(그림3)

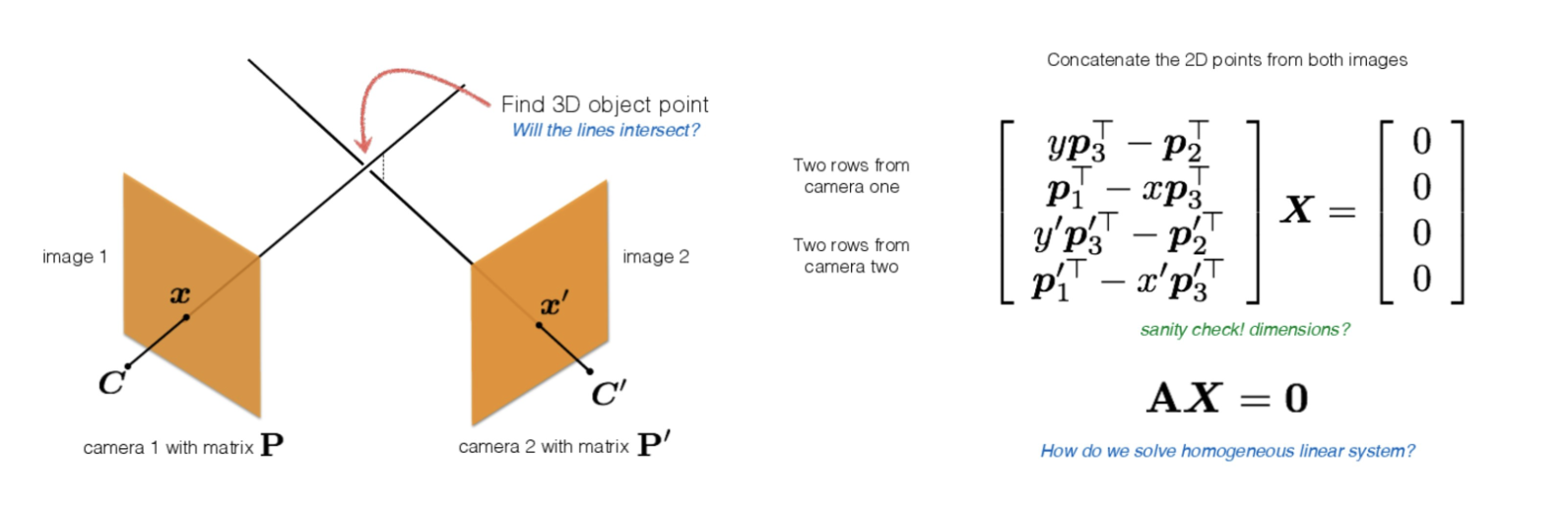
• 하나의 카메라만으로는 ray 상에 수많은 점이 존재하기 때문에 object point를 찾을 수 없다.feature
• 따라서, 두 개의 카메라 이미지에서의 correspondence feature로부터 나오는 ray가 겹치는 부분을 3D object point라고 보며 이 때 노이즈로 인해 두 ray의 차이가 생기게 되는데 이를 minimize하는 parameter를 찾는 것이 목적이 된다.
• 두 개의 카메라를 이용하므로 이전에 보았던 식을 활용하면 위 그림의 우측과 같이 $AX=0$으로 나타낼 수 있으며 SVD를 통해 식을 풀 수 있다.

강의

• CMU course: http://16385.courses.cs.cmu.edu/spring2021/lecture/stereogeometry