[논문 리뷰] Deep SORT(Simple Online and Realtime Tracking with a Deep Association Metric)

김경준·2021년 6월 19일

Paper tracking

논문

목록 보기

2/37

DeepSORT

SORT에서는 state estimation uncertainty가 낮을 때만 association metric이 정확하여 객체가 계속 스위칭 되는 현상이 있었다. 즉, occlusion에 취약했다.
Deep SORT에서는 motion과 appearance를 결합한 mertric을 이용

Track Handling and State Estimation

SORT와 동일하게 표준 칼만필터(등속 운동, 선형 관측)와 헝가리안 알고리즘을 사용하나 state space의 형태가 달라졌다.
$u$ , $v$ 는 bounding box의 center position, $γ$ 는 aspect ratio, $h$ 는 height
각 track k는 프레임마다 카운트되며 measurement와 associate 될 때마다 0으로 리셋된다.(Age)
Max age보다 오래 매칭되지 않는 track은 삭제된다.
새로운 track은 3번의 프레임까지는 잠정적 상태(Tentative)로 분류되어 매칭되지 그동안 매칭되지 않으면 즉시 삭제한다.

Assignment Problem

1. Mahalanobis distance(Short term occlusion 고려)

$d_j$ 는 $j$ 번째 bounding box detection
( $y_i$ , $S_i$ )는 $i$ 번째 track distribution에서 measurement space로의 projection
$i$ 번째 track과 j번째 bounding box detection 사이의 거리
state estimate uncertatinty를 detection이 평균 location으로부터 표준편차의 몇배 만큼이나 떨어져 있는가로 나타낸다.
inverse $χ^2$ 분포의 95% 신뢰구간만 고려하여 확률이 떨어지는 association을 배제하는 마스크
$i$ 번째 track과 j번째 detection 사이의 연관성이 인정되면 1로 평가된다.

칼만필터로 얻는 예측 상태 분포는 객체 위치에 대한 대략적인 추정치만 제공한다. 따라서, 칼만 필터만으로는 설명되지 않는 모션들이 있는데 이를 해결하기 위해 Cosine Distance 또한 도입된다.

2. Cosine distance(Long term occlusion 고려)

Bounding box detection $d_j$ 에 대해 절대값이 1인 appearance descriptor
각 track k에 대해 최신 100개의 appearance descriptor를 보관한다.
Appearance descriptor는 사전 훈련된 CNN을 통해 구한다.

$i$ 번째 track과 $j$ 번째 bounding box detection 사이의 smallest cosine distance 측정
동일한 마스크 적용

두 metrics를 가중치를 주어 합친다.
두 측정지표의 gating 영역 내에 있을 경우 연관성이 있다고 인정된다.(곱으로 계산하여 두 측정지표 gating에서 모두 1일 경우에만 통과)
실험 결과 Camera motion이 클 때 $λ$ =0로 설정하는 것이 효과가 좋았으며 이 경우 cosine distance만 사용된다.

Matching Cascade

물체가 오랫동안 가려지면 칼만필터는 uncertainty를 증가시켜 확률분포는 퍼지는 모양을 보인다.
이 때 마할라노비스 거리는 어떤 detection에 대해서도 표준편차로 계산한 거리가 작아지기 때문에 uncertainty가 높은 것을 선호.
이러한 현상은 바람직하지 못하므로 더 적은 age를 갖는(uncertainty가 작은) track에게 우선순위를 부여한다.
1. Detections와 Tracks 사이의 cost matrix 구하기
2. Detections와 Tracks 사이에서 cost를 기반으로 threshold를 적용하기 위한 mask 만들기
3. match matrix 초기화
4. unmatched detections에 대한 matrix를 Detections로 초기화(매칭 시 제거)
5. 모든 age에 대해 for문
  6. 마지막 n개 프레임에서 detection과 associate 되지 않은(age=n인) track들을 부분집합 $T_n$ 로 설정
  7. $T_n$ 의 track과 매칭되지 않은 detection $U$ 사이의 최소 cost 매칭
  8. mask의 threshold 적용 후 match matrix에 넣기
  9. 조건에 따라 unmatched matrix 제외

위 과정을 거친 후 age==1인 unmatched and unconfirmed tracks와 unmatched detection 사이의 IoU association 적용.
-> 갑작스러운 appearance change를 구하는데 도움을 준다.

++ Mahalanobis distance

평균과의 거리가 표준편차의 몇 배인지를 나타내는 값
수치적으로 얼마나 일어나기 힘들고, 이상한 값인지를 나타낸다

위 그림에서 일반적인 거리의 개념(유클리디안)으로 보면 a가 μ에 더 가깝다.

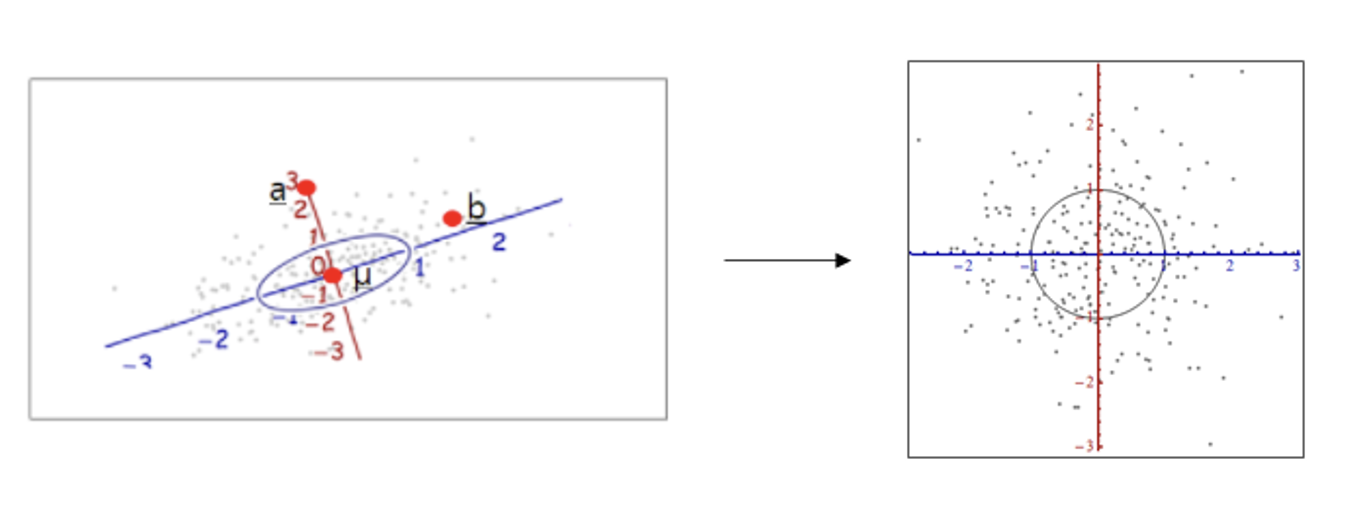
하지만 데이터들의 평균을 중심으로 데이터의 분산이 가장 큰 방향으로 하나, 그 축에 수직으로 하나 두개의 축을 잡고 표준편차를 이용하여 점의 약 68%는 한 단위 내에, 약 95%는 두 단위 내에 분포하도록 설정한 후 다시 거리를 살펴보면 a는 2.x, b는 1.x로 b가 더 가까움을 확인할 수 있다. 즉, b가 유클리디안 거리 상으로는 멀지만 더 일어날 확률이 높다.

References

김경준

이전 포스트