GAN(Generative Adversarial Networks)
Main idea
- 위조 지폐범(Generator)와 경찰(Discriminator)의 대결
- G는 최대한 진짜 같은 모조품을 만들며, D는 진품과 모조품을 구별한다.
- 경쟁적 학습을 통해 결국 완전한 모조품을 만드는 것이 목표(위조 지폐범의 승리)
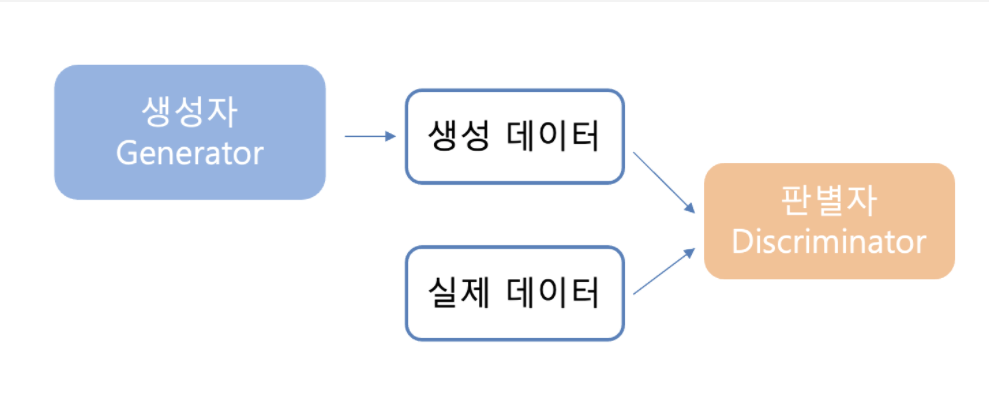
GAN은 실존하지는 않지만 있을법한 이미지를 만들어내기 위한 모델로 게임이론의 minmax 알고리즘으로부터 아이디어를 따왔다고 한다. 위조지폐범은 경찰에게 걸리면 더 진짜 같은 위조지폐를 만들려하고 경찰은 위조지폐범을 잡기 위한 기술을 또 만들어내며 서로 발전하게 되는데 이러한 모습 때문에 적대적(Adversarial)이라고 표현한다. 현실과는 달리 이 모델에서는 위조지폐범의 승리를 목표로 하며 결국 경찰이 진짜와 가짜를 분간할 수 없는 지폐(생성 이미지)를 만들어내게 된다.
Loss function
GAN의 손실함수는 다음과 같다.
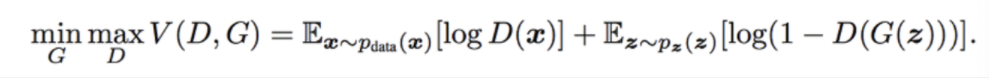
식이 다소 복잡하니 하나하나 뜯어서 해석해보자. 우변은 다음과 같이 해석할 수 있다.
- : 실제 이미지의 데이터 분포에서 하나를 샘플링하여 판별자에 넣었을 때 나온 값의 로그값의 기댓값
- : noise 벡터 분포에서 하나를 샘플링()하여 만든 생성이미지를 판별자에 넣었을 때 나온 값의 로그값의 기댓값
판별자 입장에서는 는 진짜(1)로 판별하고 는 가짜(0)로 판별하여야 하므로 우변을 최대화하는 방향으로 학습하게 된다.
생성자 입장에서는 가 를 1로 판별하게 만들고싶으므로 우변을 최소화하는 방향으로 학습하게 된다.
Optimality
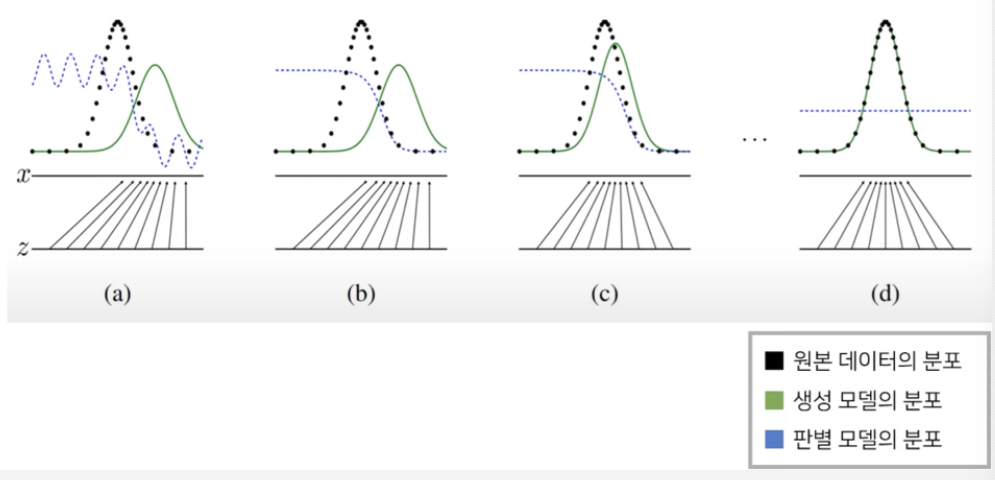
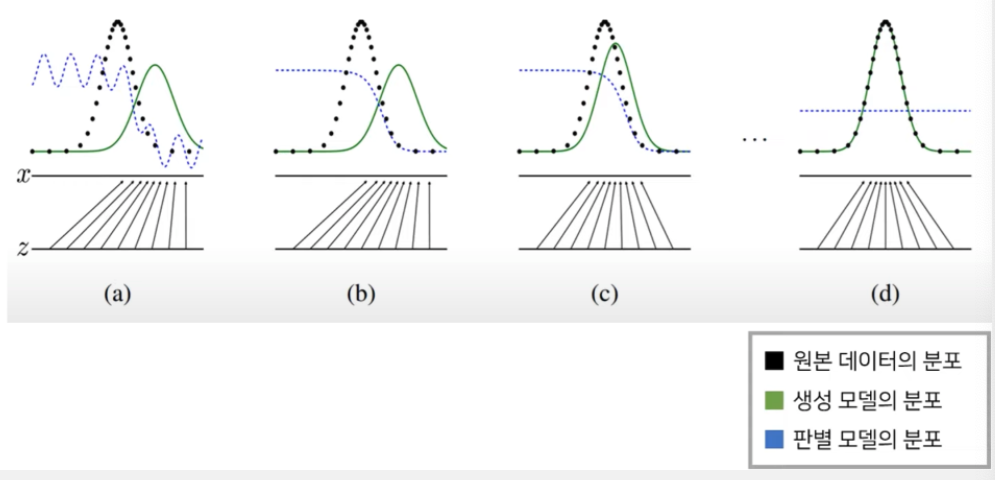
위 그림은 생성자가 학습을 통해 원본데이터로 수렴하면서 목표를 달성하는 모습을 보여준다. 생성 모델의 분포인 초록선은 원본 데이터의 분포인 검정선과 같아지도록 점점 변하며 파란선은 판별 모델의 분포를 의미한다. 학습이 전혀 안 된 상태(a)에서는 불안정한 모습을 보이다가 점차 원본 데이터는 1에 가깝게 생성 데이터는 0에 가깝에 분류하기 시작했고 최종적으로는 1/2로 수렴하게 된다. 판별자에게 1/2이라는 값은 두가지로 분류하는데 있어 가장 애매하다는 의미라는 것을 쉽게 받아들일 수 있을 것이다.
GAN의 Global Optimum point는 G가 고정되어 있을 때 = 이며 인데 이 두 조건이 만족할 때 는 1/2로 수렴한다. 이 식을 도출하는 자세한 증명과정은 아래 링크의 강의에서 볼 수 있다.
https://www.youtube.com/watch?v=AVvlDmhHgC4&t=1777s
VAE
VAE vs AE
VAE의 구조를 보면 Autoencoder와 굉장히 유사하여 둘의 차이가 극명함에도 불구하고 처음에는 이를 이해하기가 쉽지 않다. 간단히 말하자면 이 둘은 애초에 목적이 다르다. AE는 차원축소가 목적이다. input으로부터 벡터를 얻어내고자 하므로 인코더가 핵심이다. PCA와 같은 역할을 한다고 보면 된다. 반면, VAE는 GAN과 같은 생성모델이다. 이미지를 생성하기 위한 값이 필요한데 이를 추정하기 위해 인코더를 붙이는 AE와 같은 구조를 갖게되었을 뿐이라고 생각하면 된다.
- AE: 차원축소가 목적, Encoder가 핵심
- VAE: 이미지 생성이 목적, Decoder가 핵심
Structure
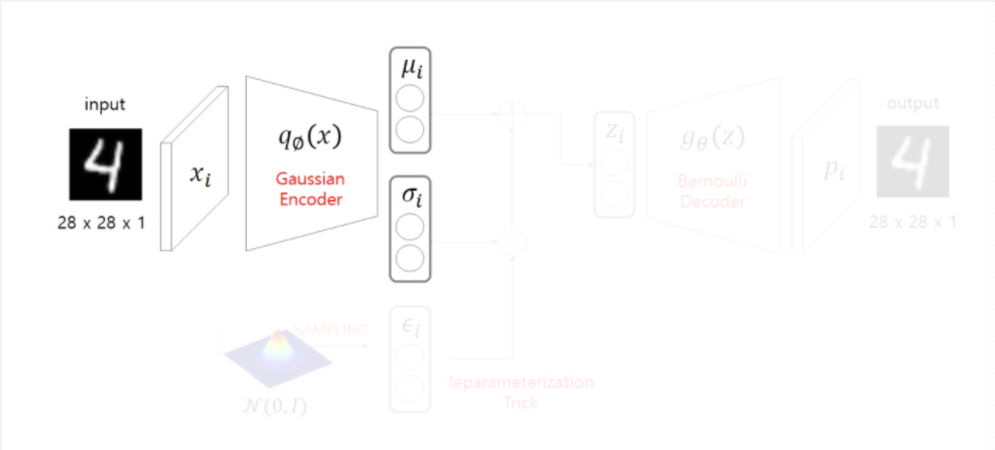
- Encoder는 가우시안 분포를 따른다고 가정하여 평균과 표준편차로 이루어진 정규분포에서 를 샘플링한다.
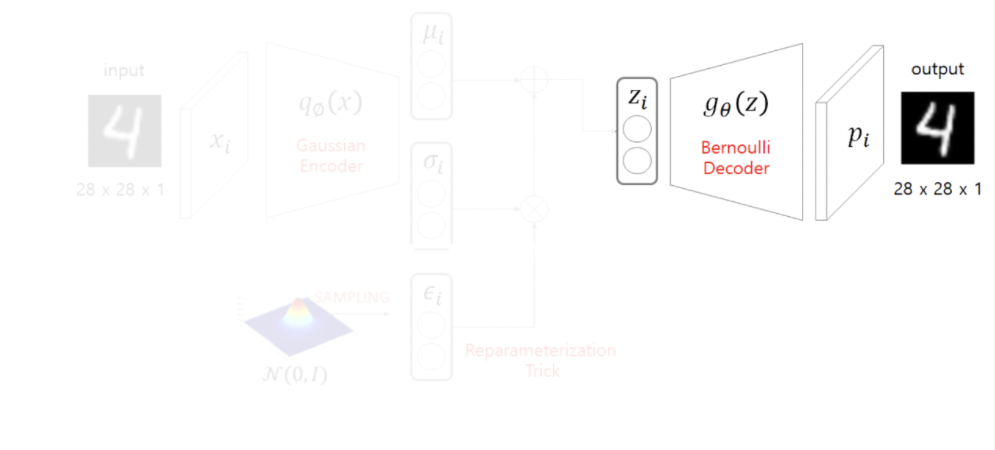
- 베르누이 분포를 따른다고 가정한 Decoder를 통해 이미지를 복원한다. 이 때, 문제점이 한가지 있는데 학습 시 역전파를 위한 미분을 할 방법이 없다는 것이다. 그리하여 중간에 한 가지의 절차를 더해준다.
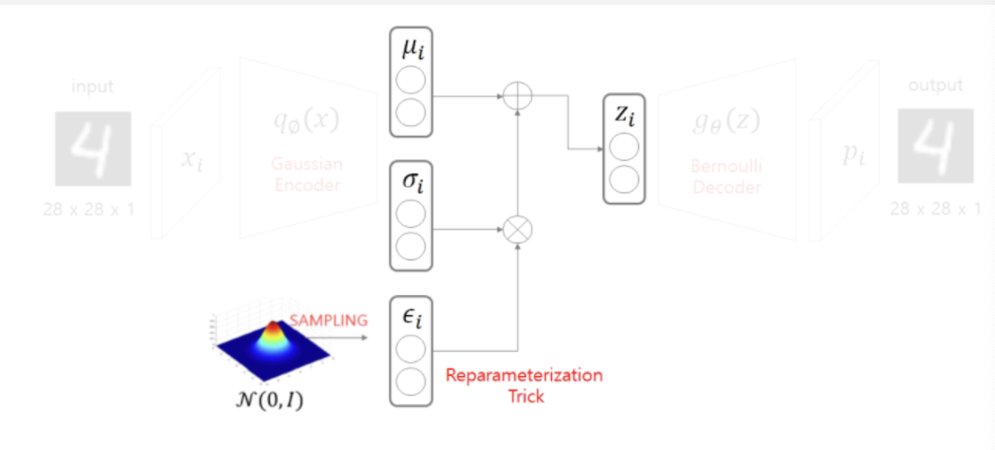
- 표준정규로부터 아주 작은 값인 epsilon을 샘플링 하여 표준편차를 곱하고 평균을 더한 값을 라 한다.(𝜇+𝜀∙𝜎)
이를 Reparameterization Trick이라고 부른다.
Loss function
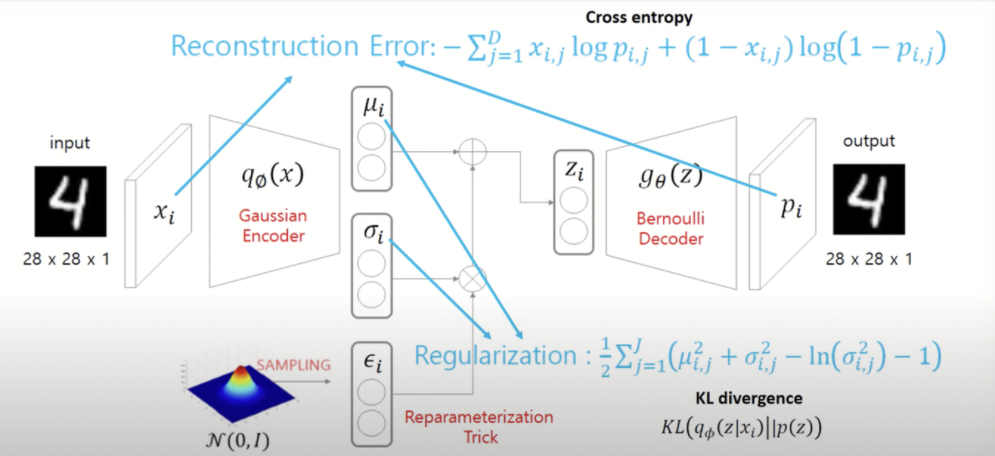
VAE의 loss function은 두 가지로 구성된다.
- Reconstruction Error: output과 input의 이미지의 차이를 최소화시킨다 -> cross entropy.
- Regularization Error: Encoder를 통과한 값의 분포와 정규분포의 차이를 최소화시킨다 -> KL divergence.
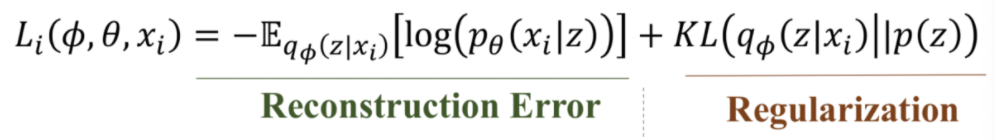
DCGAN
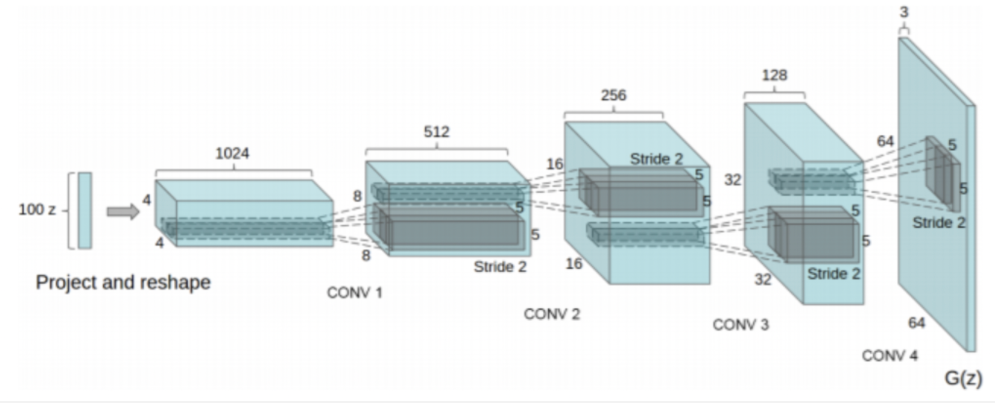
Features
- CNN의 기법을 활용 -> fully connected 구조 대신 convolution, pooling, padding 활용
- 모든 layer에 batch-normalization 적용
- Generator에서는 모든 활성화함수를 Relu를 쓰되, 마지막 출력층에서만 Tanh
- Discriminator에서는 모든 활성화 함수로 LeakyRelu 사용
Results
- Walking in the latent space

GAN에 대한 문제점 중 하나가 이미지를 생성하는 것이 아니라 수많은 데이터로 인해 기억을 해서 변형시키는 것 아니냐라는 의문에 해답을 내놓지 못했다는 것인데 DCGAN이 이 부분을 해소시켜주었다. 위 그림의 마지막 줄을 보면 input인 값에 미세하게 변화를 주자 서서히 창문이 생기는 모습을 볼 수 있는데 이로 인해 GAN이 이미지를 기억하는 것이 아니라 생성하는 것이다라는 증명을 보일 수 있었다.
- Applying arithmetic in the input space
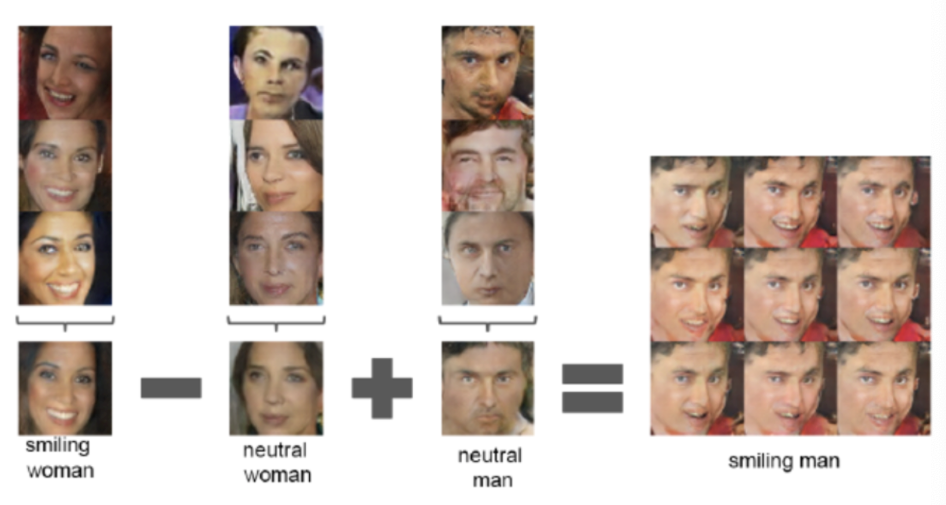
latent vector의 연산이 가능하다는 점도 DCGAN의 흥미로운 결과 중 하나였다. 위 그림을 보면 (웃는 여성 - 여성 +남성)이라는 연산을 통해 웃는 남성이 나오는 결과를 볼 수 있다.
LSGAN
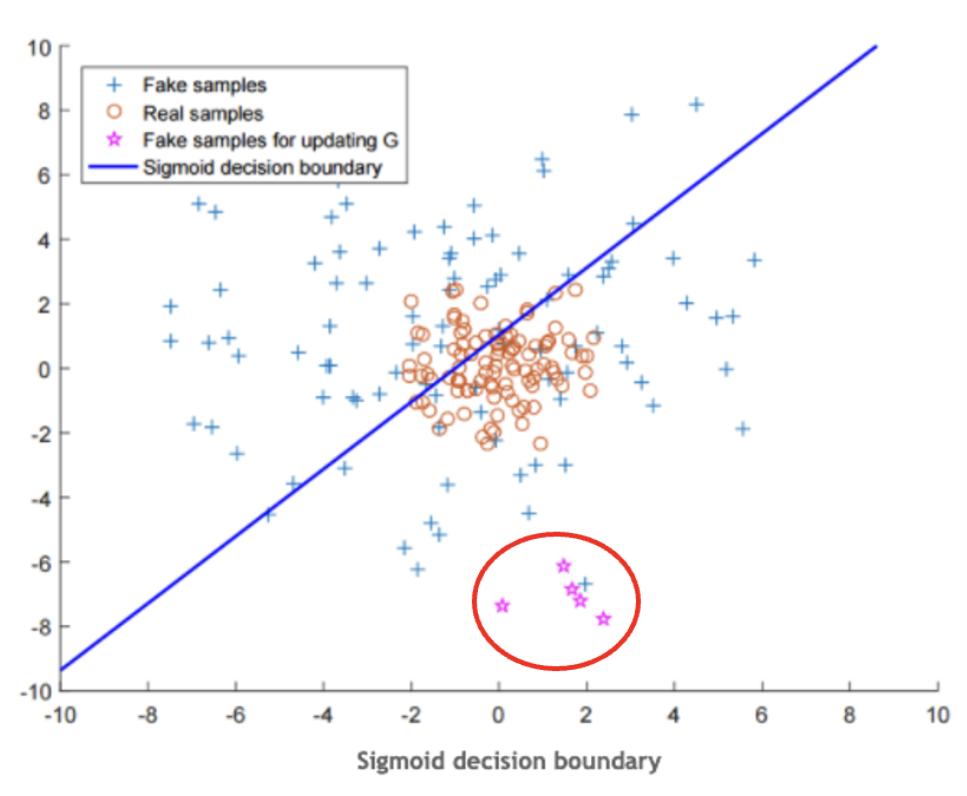
Background
LSGAN의 이론은 단순하지만 효과적이다. 위 그림에서 결정경계인 파란선을 기준으로 아래는 Real로 위는 Fake로 분류한다. 별모양의 데이터의 경우 Fake sample임에도 불구하고 판별자를 완벽히 속여 결정경계로부터 멀리 떨어져있는데 GAN에서는 vanishing gradient 문제로 인해 저 데이터들에 대해 더 학습할 의지가 없다. 이러한 문제점을 보완하고자 별모양의 데이터를 결정경계쪽으로 끌어올려보자는 것이 LSGAN의 아이디어이다.
Loss function

GAN의 vanishing gradient 문제는 Sigmoid cross entropy loss로 인한 것이기 때문에 LSGAN에서는 손실함수로 least square loss를 사용한다. 즉, 결정경계로부터 멀리 떨어진 샘플들에게 페널티를 부여하여 문제점을 해소하였다.
CatGAN
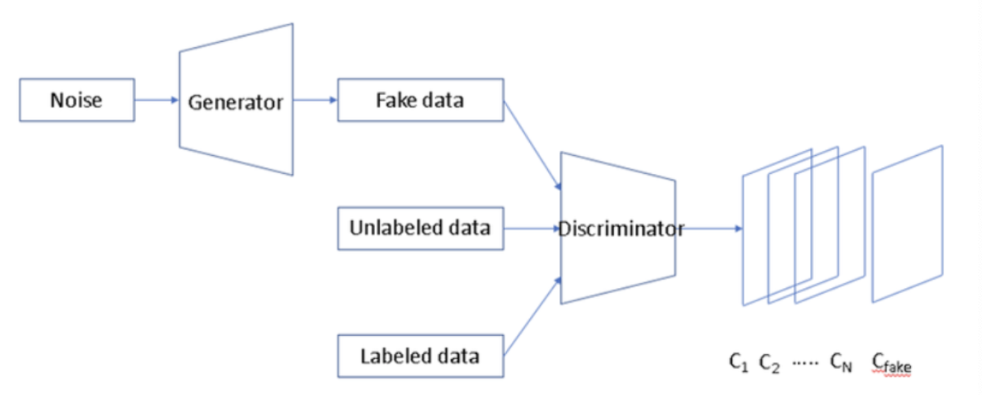
Features
- Semi-supervised learning
- 여러 개의 카테고리로 분류
Object function
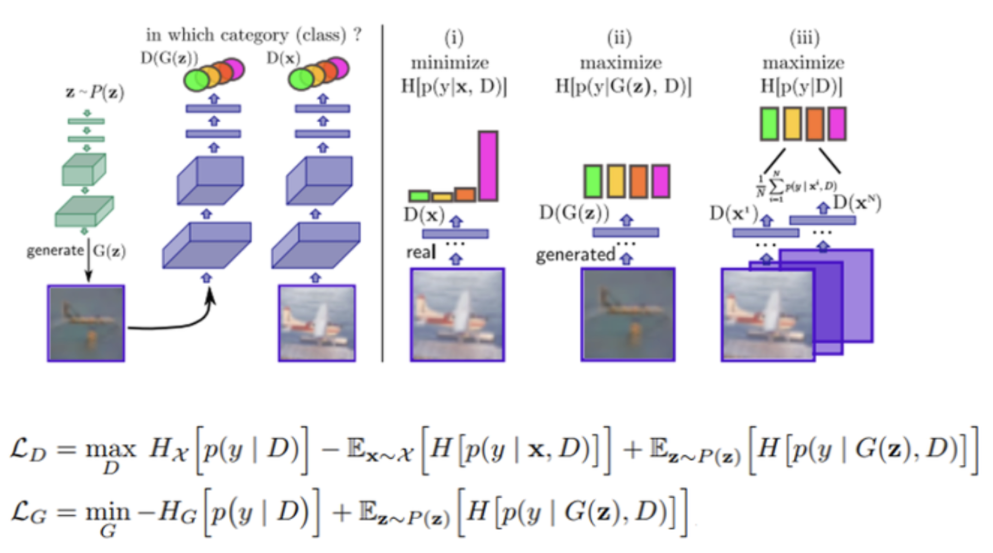
Discriminator
- Real data는 특정 클래스에 속하여야 하므로 엔트로피를 최소화한다.
- Fake data는 class label별로 확률이 비슷하므로 엔트로피를 최대화한다.
- 학습 sample이 특정 class에 속할 확률이 비슷하다 가정하므로 input data에 대한 주변확률분포의 엔트로피는 최대가 되어야 한다.
Generator
- D를 속이기 위해 특정 클래스에 속한 것처럼 보여야 하므로 엔트로피를 최소화한다.
- 생성된 sample은 특정 class에 속할 확률이 비슷해야 하므로 주변확률분포의 엔트로피가 최대화 되어야 한다.
