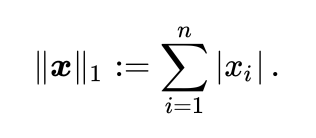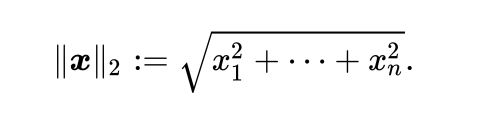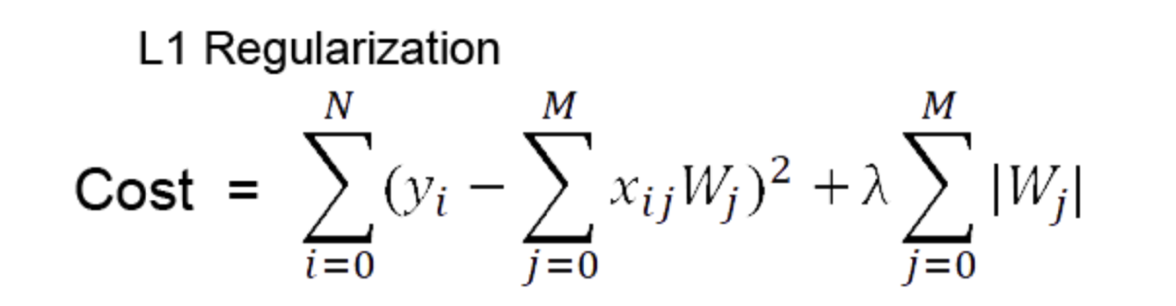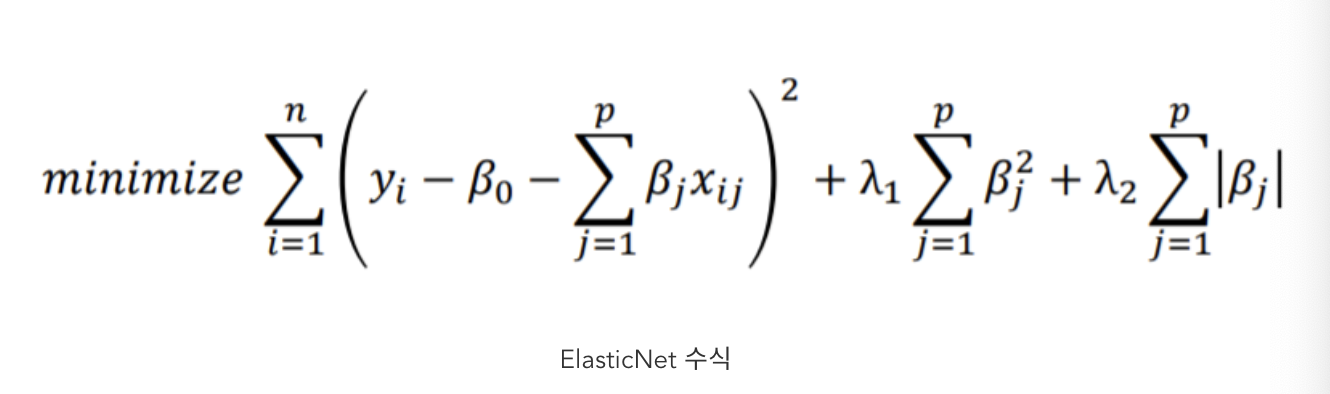[AI] 정규화(Regularization & Normalization)와 표준화(Standardization)

인공지능을 학습시키기 위해서는 기본적으로 많은 양의 데이터를 필요로 하고 처리한다. 그리고 그 데이터 속에서 target 변수와 관련 있는 특성(feature)을 뽑아낸다.

하지만 각 특성(feature)들이 갖는 값의 크기와 단위가 다르기 때문에 직접적으로 비교할 수 없다. 따라서 각 특성들의 단위를 무시하고 값으로 단순 비교할 수 있게 만들어 주어야 한다.

정규화와 표준화를 특성 스케일링(feature scaling) 또는 데이터 스케일링(data scaling) 이라고 한다.

게다가 데이터 값의 범위가 너무 크면 노이즈 데이터가 생성되거나 overfitting이 될 가능성이 높아진다.

정규화(Normalization)

• 값의 범위(scale)을 0~1 사이의 값으로 바꿔주는 것

표준화(Standardization)

• 값의 범위(scale)을 평균 0, 분산 1이 되도록 바꿔주는 것.

정규화 Regularization

모델에 제약을 걸어 overfitting을 줄이는 기법.

• perfect fit을 포기하고, training accuracy를 낮춤으로써 potential fit을 증가시키고자 (testing accuracy를 높이고자) 하는 것.
• 너무 높은 복잡도(complexity)를 피하기 위해서 쓰는 방법
• 대표적으로 drop out, early stopping, weight decay, L1 regularization, L2 regularization등이 있다.

드롭아웃 Drop out

모델의 layer에서 0~1 사이의 확률로 뉴런을 제거(drop) 하는 기법이다.

특정 feature가 타겟 변수에 가장 큰 상관관계가 있다고 가정했을 때, drop-out을 적용하지 않고 모델을 학습하면 해당 Feature에 가중치가 가장 크게 설정되어 나머지 Feature에 대해서는 제대로 학습되지 않을 것이다.

반면 Drop-out을 적용하여 상관관계가 강한 feature를 제외하고 학습해도 좋은 출력값을 얻을 수 있도록 최적화되었다면, 과적합을 방지하고, 나머지 feature까지 종합적으로 확인할 수 있게 된다.

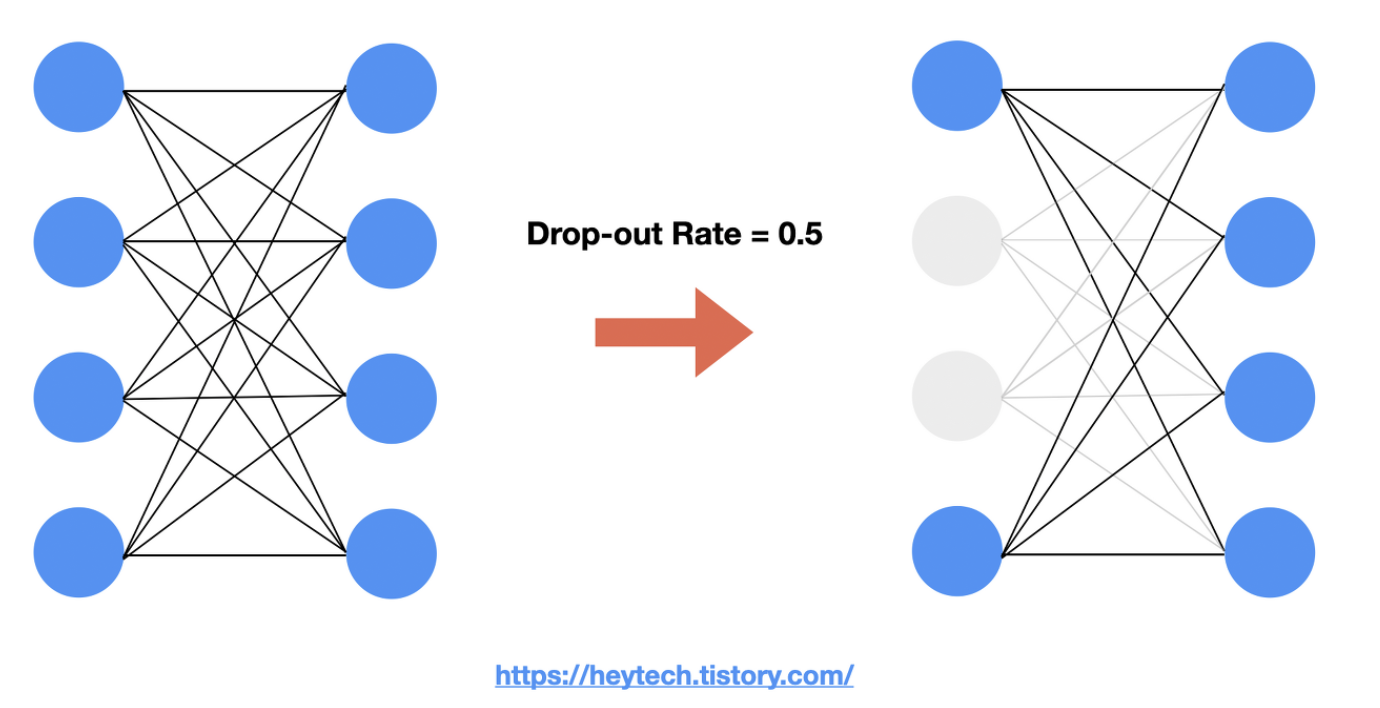
[출처][https://heytech.tistory.com/127]

조기 종료 early stopping

손실 값이 크게 줄지 않을 때 원래 지정했던 iteration 전에 학습을 끝낼 수 있다.

가중치 감쇠 weight decay

학습된 모델의 복잡도를 줄이기 위해서 학습 중 weight가 너무 큰 값을 가지지 않도록 손실 함수에 페널티를 준다. 이 페널티 항으로 많이 쓰이는 것이 L1과 L2 정규화다.

[출처] https://light-tree.tistory.com/216

L1 Regularization과 L2 Regularization

Norm

Norm은 벡터의 크기를 측정하는 방법이다.

L1 Norm

L1 Norm은 맨해튼 거리라고 부르기도 한다. 이 때 L1 Norm은 벡터의 크기를 구하기 위해 벡터의 모든 성분의 절대값을 더한다.

L1 Loss는 실제 값과 예측값 오차의 절대값을 구해 모든 값들을 더한 값이다.

이를 Least absolute deviations(LAD), Least absolute Errors(LAE), Least absolute value(LAV), Least absolute residual(LAR), Sum of absolute deviations 라고 부른다.
출처: https://light-tree.tistory.com/125

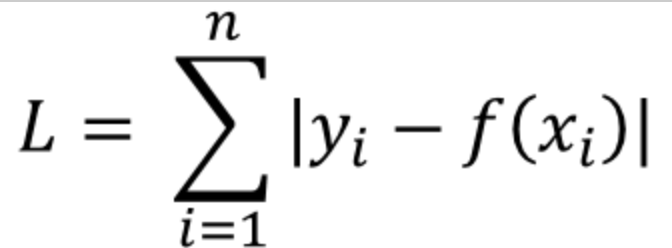
L2 Norm

L2 Norm은 유클리디안 거리라고 부르기도 한다. 이 때 L2 Norm은 벡터의 크기를 구하기 위해 벡터의 모든 성분을 제곱한 값을 더해 루트를 씌운다. 직선거리라고 보면 된다.

L2 Loss는 실제 값과 예측값 오차의 제곱의 합으로 정의할 수 있다.
이를 Least Squares Error(LSE)라고 부른다.

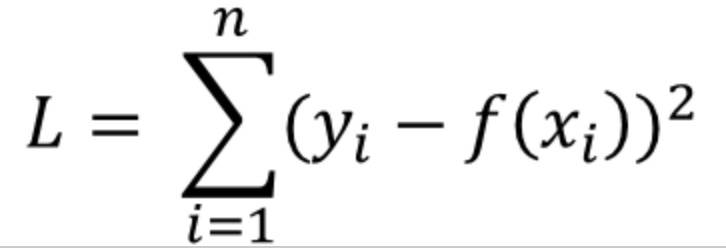
L1 Loss와 L2 Loss 차이

• L2 Loss는 L1 Loss에 비해 outlier에 더 큰 영향을 받는다.
• L1 Loss가 L2 Loss에 비해 outlier에 더 Robust하다.(=강하다 =민감하지 않다)
• L1 Loss는 0인 지점에서 미분이 불가능하다는 단점을 가지고 있다.

L1 Regularization (Lasso 라쏘)

cost funciton에 가중치의 절댓값만큼의 패널티를 붙여 cost가 더 커지게 만들어 overfitting을 방지한다.

따라서 특정 weight들을 0으로 만들 수 있어 원하는 weight만 남길 수 있는 feature selection 역할을 할 수 있습니다. → 즉, 특정 가중치를 삭제해 모델의 복잡도를 낮출 수 있습니다.

람다값이 작을 수록 약한 정규화가 적용된다.

이상치에 강하다. (Robust)

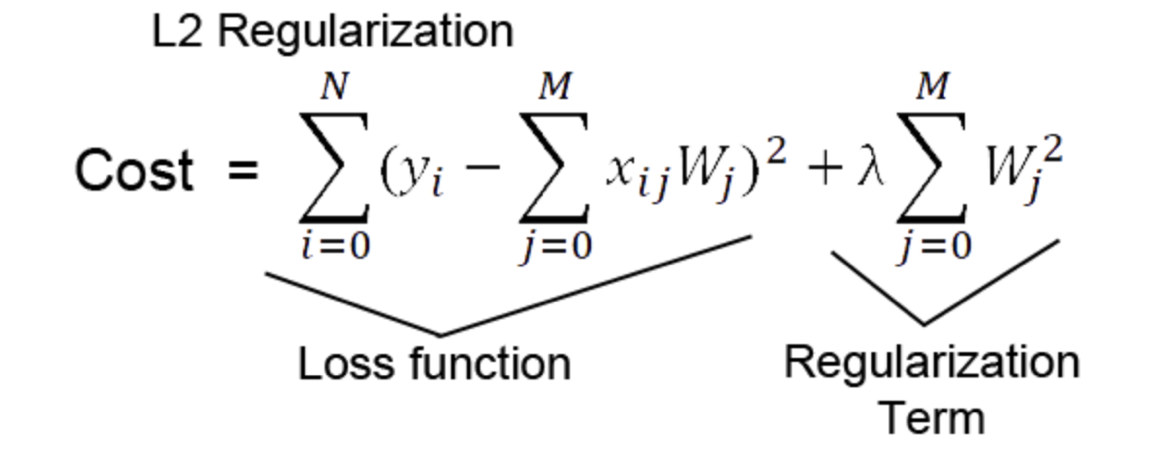
L2 Regularization (Ridge 릿지)

cost function에 가중치 제곱의 합을 더하는 형태로, 가중치의 크기에 따라 가중치의 패널티 정도가 달라지기 때문에 학습 효과가 L1 Regularization 대비 더 좋게 나타난다.

람다값이 작을 수록 약한 정규화가 적용된다.

이상치에 민감하다.

->
이상치가 없고 값이 균등하게 작을 때에는 L2 Regularization의 결과 값이 더 작아지게 되므로 일반적으로 L1보다 L2가 더 좋은 성능을 낸다.

왜냐하면 L1, L2 연산 값을 Error에 더하는데, 이 값이 너무 커져버리면 학습하는 데 방해가 될 수 있기 때문이다.

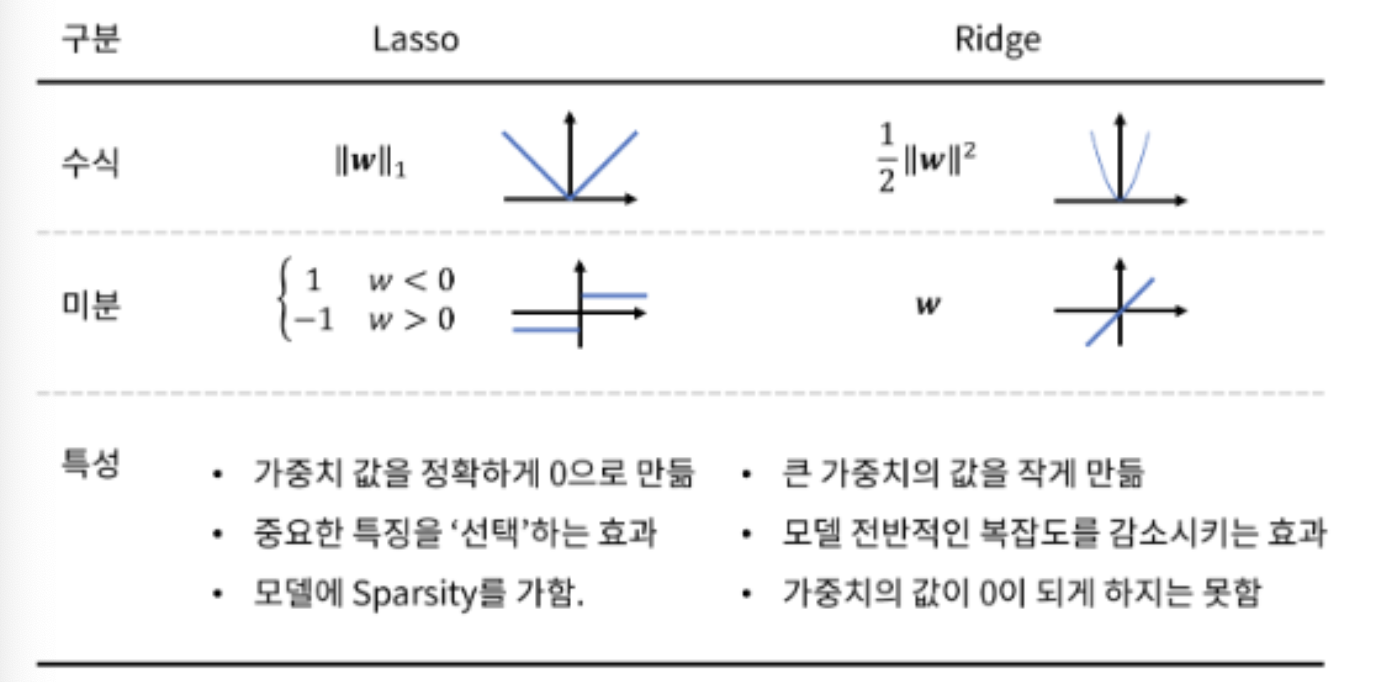
[출처] https://light-tree.tistory.com/125

Elastic-Net

Elastic-Net은 L1 Regularization과 L2 Regularization을 조합해 사용하는 것이다.

lambda_1, lambda_2는 각각 Ridge와 Lasso 속성에 대한 강도를 조절하는 것이다.
이를 통해, Ridge의 정규화 속성과 Lasso의 feature selection 속성을 둘 다 갖는 모델이다.

• Lasso는 상관관계가 있는 다수의 변수들 중 하나를 무작위 선택하여 계수를 축소하는 반면, Elastic-Net은 상관성이 높은 다수의 변수들을 모두 선택하거나 제거한다.
• 이러한 방식을 통해 group effect를 유도한다. 따라서 다수의 변수간에 상관관계가 존재할 때 유용하다.

[출처] https://todayisbetterthanyesterday.tistory.com/12