[CS스터디] 도시를 최단거리로 여행하는 법
0
022) 10개 도시를 최단거리로 여행하는 법
- 알고리즘은 아래와 같은 “시간복잡도(Time Complexity)” 를 갖는다. (몇 가지만 써둔 것임)
- 시간 복잡도란? 컴퓨터 프로그램의 입력값과 연산 수행 시간의 상관관계를 나타내는 척도
- 시간 복잡도의 표기는 점근 표기법을 이용해서 나타낸다. Big-O(또는 Big-Oh) 또는 란다우 표기법(Landau notation) 라고 부르기도 한다.
- O(logN) 이런 식… 으로 O(f(n)로 나타낸다.(아래 내용은 괄호 안에 들어가는 거 적어둔것임)
- 몇가지만 살펴봅시다..
-
log N
ex) 이진검색
-
N
-
NlogN
ex) 퀵 정렬
-
N^2 (2차)
-
N^3 (3차)
-
2^N (지수 복잡도)
-
지수 복잡도(exponential)
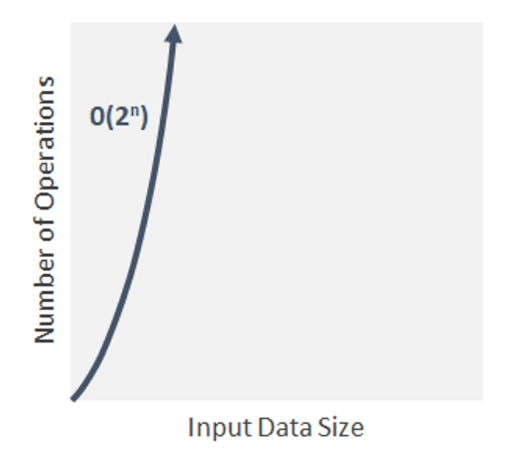
- 2^n의 복잡도로 2^n의 비율로 복잡도가 증가한다.
- 지수 알고리즘 에서는 한 개의 항목을 추가하면 수행해야 할 일의 양이 ‘두 배’가 된다.
- logN과는 정 반대라고 볼 수 있다. (한 개의 항목을 추가하면 수행해야 할 일의 단계는 한 개만 늘어나므로)
- 어떤 상황에서 발생하는가? → 모든 가능한 경우를 하나 씩 시도해 봐야만 하는 상황에서 발생
- 어떤 문제에서 필요한가? → 특히 암호 기법에 사용되는 알고리즘은 특정 계산 과제를 수행하는 일이 지수 복잡도를 갖도록 하는데 기반을 둔다. → 바로 위와 같은 경우 은밀한 알고리즘을 모르면 문제를 바로 푸는 일이 사실상 불가능하다. 바로 이때 필요하다.
- ‘P’(다항 Polynomial)
- 쉬운’ 문제는 복잡도 면에서 ‘다항’ 이다.
- 실행 시간이 ‘다항식’(N^2와 같은 식)으로 표현 되는데. 이러한 부류의 문제를 ‘P’(다항 Polynomial)라고 부른다.
- 즉 이러한 문제(다항 시간 내에 해결할 수 있는 문제)를 P라고 부른다.
- “NP”(Nodeterministic Polynomial)문제
- 다항 알고리즘으로 풀 수 없는 문제를 “NP”문제 라고 한다. → 우리가 아는 다항 알고리즘 으로는 못푼다.
- 빨리 풀 순 없지만 해결책(알고리즘)을 알고 있다면 그것이 맞는지는 빨리(다항 시간 내에) 입증할 수 있다. → 즉, ‘비결정적 다항’ 을 의미한다.
여행하는 외판원 문제(traveling salesman problem)
- 자신이 사는 도시에서 출발해서 다른 도시를 모두 방문하고 나서 다시 출발점으로 돌아와야 한다.(그냥 쉽게 말해서.. 쓰레기 차가 다니는 경로를 최소로 만들어야 되는 것)
- 이 경우! 전체 여행 거리를 최소로 만들기 위해서는 모든 상황을 다 봐야 되므로! NP문제 라고 볼 수 있다.
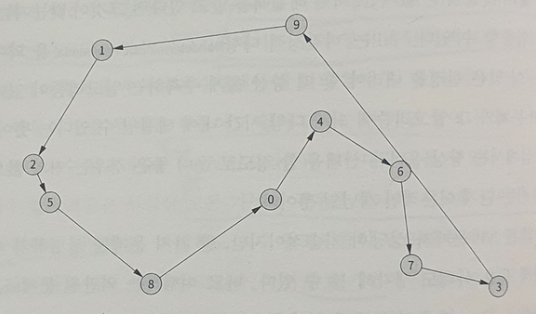
- 그 해법으로는 “‘최근접 이웃’ 휴리스틱”이 있는데. 한 도시에서 시작해서 매번 아직 방문하지 않은 도시 중 가장 가까운 도시로 이동하는 방식.(시작하는 도시가 바뀌면 여행경로 바뀔수있음)
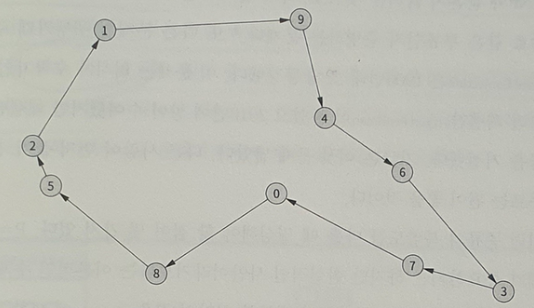
- 하지만 최단 경로를 찾는 방법은 결국.. 모든 가능한 경로를 다~ 시도해보는 방법 뿐…
- 결국 모든~ 경로(18만개)를 다 탐색해서 ! 찾아낸 최단 경로를 보여주는 방법이 나왔다.
즉, 가능한 모든 해법을 완전 탐색 하는 것 보다 더 효율적으로 풀 방법이 없다. 는 말이다.
왜 못푸는가… 그것은 본질적으로 난해하기 때문.. 이라고 의견이 기울고 있음..
이러한 것을 배경으로.. 1971년에 스티븐쿡 이 발표한 연구결과가 있다.
- 이런 문제 중 다수가 서로 동등하다.
- 다항 시간 알고리즘을 찾을 수 있다면 이 모든 문제에 대한 다항시간 알고리즘을 찾아낼 수 있다. 는것이다!
- → 1982년 튜링상 받았다고 한다.
→ 하지만.. 현실에서는 대부분 근사치만 구하는 것으로 충분하기 때문에, 이러한 종류의 복잡도를 다룰 때에는 현실적으로 필요하지 않다. 이론적인 주제 라는 말이다.
반면, 암호 시스템 같은 일부 중요한 응용 분야는 특정 문제는 정말로 풀기 어려울 것이라는 믿음에 기반하므로 이러한 문제에는 필요할 것이다.
