[백준] 11726번 2xn 타일링 - Java, 자바

난이도

실버 3

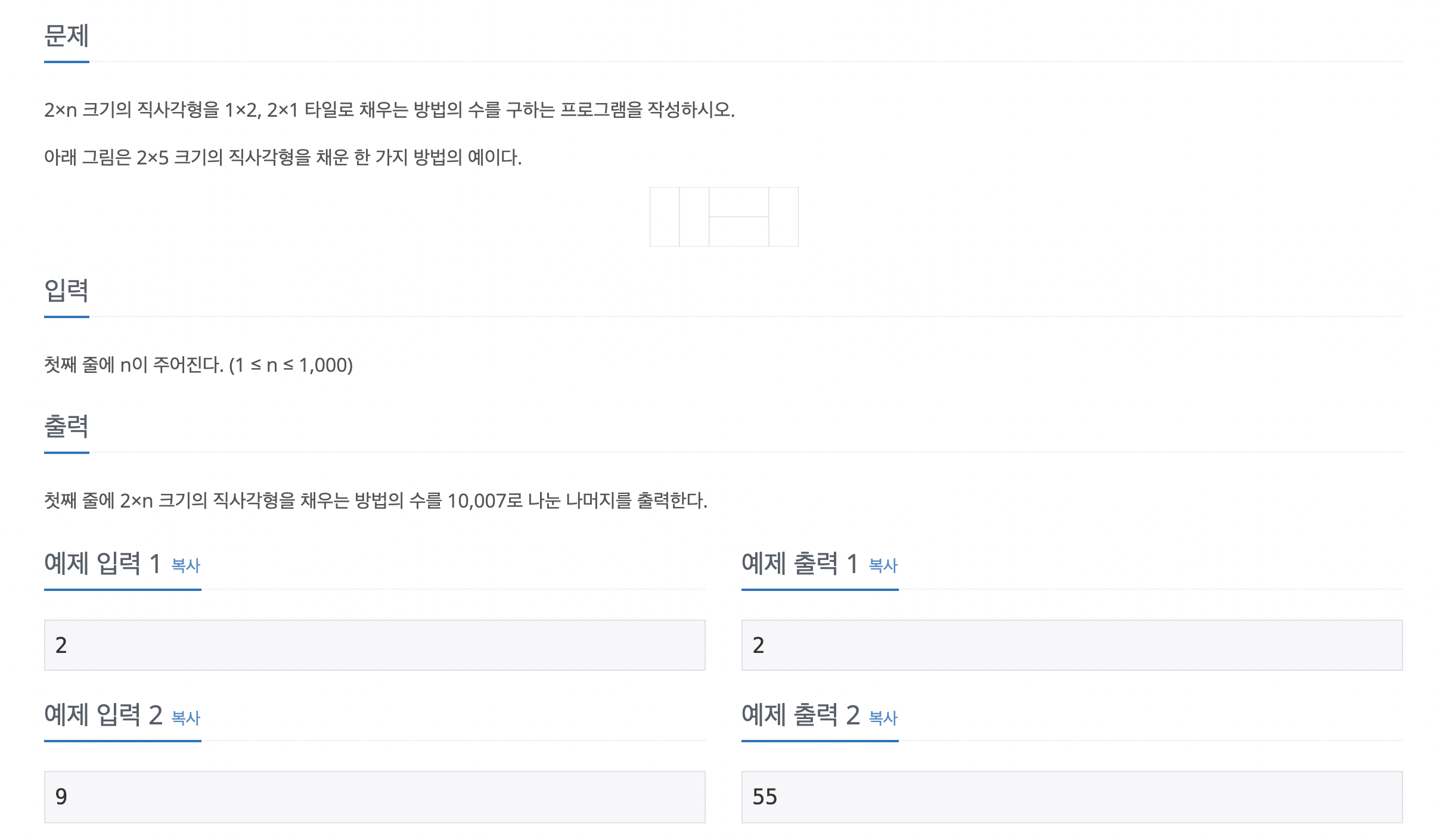
문제

https://www.acmicpc.net/problem/11726

풀이

DP 문제푸는 방법
1. 테이블 정의
2. 점화식 찾기
3. 초기값 정하기

문제에 적용해보자!

1. 테이블 정의

D[i] = 2xi 크기의 직사각형을 1x2, 2x1 타일로 채우는 방법의 수

2. 점화식 찾기

직사각형 맨 왼쪽 위를 채울 수 있는 방법은 위처럼 두가지 방법이 있다.

따라서 점화식은 D[i] = D[i-1] + D[i-2]

3. 초기값 정하기
D[1] = 1
D[2] = 2

위의 과정을 모두 완료했다면 코드를 작성하면 된다.

여기서 한가지 고려할 점이 있다. 백준 문제에서 10007로 나눈 나머지를 출력하라고 명시되어있다. 그래서 마지막 출력시에만 나머지를 적용했다. 하지만 결과는 '틀렸습니다.' ```java System.out.println(dp[n] % 10007); ```

정답은 d[i]을 구할때마다 %10007연산을 해주어야 오버플로우가 나지 않는다.

 for (int i = 3; i <= n; i++) {
            dp[i] = (dp[i - 1] + dp[i - 2]) % 10007;
 }

마지막에만 %10007 연산을 해줄 시 중간에 저장되는 값들이 int값을 넘어서므로 오버플로우가 발생하기 때문이다.

이 점을 고려하여 코드를 아래와 같이 작성하였다.

코드

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;

public class Main {
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        int n = Integer.parseInt(br.readLine());

        int[] dp = new int[1001]; // new int[n+1] 로 하면  런타임 에러(ArrayIndexOutOfBounds) 발생 new int[1001]로 바꿔줌 
        dp[1] = 1;
        dp[2] = 2;
        for (int i = 3; i <= n; i++) {
            dp[i] = (dp[i - 1] + dp[i - 2]) % 10007;
        }
        System.out.println(dp[n]);
    }
}