[백준] 1463번 1로 만들기 - Java, 자바

난이도

실버 3

분류

DP

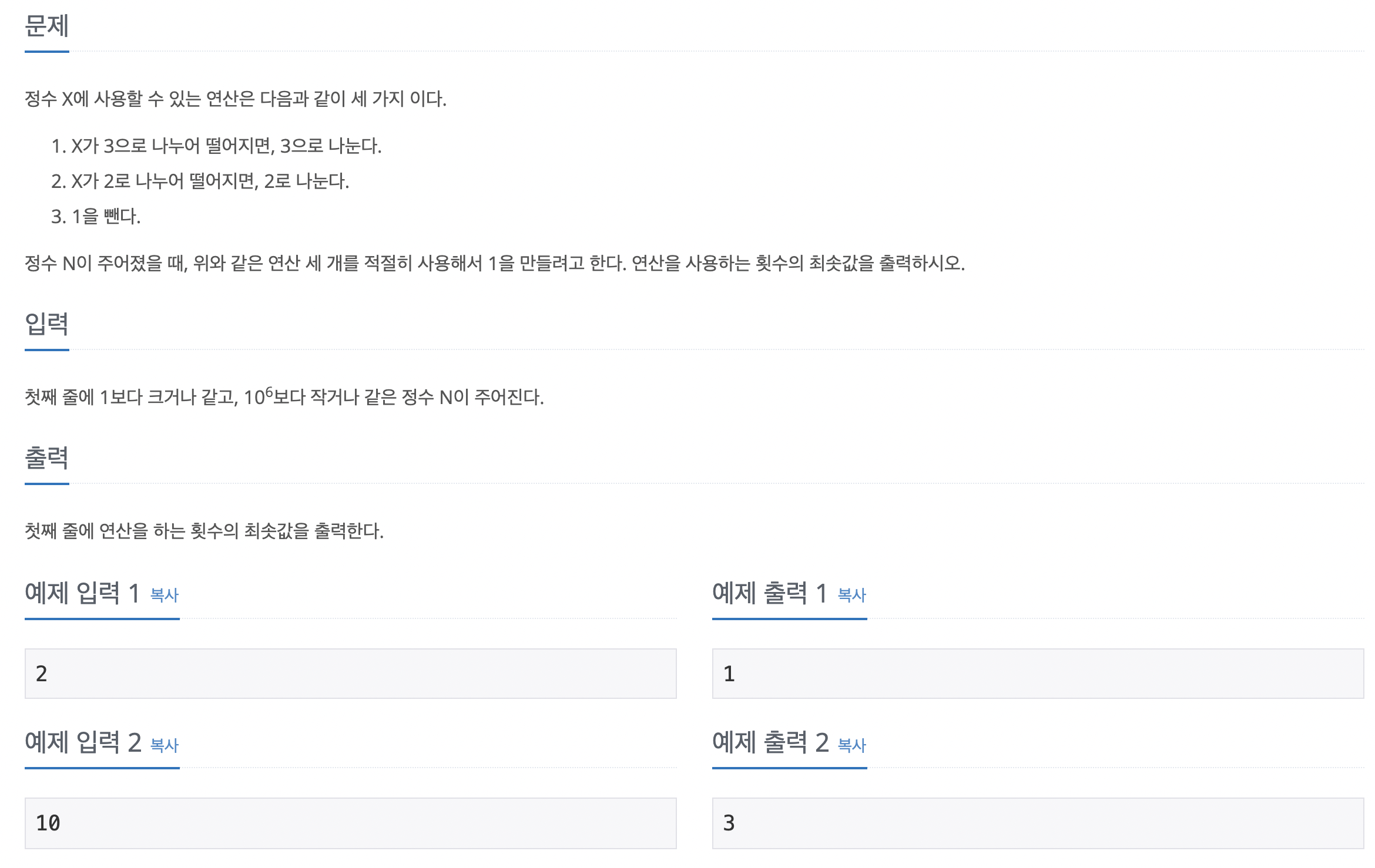
문제

https://www.acmicpc.net/problem/1463

풀이

DP 문제를 풀 땐 3가지 단계를 생각한다.
1. 테이블 정의
2. 점화식 찾기
3. 초기값 정하기

문제에 적용해보자.

1. 테이블 정의

D[i] = 정수가 i를 1로 만들때 연산을 하는 횟수의 최솟값

2. 점화식 찾기

D[12] = ?
3으로 나누거나 (D[12] = D[4] + 1) = (D[k] = D[k/3] + 1)
2로 나누거나 (D[12] = D[6] + 1) = (D[k] = D[k/2] + 1)
1을 빼거나 (D[12]=D[11]+1) = (D[k] = D[k-1] + 1)
-> D[12] = min(D[4] + 1, D[6] + 1, D[11] + 1)
-> D[k] = min(D[k/3] + 1, D[k/2] + 1, D[k-1] + 1)

즉,
-> D[i] = min(3으로 나눌 때, 2로 나눌 때, 1을 뺄 때)

3. 초기값 정의하기

D[0] = D[1] = 0

코드

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;

// 1463번 1로 만들기
public class boj_1_1463 {
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));

        int x = Integer.parseInt(br.readLine());

        int dp[] = new int[x + 1];

        dp[0] = dp[1] = 0;

        for (int i = 2; i <= x; i++) {
            dp[i] = dp[i - 1] + 1; // 먼저 1을 빼준다 
            if (i % 2 == 0) dp[i] = Math.min(dp[i], dp[i / 2] + 1); // 1을 뺀 값과 2로 나눈 값 중 최솟값을 dp[i]에 저장한다 
            if (i % 3 == 0) dp[i] = Math.min(dp[i], dp[i / 3] + 1); // 1을 뺀 값과 2로 나눈 값 중 최소값인 dp[i] 와 3으로 나눈 값 중 최솟값을 dp[i]에 저장한다 
        }

        System.out.println(dp[x]);
    }
}