평균을 모를때?
군집 알고리즘에서는 100개씩 무슨 데이터가 들어있는지 사전 정보가 있었다
하지만 이번엔, 무슨 데이터가 들어있는지 평균을 모른다면 어떻게 대처해야할까?
k-means
- 클러스터 중심을 선정
- 가장 가까운 클러스터 중심을 기준으로 클러스터를 구성
- 클러스터의 평균값을 통해 클러스터 중심을 이동
- 클러스터 중심이 이동하지 않을때까지 2~3을 반복
데이터 설정
우선 데이터를 받아오자
import warnings
warnings.filterwarnings(action='ignore')
import numpy as np
fruits = np.load('fruits_300.npy')
fruits_2d = fruits.reshape(-1,100*100)이제 kmeans 클래스를 호출하여 데이터를 학습시켰다
from sklearn.cluster import KMeans
km = KMeans(n_clusters=3, random_state=42)
km.fit(fruits_2d)
print(km.labels_)
'''
[2 2 2 2 2 0 2 2 2 2 2 2 2 2 2 2 2 2 0 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
2 2 2 2 2 0 2 0 2 2 2 2 2 2 2 0 2 2 2 2 2 2 2 2 2 0 0 2 2 2 2 2 2 2 2 0 2
2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 0 2 2 2 2 2 2 2 2 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 1 1]
'''저런식으로 label에는 0,1,2의 값이 들어가있다
print(np.unique(km.labels_,return_counts=True))
# (array([0, 1, 2]), array([111, 98, 91], dtype=int64))또한 개수를 파악해보면,
- 0 : 111개
- 1 : 98개
- 2 : 91개
임을 확인 가능하다
import matplotlib.pyplot as plt
def draw_fruits(arr,ratio=1):
n=len(arr)
rows = int(np.ceil(n/10))
cols=n if rows<2 else 10
fig,axs = plt.subplots(rows, cols, figsize = \
(cols*ratio,rows*ratio), squeeze=False)
for i in range(rows):
for j in range(cols):
if i*10 + j < n:
axs[i, j].imshow(arr[i*10 + j], cmap='gray_r')
axs[i,j].axis('off')
plt.show()이미지 출력
이제 위와 같은 함수를 정의하여, 배열속 이미지들을 출력하도록 하였다
draw_fruits(fruits[km.labels_==0])
draw_fruits(fruits[km.labels_==1]) 
draw_fruits(fruits[km.labels_==2])
파인애플에 몇개의 사과와 바나나가 섞여있긴 하나, 어느정도는 비슷하게 샘플을 구분하였다
평균 및 기타 정보
draw_fruits(km.cluster_centers_.reshape(-1,100,100), ratio=3)
픽셀의 평균값을 출력하면 위와 같은 모양을 띈다
print(km.transform(fruits_2d[100:101]))
# [[3393.8136117 8837.37750892 5267.70439881]]transform 메소드를 통해 샘플-중심의 거리또한 확인 가능하다
1번째(idx=0)에서 거리가 제일 짦을을 알 수 있다
print(km.predict(fruits_2d[100:101])) # [0]
draw_fruits(fruits[100:101])
출력하여 확인해보면 0번, 파인애플을 나타냄을 알 수 있다
print(km.n_iter_) # 4총 4번 클러스터중심을 이동하였음을 확인 가능하다
최적의 k
k 평균을 위해서 우리는 최적의 k개수를 알아야한다
위 경우는 3개의 타겟이 있음을 알았지만, 운영단계에서는 몇개의 타겟이 있는지 예측하는건 불가능한 일이다
이를 위해 우리는 엘보우 방법을 사용 할 수 있다
inertia = []
for k in range(2,7):
km = KMeans(n_clusters=k,random_state=42)
km.fit(fruits_2d)
inertia.append(km.inertia_)
plt.plot(range(2,7),inertia)
plt.xlabel('k')
plt.ylabel('inertia')
plt.show()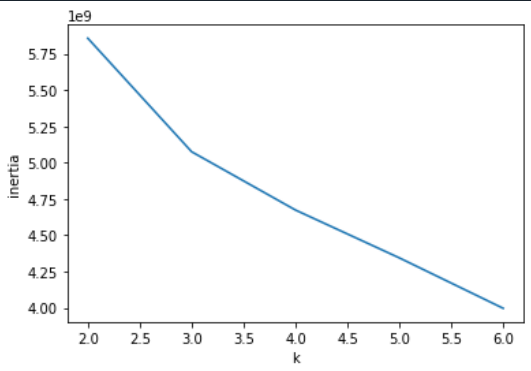
위 그래프에서 세로축은 이너셔(inertia)라고 하며, 샘플들이 얼마나 가깝게 모여있는지를 나타낸다
이때 이너셔가 감소하는 지점이 꺾이는 부분이 최적의 k임을 알 수 있다
이너셔가 줄어드는게 완만해지는 순간, 이너셔를 높히는게 크게 의미가 없어지므로 이너셔를 늘릴 필요가 없어진다

