| 정전기장 | 정자기장 | |
|---|---|---|
| Source | - 근원 점전하 | - 이동 전하 |
| - 점전하: 0차원 | - 전류도선: 1차원 | |
| - 정지한 대전 입자 | - Steady 전류의 형태로 이동 | |
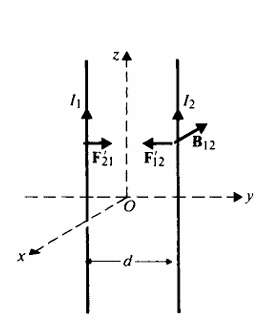
| 방향 | - 방사 방향의 전기장 | - 회전방향의 자기장 |
| 정전기력 | 자기력 | |
| Governing Law | - Coulomb's Law | - Biot-Savart Law |
| 힘의 방향! | - 인력/척력 | - 인력/척력 |
챙의 전자기학 교과서에서는 새로운 벡터장 성분인 자속밀도 와 그에 다른 자기력 를 정의하고 해당 단원을 시작하지만, 자기장에 대한 이해가 잘 되지 않아서 도선에 흐르는 전류에 따른 자기력을 통하여, 자기장의 세기 를 정의하는 방향으로 나아간다.
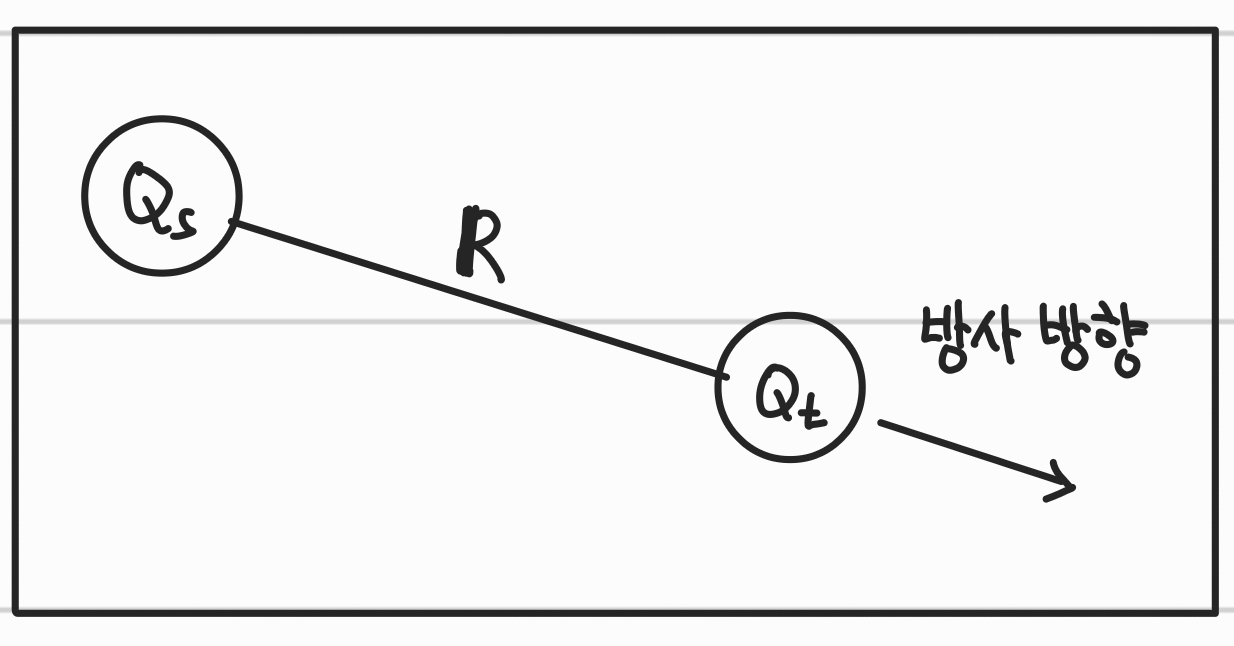
정전기력
- 근원전하와 시험전하
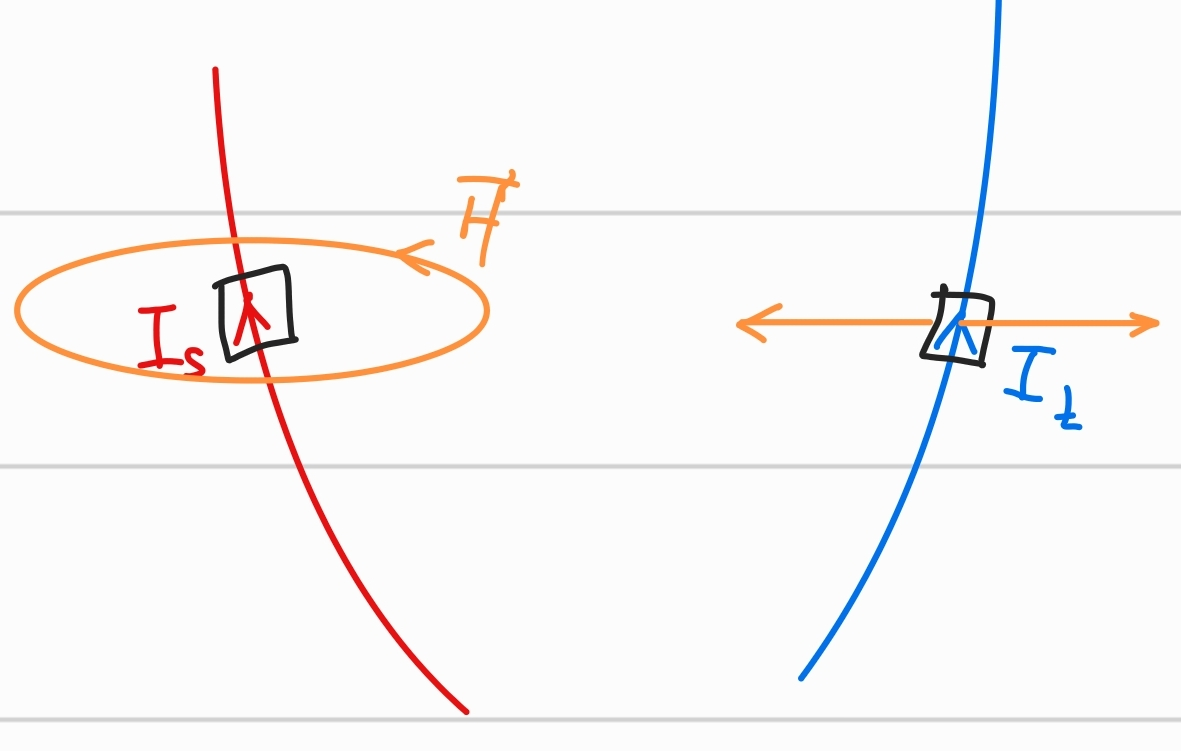
정상 전류에 의한 자기력
- 근원전류도선과 시험전류도선
쿨롱의 법칙과 비슷하게 설명하기 위해
정상전류에 의한 자기장의 생성을 곧바로 설명한다기 보다
물리학자들의 실험결과로부터 얻어진 두 전류가 흐르는 도선을 이용하여 자기력을 먼저 설명하고
자기력으로 부터 합리적으로 보여지도록 자기장의 세기 를 정의한다.
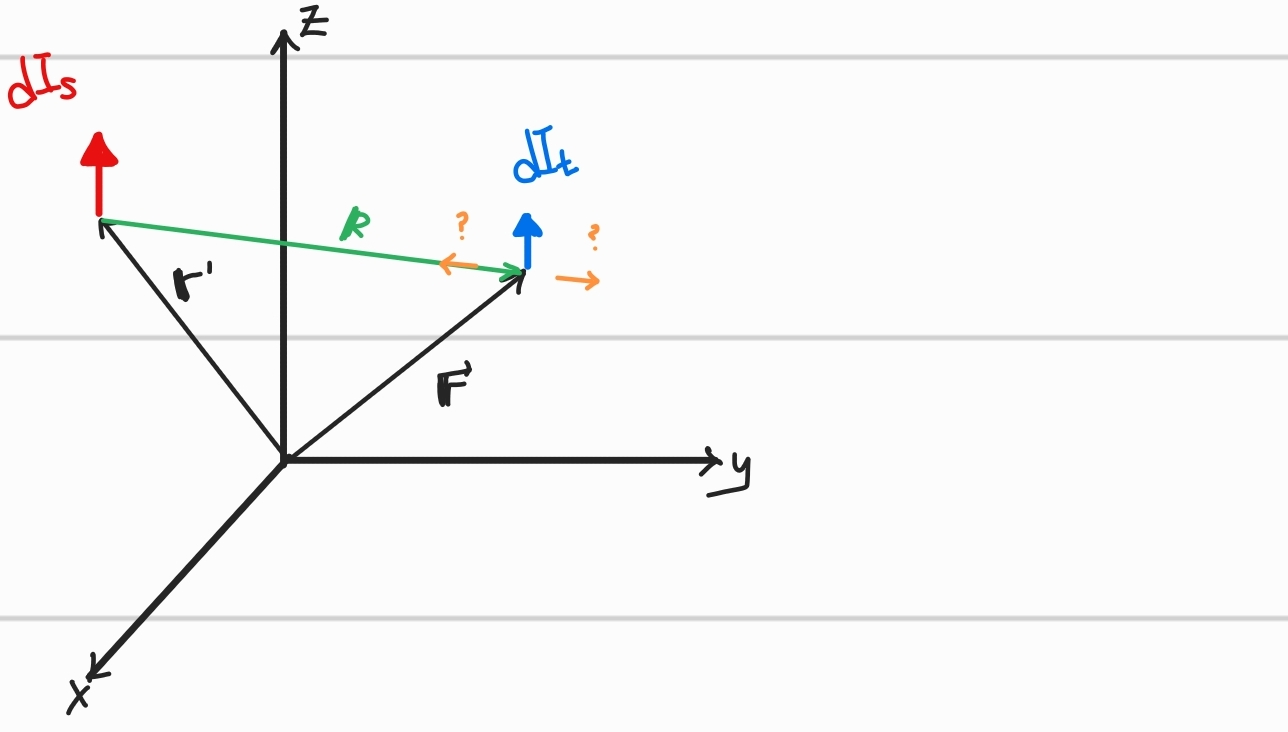
위의 그림과 같이 정상전류가 흐르는 두 도선이 있다.
여러 물리학자 Biot, Savart 등이
두 전류도선(=전류가 흐르는 도선)을 가까이 대면 인력과 척력이 발생한다는 것을 알았다.
전류가 같은 방향이면 인력, 다른 방향이면 척력이였다.
두 전류 도선의 미소부분만 관찰한다고 하자.
두 미소 전류 도선은 전류의 방향에 따라 인력 혹은 척력이 작용한다.
실험결과에 대한 그래프
-
힘에 대해서는
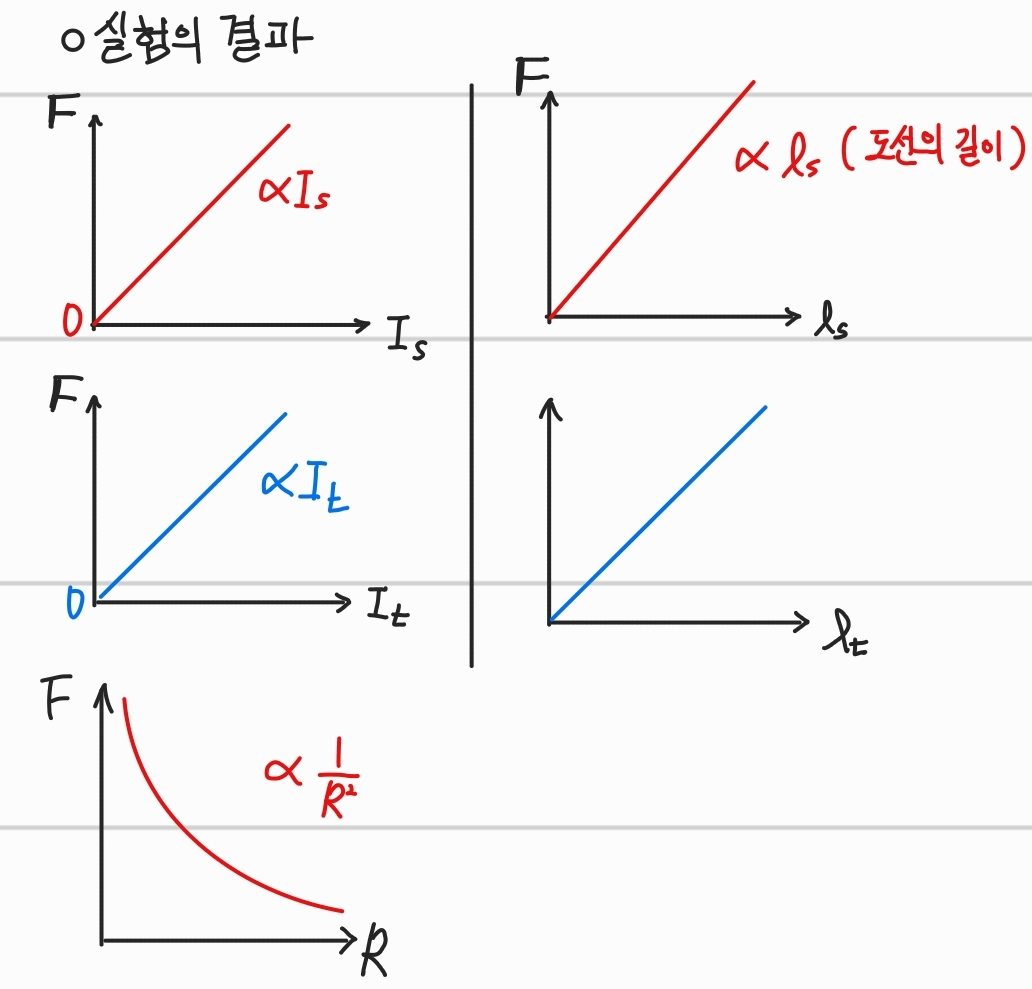
-
방향에 대해서는
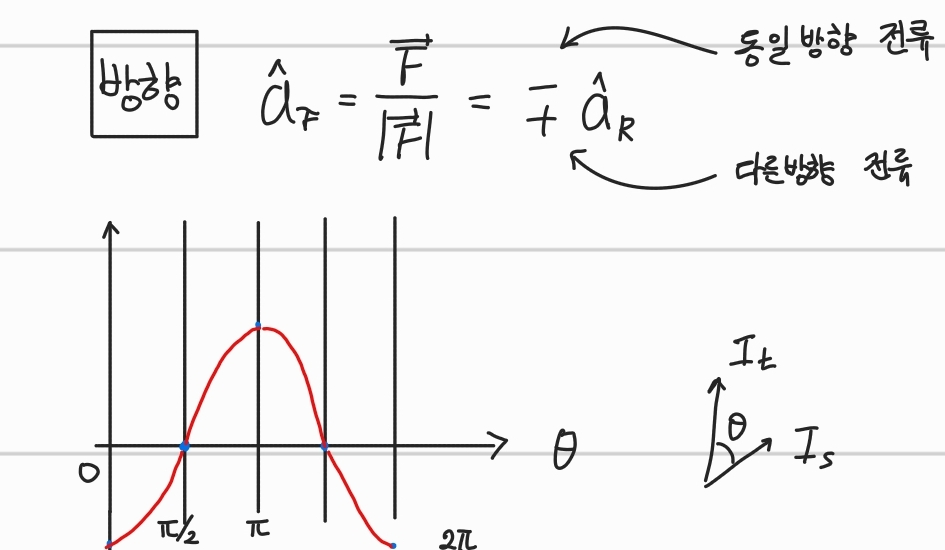
다음과 같이 나왔다는 것이다.
따라서 쿨롱의 법칙과 마찬가지로 위의 결과들을 일반화하여 정리한 수식은 다음과 같다. 실험적으로 결정한 공식
방향을 인력과 반발력으로 맞추기 위해
를 넣었다고 생각하면 된다.
여기서 비례 상수를 더해서 완전한 식으로 만들어주면 다음과 같다.
미소 힘 는 파란색으로 나타나는 시험 전류 도선에 관한 항과 빨간색으로 나타나는 근원 전류 도선에 관한 항으로 나눌 수 있다.
이 다음으로는 미소 자기장의 세기인 를 정의한다.
Coulomb Force로부터 시험전하에 무관하게 전기장을 정의했던 것 처럼
시험 전류도선과 무관하게 어떤 값을 정해줄 수 있을 것이다. 따라서
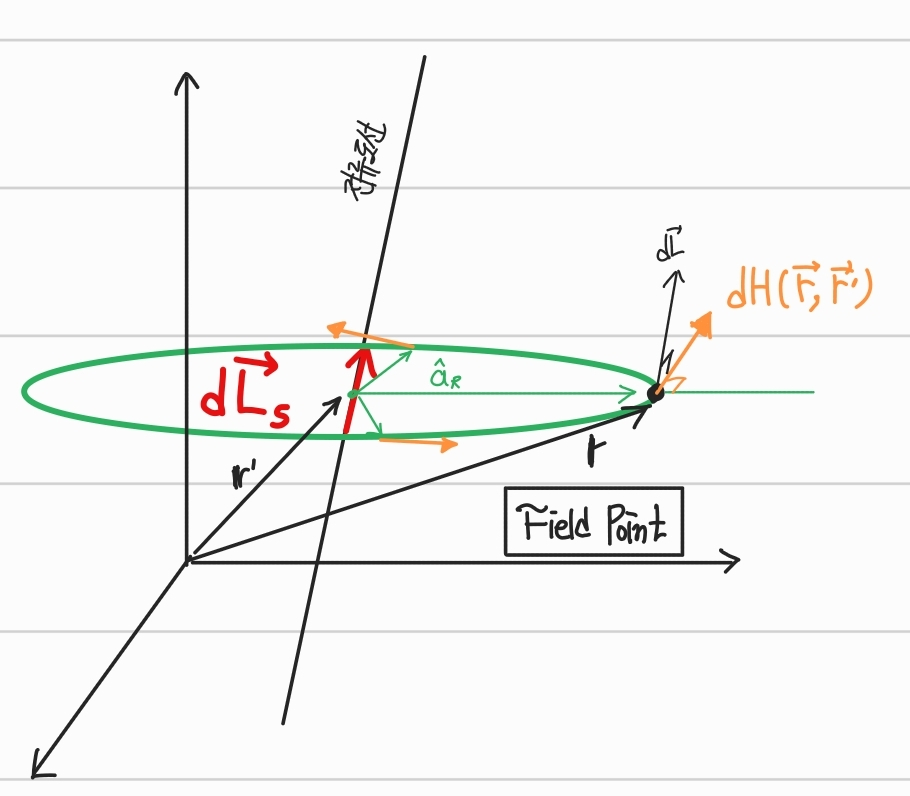
미소 자기장의 세기
여기서 전류도선의 미소 길이 는 Source Point에 해당하므로 이다.
다음과 같이 정의된 자기장의 세기는 회전의 특성을 가지고 있다는 것을 알 수 있다.
또한
자기장의 세기 는
전체 근원전류도선을 Source Point에 대해 적분하면
비오 사바르의 법칙
The integration is along the current path, in the direction of the flow; dl is an
element of length along the wire.