정전기장 3-8 전속밀도와 유전상수

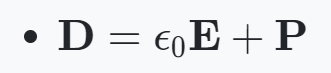
3-8 전속밀도와 유전상수

전속밀도 정의의 이유

• $\mathbf{E}=\frac{1}{4\pi\epsilon}\frac{Q_s}{R^2}\mathbf{a}_R$ 이다.

• $\epsilon=\epsilon_0\epsilon_r$

• 이를 보면 $\epsilon$에 의해 매질에 의한 영향이 있음을 알 수 있다.

• 매질에 따른 영향이 없는 어떤 값을 정의하고 싶었을 것이다.

Gauss's Law 에 따르면


$\nabla\cdot\mathbf{E(\mathbf{r})}=\frac{\rho(\mathbf{r'})}{\epsilon_o}$ 이다.

* 이는 전기장과 전하분포간의 관계를 특정지점(Point Form)으로 설명하는 것이다

유전체가 존재하는 경우

외부 전기장이 가해지고 유전체가 존재하는 경우

• $\rho(\mathbf{r'})=\rho(\mathbf{r'})_f+\rho(\mathbf{r'})_b$

전하밀도는 free charge density와 bound charge density로 구성될 수 있다.

앞서 분극의 개념을 살펴보았을 때, 유전체는 등가체적전하밀도 $\rho_p$로 볼수 있다는 것을 알았다.

처음에 이게 무슨 소리인가 했지만, 금방 알 수 있다.
유전체는 전기적으로 중성이므로 총 전하량이 0이다.
그런데 어떻게 전하밀도를 가진다고 볼 수 있는가..?

분극된 유전체는 등가 분극면전하밀도나 등가 분극체적밀도로 대체될 수 있다

• 전하쌍극자가 가지는 전기장과 전위를 보면 전기쌍극자는 전기적으로 중성 $\rho_{total}=0$ 이지만 마치 전하처럼 보인다는 것이다.
• 그래서 분극된 유전체는 등가 분극면전하밀도나 등가 분극체적밀도로 대체될 수 있다! $\rho_{ps}, \rho_s$

다시
$\nabla\cdot\mathbf{E(\mathbf{r})}=\frac{\rho(\mathbf{r'})}{\epsilon_o}$
이때의 $\rho$의 단위는 단위체적당이므로 유전체를 등가 분극체적밀도로 대체할 수 있을 것이다.

따라서 다음의 식을 만족한다.

$\nabla\cdot\mathbf{E}=\frac{\rho+\rho_{ps}}{\epsilon_o}$

• 정의에 의해 등가 분극체적밀도는 분극벡터의 발산으로 나타낼 수 있다

• $\rho_{ps}=-\nabla\cdot\mathbf{P}$

• $\nabla\cdot(\epsilon_0\mathbf{E}+\mathbf{P})=\rho$

새로운 벡터 D를 정의하며 전속밀도 혹은 전기 변위라고 한다.

• $\mathbf{D}=\epsilon_0\mathbf{E}+\mathbf{P}$

이렇게 정전기장을 설명하는 두 개의 기본 미분식이 나왔고, 모든 매질에 적용 가능하다.

• $\nabla\cdot\mathbf{E}=\frac{\rho}{\epsilon_0}$
• $\nabla\cdot\mathbf{D}=\rho$

적분형으로 나타내면 다음과 같다.

$\oint_s\mathbf{D}\cdot d\mathbf{s}=Q$

임의의 폐곡면을 투과하는 전기적 분극에 의한 총 전속의 방출량은 폐곡면 내부에 있는 총 전하량과 같음을 의미한다.

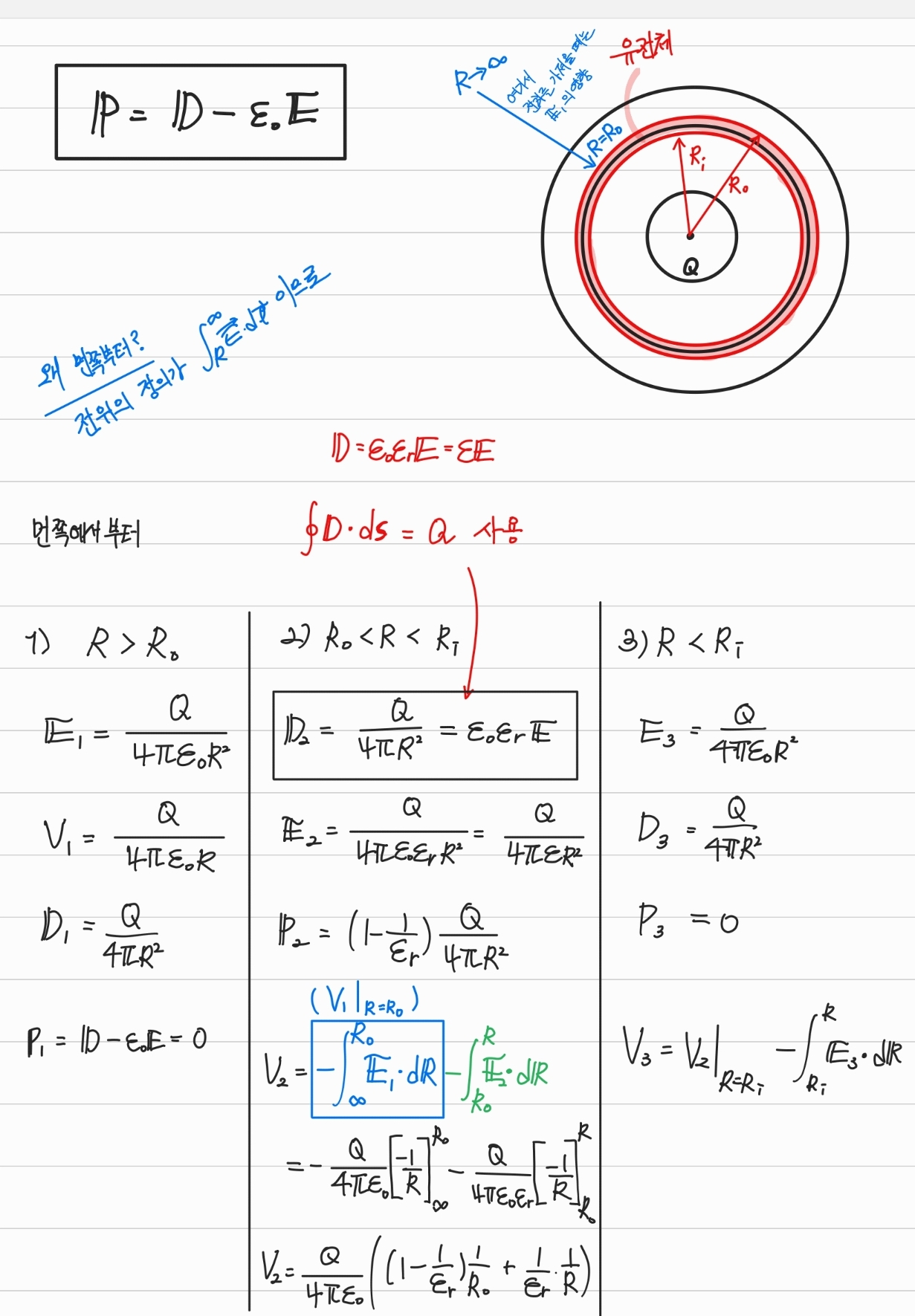
• 예제 3-12를 풀어보고 마무리함.
• 

---

• 
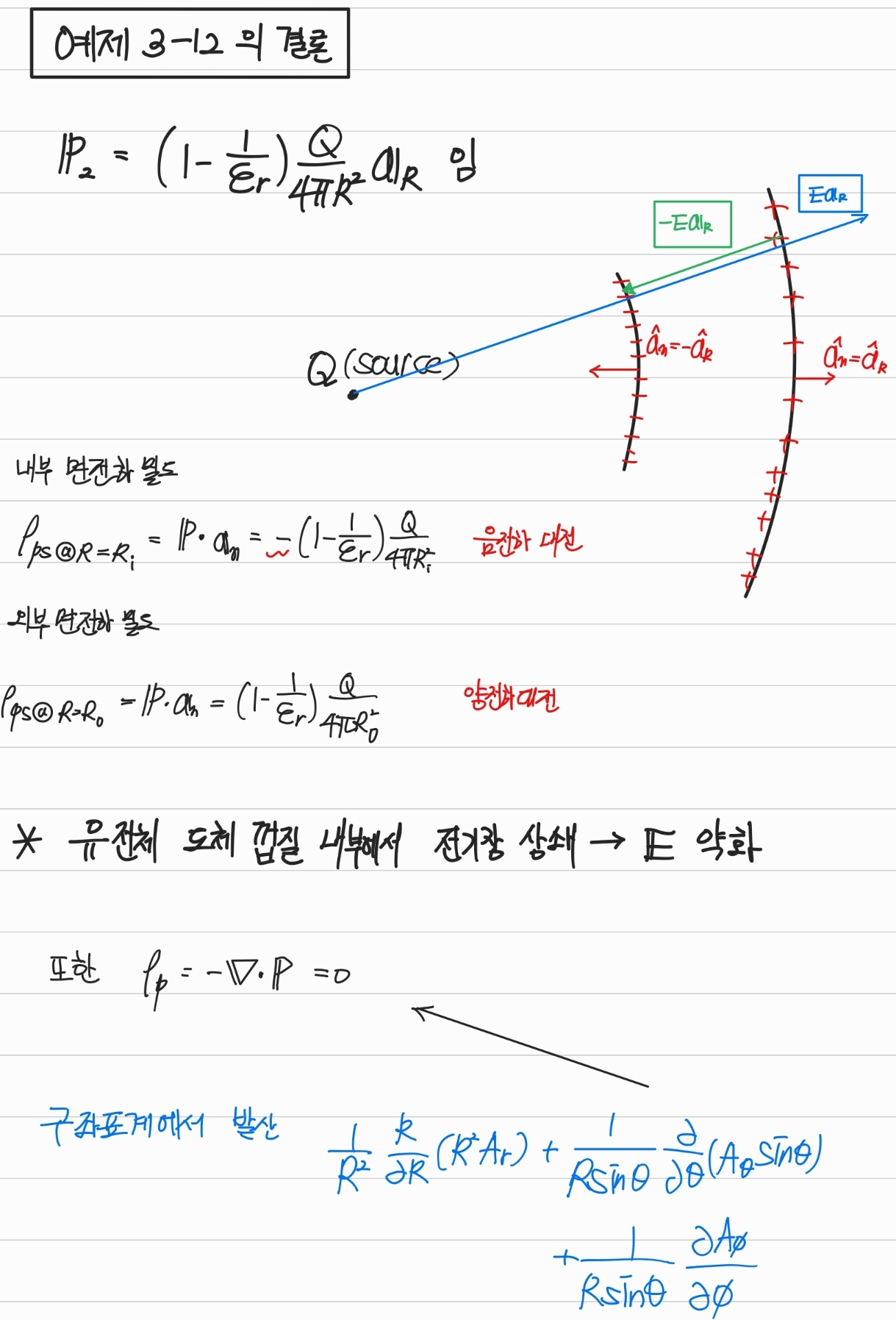
• 위 문제의 풀이를 보면 영역 2에서 $\mathbf{D}$를 먼저 구했음을 알 수 있다.
  이는 매질에 상관이 없기 때문에 구하기 가장 쉽기 때문이다.(이 문제는 $\mathbf{E}$부터 구해도 쉽지만)
• 유전체의 면전하밀도를 계산해보면 안쪽에는 음전하가 바깥쪽은 양전하가 대전됨을 알 수 있다.