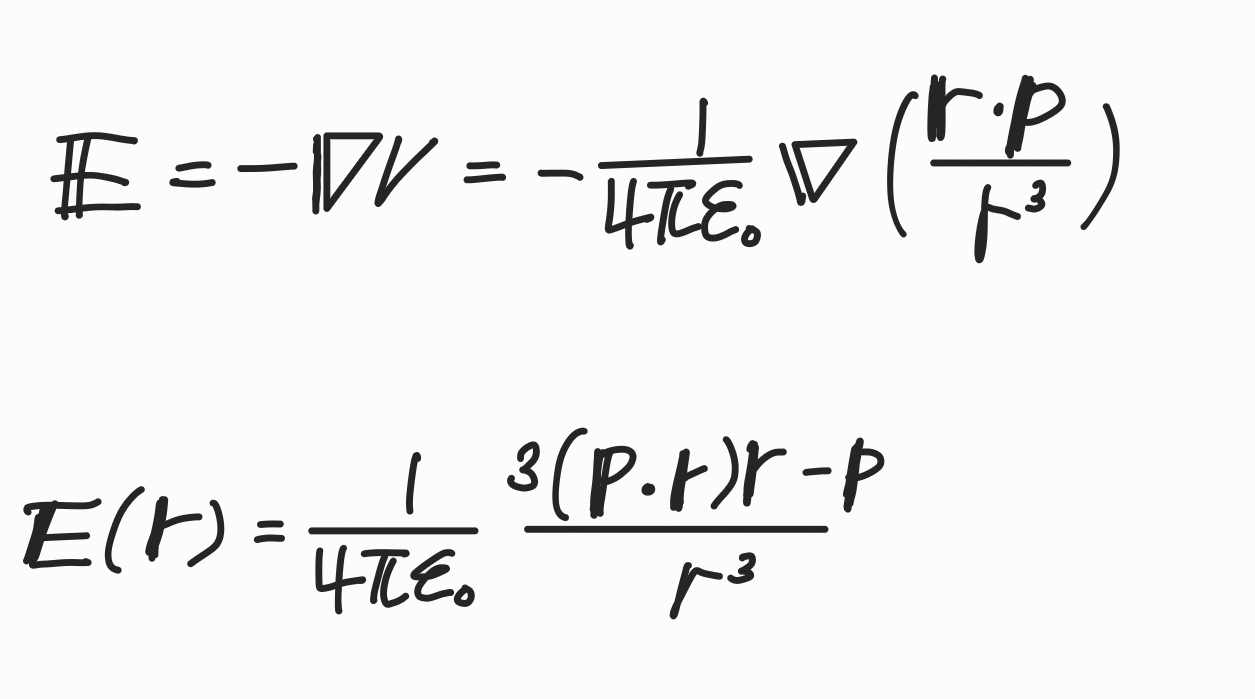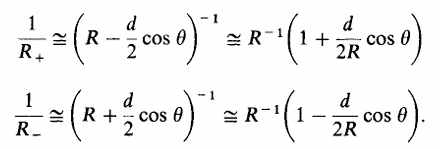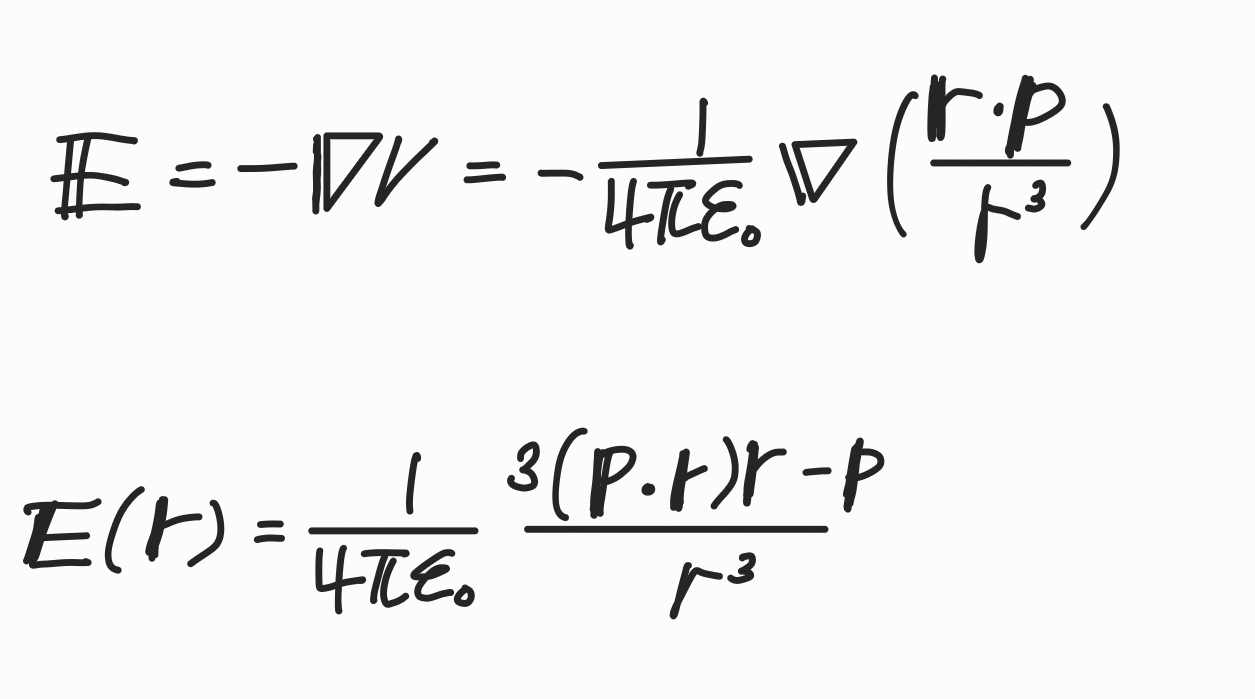정전기장 3-x , Electric Dipole and Multipole expansion scalar potential

전기 쌍극자

서로 다른 두 개의 전하만 존재하는 경우이다.

전기 쌍극자의 개념은 유전체 매질에서 전기장을 이해하는데 중요한 수단이 된다. 따라서 전기 쌍극자에 의한 전기장과 전위 등을 이해하고 넘어간다.

각 전하에 의한 전기장의 세기를 중첩시켜 결과를 얻을 수 있지만, 전위 개념을 사용하여 조금 더 쉽게 전기장 세기를 구해보도록 하겠다.

무한 거리 지점을 기준으로 점전하에 의한 전위 분포로부터
$V=\frac{q}{4\pi\epsilon_0R}$
쌍극자에 의해 발생하는 개별 전위값의 합은 다음과 같다.

전하 분포에 의한 전위

---

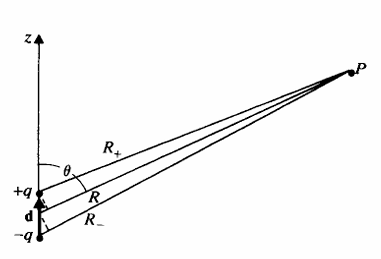
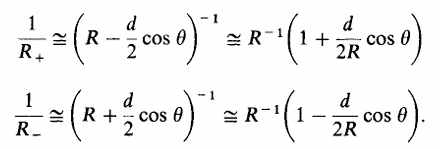
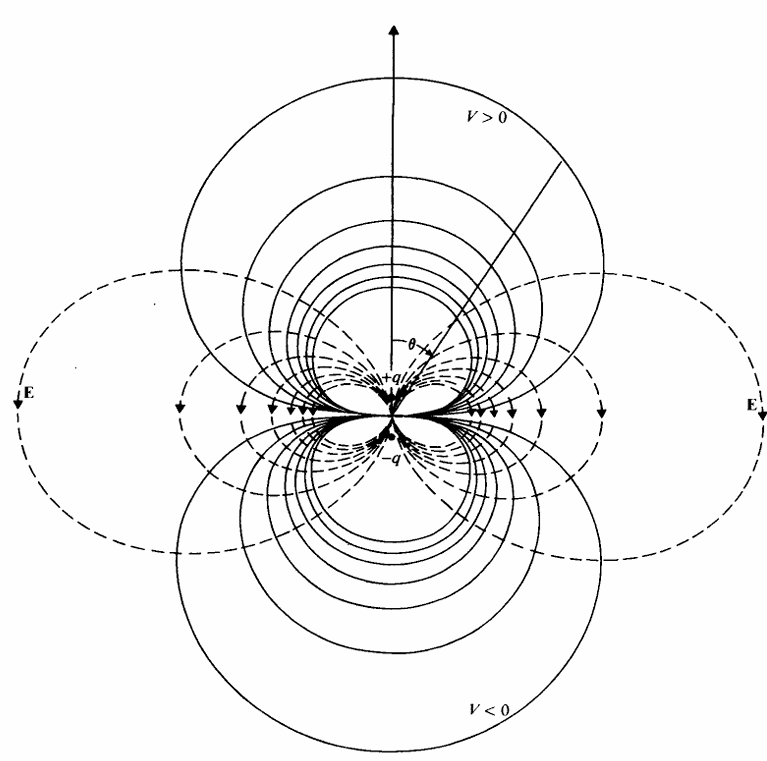
균일한 전기장에 전기쌍극자가 놓이는 경우를 생각해보자.

---

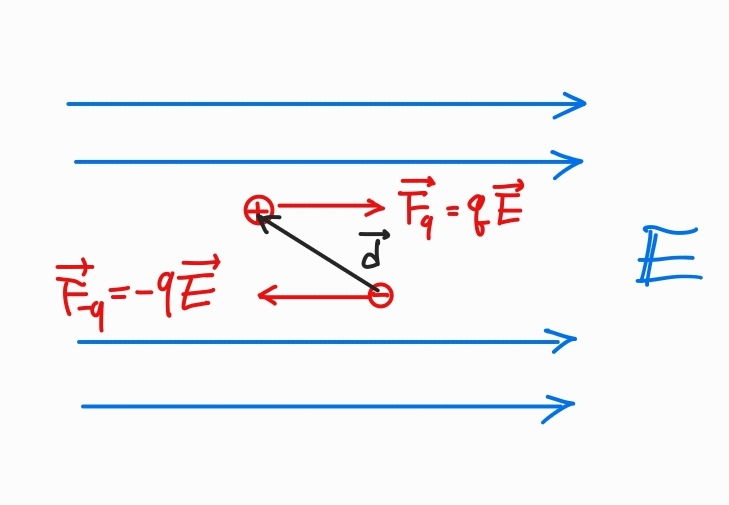
전기장이 전기 쌍극자에 작용하는 전기력 $\mathbf{F}=0$이다.

하지만, 균일한 전기장은 전기 쌍극자에 토크를 작용한다.
$\mathbf{\tau}=q(\mathbf{r}_2-\mathbf{r}_1)\times \mathbf{E}=\mathbf{p} \times \mathbf{E}$

조금 더 일반적인 경우를 살펴보자

Multipole expansion scalar potential

주어진 식은 단일 전하뿐만 아니라 연속적인 전하 분포에 대해서도 적용 가능
이 식을 다양한 방법으로 근사하여 다중극 전개를 얻을 수 있다.
다중극 전개는 멀리 떨어진 관측점에서 전위를 효율적으로 계산하는 데 유용함.

• 조건 1: 전하분포 $\rho(\mathbf{r'})$가 유한한 영역에 분포됨
• 조건 2: 전하분포 $\rho(\mathbf{r'})$로부터 아주 먼 곳의 Potential을 구한다.

---

Taylor Series Expansion

---

대입하면 스칼라 포텐셜은 다음과 같다.

$\mathbf{V}(\mathbf{r})=\frac{1}{4\pi\epsilon_0} \int_Vdv'\rho(\mathbf{r'})(\frac{1}{\mathbf{r}}+\frac{\mathbf{r} \cdot\mathbf{r'}}{r^3}+......)$
$r'$에 대해 적분이다.

$\mathbf{V}(\mathbf{r})=\frac{1}{4\pi\epsilon_0}(\frac{q}{r}+\frac{\mathbf{r} \cdot\mathbf{p}}{r^3}+......)$

여기서 첫 항$\frac{q}{r}$은 단극자 모멘트에 해당함.

$q =\int_Vdv'\rho(\mathbf{r'})$ 이다.

전하 분포가 유한하면, 다 더한 전하분포가 멀리서 보면 점전하처럼 보인다는 것이다.

두번째 항은 쌍극자 모멘트로 정의된다.

$\mathbf{p}=\int_Vdv'\rho(\mathbf{r'})\mathbf{r'}$

전하 밀도에다가 r'을 곱해서 다 더한 것.

$\mathbf{p}=\displaystyle\sum_i q_i\mathbf{r}_i$
이렇게도 나타낼 수 있다.

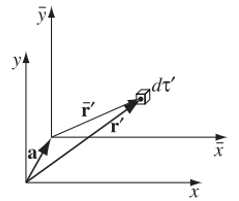
쌍극자 모멘트는 좌표계에 따라 달라지는 값이다.
이는 좌표계와 불변인 것과는 다르다.

쌍극자의 경우 첫 번째 항이 $0$인 경우이다.

첫 번째 항의 전하 q가 +q, -q로 상쇄되면 2차항이 남게 된다.

쌍극자 모멘트가 $\mathbf{p}$일 때 원점에 놓인 전기 쌍극자의 스칼라 퍼텐셜은 다음과 같다.

$\mathbf{V}(\mathbf{r})=\frac{1}{4\pi\epsilon_0}\frac{\mathbf{r}\cdot\mathbf{p}}{r^3}$

이것으로 $\mathbf{E}$를 구할 수 있다.