정전기장 3-x(2) 유전체와 유전상수

유전체(dielectric material)는 Capacitor의 구성요소이고 전자 재료/부품의 구성요소이므로 이해하는 것이 중요하다.

유전체는 전하쌍극자(electric dipole-edp)의 집합체로 구성된 물질이다.

어떤 물질이 전하중성이라면 $\rho(\mathbf{r})=0 [C/m^3]$ 이다.
$\rho(\mathbf{r})=0$ 이면 진공(전하가 없음)일 수도 있지만,
$\rho_{m+}+\rho_{m-}=0$ 으로 양의 전하와 음의 전하의 양이 같을 수도 있다.

유전체는 전하가 켤레로 존재하는 물질이다.

켤레간의 간격 $\mathbf{d}$
전하의 크기 $Q$
전하 쌍극자의 농도
모두 재료에 따라 다르며 중요한 인자이다.

이전 포스트에서 정전기장 내에서 전하쌍극자에 작용하는 힘, 토크, 전위 등에 대해 다뤘다.

전기장 내에서 유전체의 분극을 알아보고 여러가지 중요한 인자들을 정의해본다.

$n_{EDP}$, 상대적 유전율, $\chi_e$, $\mathbf{D}$ 등


전기장 내에서 전하쌍극자 하나가 어떻게 작용하는 지 살펴봤으니, 이번에는 전하쌍극자의 집합체인 유전체가 전기장 내에서 어떤 지 알아본다.

유전체의 특성

• $\mathbf{p}=Q \mathbf{d}$ 유전체를 구성하는 전하쌍극자

• $n_{edp}=\frac{N_{edp}}{\Delta V} [1/m^3]$ 농도

• $\epsilon$ (상대적 유전율) 전기장이 가해짐 -> 분극 -> 유전체의 전계강도 -> 상대적 유전율!

유전체의 전기적 특성

균질한 이상적 유전체를 살펴본다. 전기전도성 $\sigma=0$인 무손실 유전체이다.
$\sigma=0$ 은 이동 가능한 양전하 음전하가 모두 없다는 것이다.

• 전기장이 인가되기 전
• 분극
• 분극 후

1) 전기장이 인가되기 전

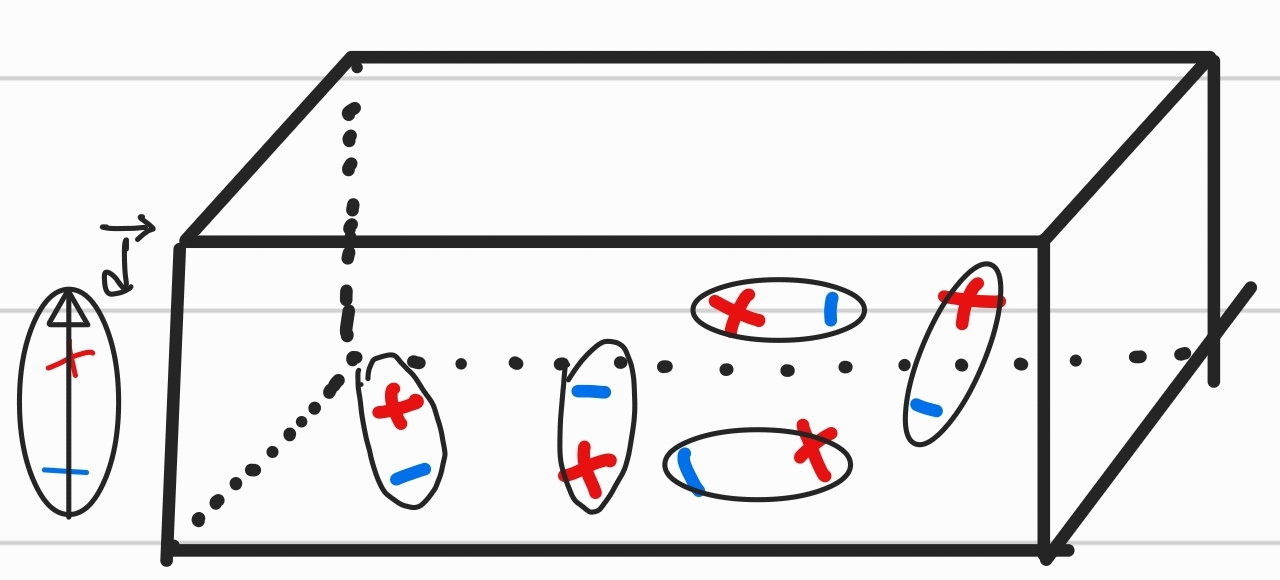
전기장이 인가되기 전에는 전하쌍극자들은 불규칙 배열(Random Orientation)을 하고 있다.
각 전하쌍극자에 대해,
$\mathbf{p_i}=Q\mathbf{d}=Qd\mathbf{a} _d$ [C/m]
Random Orientation을 하고 있으므로 평균적으로 $\mathbf{p}=0$일 것이다.
$\displaystyle\sum_{i=1}^{N.edp}\mathbf{p_i}=\mathbf{p_1}+\mathbf{p_2}+\cdots+\mathbf{p_{N.edp}}=0$
단위 체적당으로 평균을 낸 것을 대문자로 정의한다.
$\mathbf{P}\triangleq \frac{\displaystyle\sum_{i=1}^{N.edp}\mathbf{p_i}}{\Delta V} [C/m^2]$
여기서 주목해야할 점은 등가 전하 밀도인 $\mathbf{D}$와 같은 단위를 가진다는 것이다.

또한 $\mathbf{E}=0$ 인 경우 $\mathbf{P}=0$ 이다.

2) 전기장이 인가됨 $\mathbf{E}\neq0$

$\mathbf{T} \neq0$이므로 전하 쌍극자들이 회전력을 가지며 전기장의 방향으로 정렬된다.

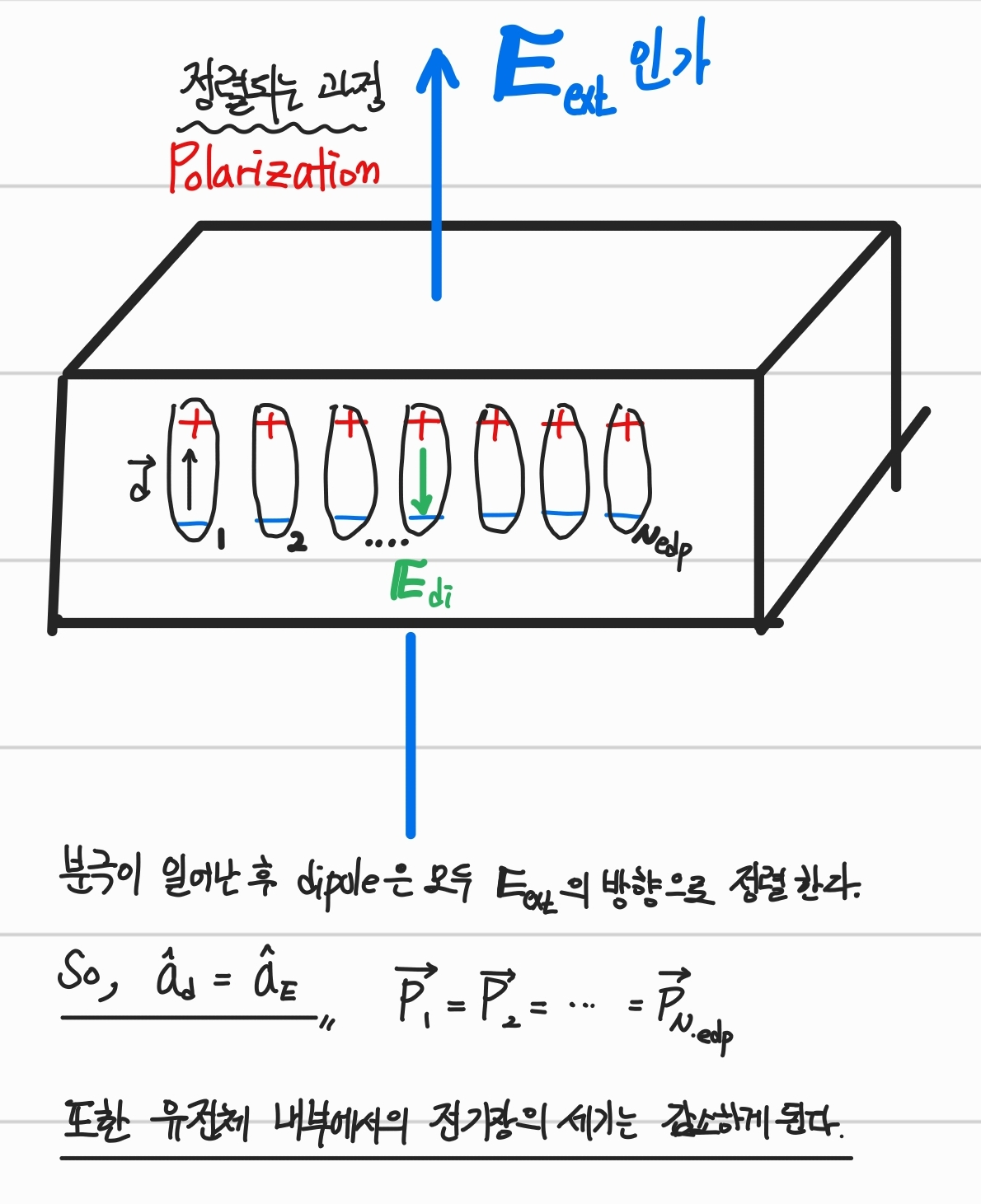
• 전기쌍극자들이 정렬하는 과정을 분극(Polarization)이라고 한다.

• 또한 모든 $i$에 대해 $\mathbf{p_i}$가 같아지므로 분극벡터를 다음과 같이 다시 정리할 수도 있다.
  $\mathbf{p}=Qd\mathbf{a}_E \triangleq\mathbf{p}$
  $\mathbf{P}\triangleq \frac{\displaystyle\sum_{i=1}^{N.edp}\mathbf{p_i}}{\Delta V}=\frac{N_{edp}}{\Delta V}\mathbf{p}=n_{edp}\mathbf{p}=n_{edp}Qd\mathbf{a}_E$

• $n_{edp}=\frac{N_{edp}}{\Delta V}$ 전하 쌍극자 농도:
  단위체적당 전하쌍극자가 얼마나 존재하는 지

• 분극벡터의 크기는 농도가 증가할 수록, Dipole moment가 클수록, 전하쌍극자를 이루는 전하Q의 크기가 클수록, 전하쌍극자의 간격이 클수록 크다.

3) 분극 후의 분극 벡터는 전기장의 세기와 비례한다.

$\mathbf{P} \propto \mathbf{E}$
그 비례상수를 /chi/ 카이 e로 정의한다.

$\mathbf{P}= n_{edp}Qd\mathbf{a}_E=n_{edp}Qd\frac{\mathbf{E}}{|\mathbf{E}|}$ !!

• $n_{edp}=\frac{N_{edp}}{\Delta V}$
• $\mathbf{a}_E=\frac{\mathbf{E}}{|\mathbf{E}|}$

$\mathbf{P}$ 의 단위와 전기장의 세기 $\mathbf{E}$의 단위를 맞춰주기 위해서는 진공에서의 유전율인 $\epsilon_0$를 곱해주면 단위가 맞춰진다고 생각하면 편하다.

$\mathbf{P}=n_{edp}Qd\frac{\mathbf{E}}{|\mathbf{E}|}$
$\mathbf{P} = \chi_e\epsilon_0\mathbf{E}$

• $\chi_e$: 유전체의 전기 감수율(electric susceptibility)
  전기장에 의해서 전기 쌍극자가 줄을 얼마나 잘 서냐로 생각하면 편함.
  전자 재료의 특성이고, 전하쌍극자의 종류에 따라 다르다.
• $\chi_e$ 는 Q와d 즉 $\mathbf{P}$에 비례하고 농도인 $n_{edp}$에도 비례한다.

4) 분극 후의 유전체 내의 전기장의 세기와 상대적 유전율

$\mathbf{D}$는 재료에 무관하고 $\mathbf{E}$는 재료에 영향을 받는 값이다.

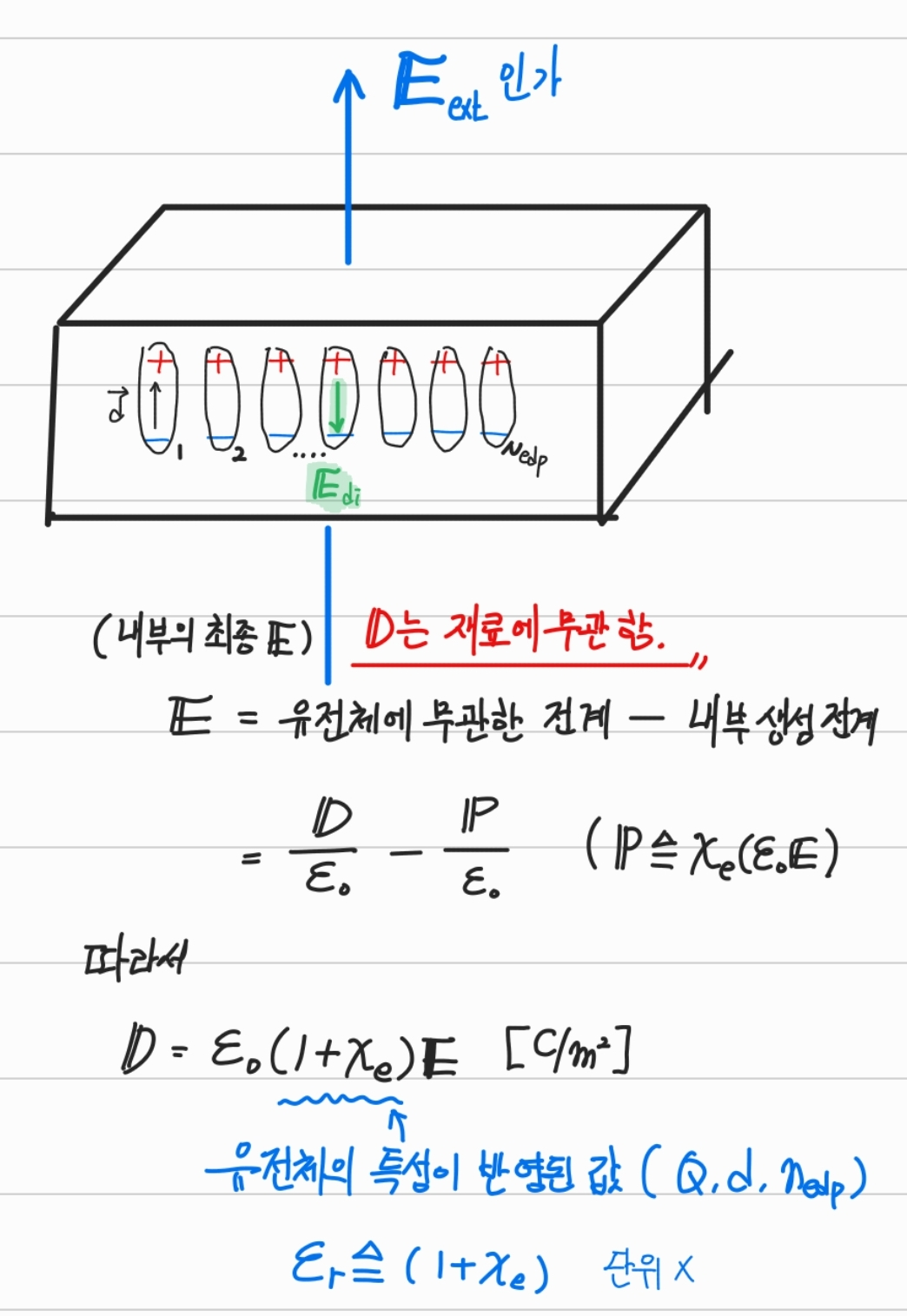
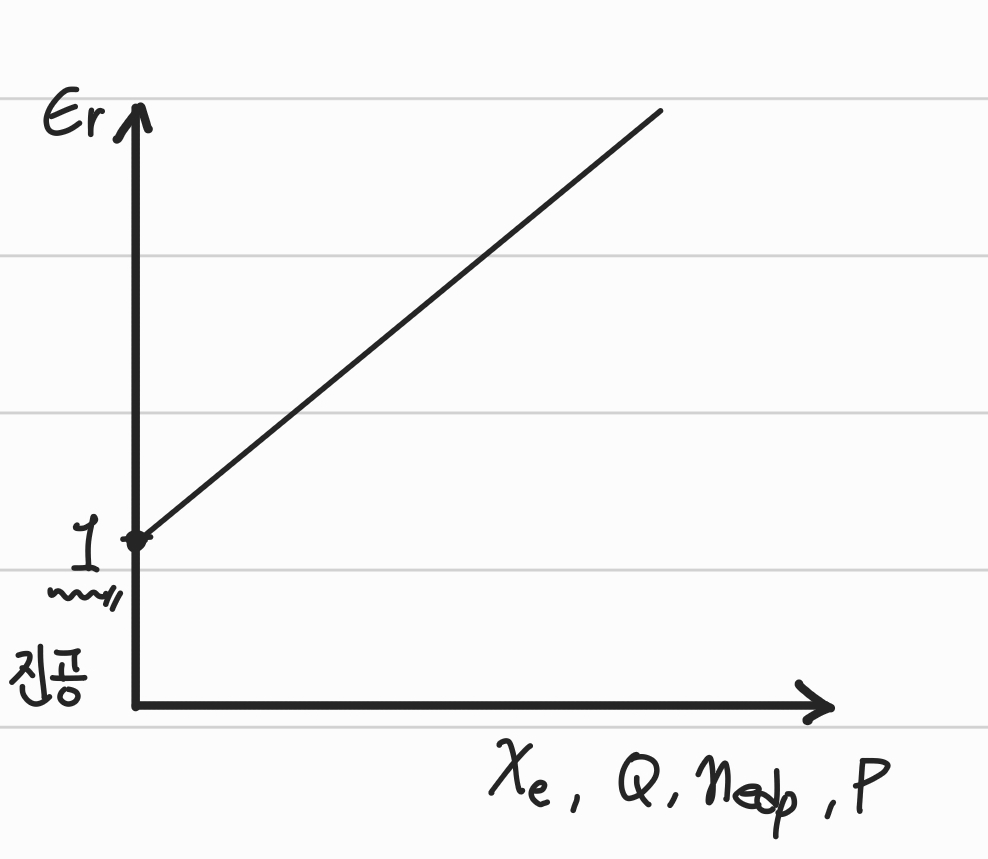
• 유전상수($\epsilon_r$): 외부 전기장에 대한 반응을 나타내는 재료의 특성을 나타내는 것을 통채로 묶어놓은 변수이다!

• $\mathbf{D}=\epsilon_0(1+\chi_e)\mathbf{E} =\epsilon_0\epsilon_r\mathbf{E}$

• 분극에 의해 전하 쌍극자가 정렬되고 이에 따른 전기장은 외부 전기장과 반대 방향이다.

• 

그 외 재료 이야기

5) 일반적인 유전체

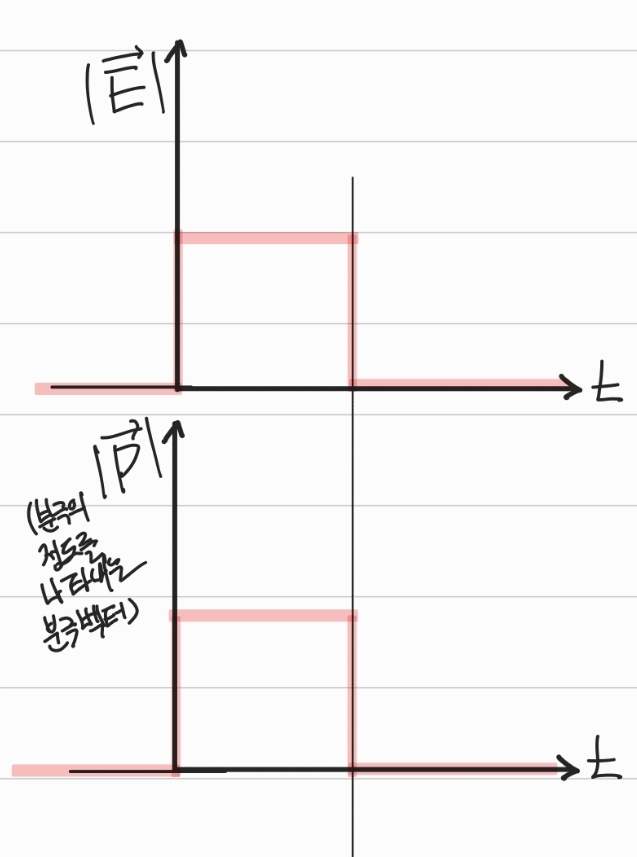
6) 강유전체 memory

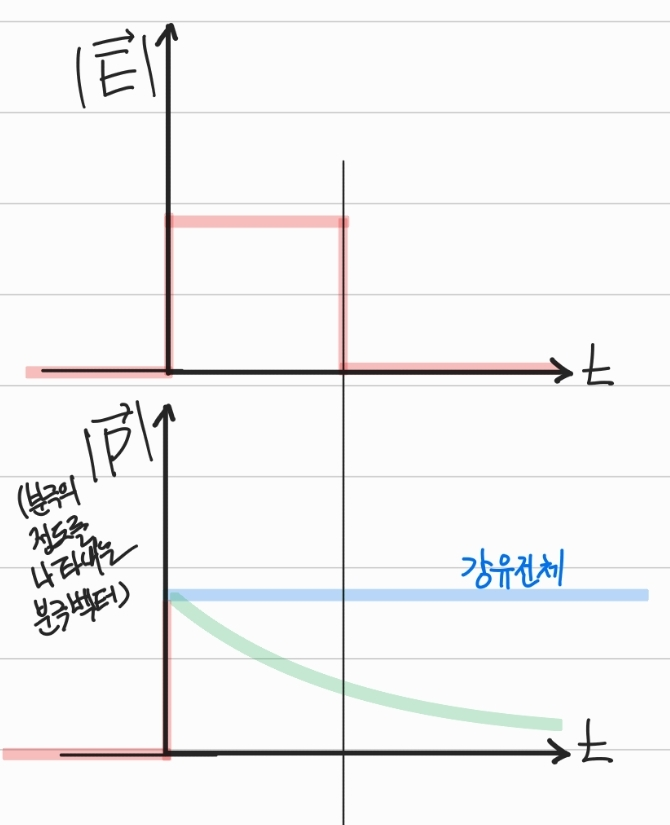
• 나중에 분극이력특성곡선(hysteresis loop)에 대해 이해하는 시간을 가져보겠다.
• Forward sweep과 reverse sweep의 특성이 다른 것을 hysteresis 특성 이라고 한다.