baseline

생성모델들에 대한 수학적 이해를 해보고자 하니 수식적으로 빈 공간이 생겨 위로 위로 올라가다가 시작점을 MLE 개념부터 알아야 겠다는 생각이 들었다. 여러 블로그나 강의자료 글들을 참고하여 가장 이해하기 쉬운 형태로 정리하고자 한다. 여러 예제들이 많은데 레퍼런스를 참

들어가기에 앞서 알면 단순하지만 모르면 헷갈리는 오늘 다룰 내용에서 중요한 개념인 marginalize에 대해서 짚고 넘어가 보자. likelihood function은 관측된 sample을 가지고 모든 가능한 parameters value에 대해 확률을 계산하는 함수

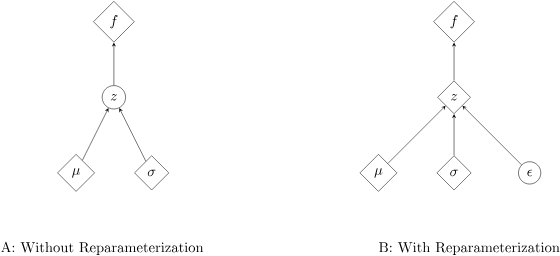
이전 포스팅에선 Variational inference와 ELBO를 다뤘다. 사실 이건 모두 Variational Autoencoder(VAE)를 위해 다뤘다고 해도 과언이 아니다. 오늘 드디어 그 VAE에 대해서 알아보자. VAE VAE는 variational 하

Wassserstain distance는 Earth Mover's distance라고도 불리운다. 이 방법은 WGAN (Arjovsky 2017)에서 사용된 방법으로 생성모델 계보에서도 의미가 있다. 이 방법은 두 확률 분포 간의 사이를 측정하는 방법 중 하나이다. (

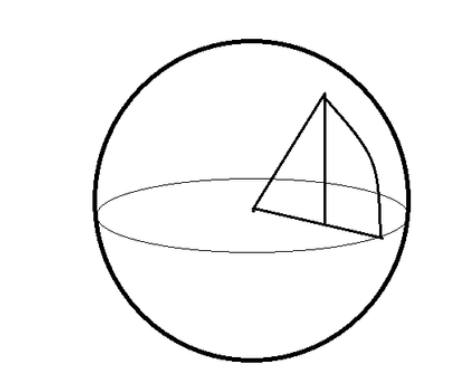
예전에 공부해두었던 것을 블로그로 포스팅softmax처럼 값을 class별로 분류할 때, 크게 4개의 거리를 고민해야 한다.들어가기 전에 geodesic distance란..?쉽게 말해 구의 표면(구면)을 공간으로 하는 두 점을 잇는 최단 경로한글로 된 설명은 여기를

distillation 개념들이 자꾸 논문에서 등장하는데 용어의 개념을 정확하게 모르니까 헷갈려서 간단하게 정리하고자 한다.한 줄로 말하자면 teacher model을 보고 student model을 훈련 시키는 방법teacher가 가진 지식을 student에게 잘 전

Kronecker product는 scalar에 matrix를 곱할 때를 상상하면 쉽게 이해할 수 있다.먼저 scalar와 matrix 곱을 생각해보자. 만약 scalar $a$와 matrix $B$를 곱한다면 다음처럼 쓸 수 있다.$$a \\cdot B = a \\c