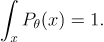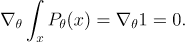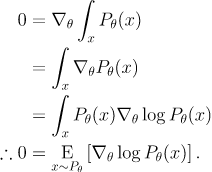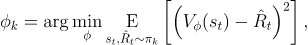Policy Optimization

Intro

이번 챕터에서 우리는 policy optimization algorithm의 수학적 기초에 대해 논의하고, 간단한 에제 코드를 살펴볼것이다. 우리는 Policy Gradient 이론의 핵심 결론 세가지에 대해 이야기 할건데, 이는 다음과 같다.

• 정책 매개 변수에 따른 정책 퍼포먼스의 경사(Gradient)를 설명하는 가장 간단한 방정식(수식)
• 위 수식(방정식) 에서 쓸데없는 terms를 빼버릴 수 있는 규칙
• 위 수식 에서 유용한 terms를 추가할 수 있는 규칙
  그 다음에 우리는 이 세가지 결론을 모두 이용해서 Policy Gradient를 위한 Advantage-Based Expression을 설명 할 것이다(이 최종 수식은 우리가 VPG-Vanilla Policy Gradient를 구현할 때 사용한다.)

Deriving the Simplest Policy Gradient

여기서, 우리는 확률적이고(stochastic) 매개변수화된(parameterized) 정책 $\pi_\theta$을 가정한다. 우리의 목표는 기대수익(expected return) $J(\pi_\theta)=\Epsilon_{\tau\sim\pi}[R(\tau)]$을 극대화 하는걸 목표로 한다.
이 식의 미분을 구하기 위해서, $R(\tau)$를 finite-horizon undiscounted return으로 둘 것 이지만, infinite-horizon discounted return에서의 미분을 구하기 위한 세팅도 거의 동일하다.

우리는 다음과 같이 경사 상승법(Gradient Ascent)를 통해 정책을 최적화 할것이다.

$\theta_{k+1}=\theta_k+\alpha\nabla_\theta J(\pi_\theta)|_{\theta_k}$

정책 퍼포먼스(기대수익)의 기울기(gradient of policy performence) $\nabla_\theta J(\pi_\theta)$는 Policy Gradient라고 불리고, 이러한 방식으로 정책을 최적화 하는 알고리즘을 Policy Gradient Algorithm 이라고 부른다. (예를들어 VPG, TRPO등이 있다. PPO도 Policy Gradient Algo라고 불리지만 엄밀히 말하면 조금 다르다.)

Policy performence: 기대수익, 목표함수, $J(\pi_\theta)$
Policy Gradient: 목표함수의 미분(혹은 기울기, 경사), $\nabla_\theta J(\pi_\theta)$
Policy Gradient Algorithm: 경사 상승법을 통해 정책을 최적화 하는 Algorithm

이 알고리즘을 실제로 쓰기 위해서는 우리는 Policy Gradient에 대한 계산 가능한 수식이 필요하다. 이것은 두가지 단계를 포함하는데, 이는 다음과 같다.

1) 기댓값의 형태를 띄는 목표함수의 해석적 미분값을 구한다음,
2) 유한개의 env-agent steps로부터 나온 데이터들로 계산 가능한 기대 수익의 표본 추정치를 형성한다.(...)

이번 세부항목에서 우리는 이러한 수식의 가장 간단한 형태를 구할것이고, 다음 세부항목에서는 이러한 형태를 실제로 PG 알고리즘 구현에 쓰이는 버전으로 향상 시킬것이다.

해석적 미분(Analytical Gradient)
해석적 미분 방식은 논리적인 전개로 풀 수 있는 문제를 말한다. 반대되는 개념은 수치미분(Numerical Gradient)인데, 모종의 이유(미분 불가능한 함수라거나)로 해석적 미분 방식을 쓸 수 없을때, 수치적 접근을 통해 근사값을 찾는 방식이다.

일단 Analytical Gradient를 미분할때 유용한 몇가지 수학적 Fact를 살펴보자.

1. Probability of a Trajectory
정책 $\pi_\theta$이 주어졌을때, 에피소드 $\tau=(s_0,a_0,...,s_{T+1})$의 확률은 다음과 같다.
$P(\tau|\theta)=\rho_0(s_0)\displaystyle\prod_{t=0}^{T-1}P(s_{t+1}|s_t,a_t)\pi_\theta(a_t|s_t)$

자세한 설명은 여기를 참고.

2. The Log-Derivative Trick
로그 미분 트릭은 $\log x$의 $x$에 대한 미분이 $\frac{1}{x}$이라는 미적분학의 간단한 정리에 기반한다. 이를 재배열하고 chain rule을 통해 통합하면, 우리는 다음과 같은 식을 얻는다.

$\nabla_\theta P(\tau|\theta)=P(\tau|\theta)\nabla_\theta \log P(\tau|\theta)$

3. Log-Prob of a Trajectory
에피소드의 로그 확률은 다음과 같다.
$\log P(\tau|\theta) =\log \rho_0(s_0)+\displaystyle\sum_{t=0}^T(\log P(s_{t+1}|s_t,a_t)+\log \pi_\theta(a_t|s_t))$

4. Gradient of Environment Functions
환경은 $\theta$를 매개변수로 가지지 않기 때문에, $\rho_0(s_0), P(s_{t+1}|s_t,a_t),R(\tau)$의 미분값은 0이다.

5. 4를 이용해서 Grad-Log-Prob of a Trajectory 구하기
$\nabla_\theta P(\tau|\theta)=\displaystyle\sum_{t=0}^T\nabla_\theta\log\pi_\theta(a_t|s_t)$

1~5를 합치면 다음과 같은 식을 도출할 수 있다.

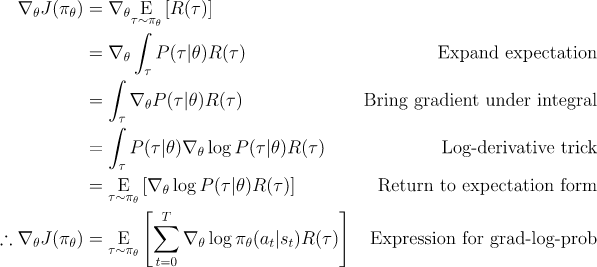
위 식은 기댓값이므로, 표본들의 평균으로 근사할 수 있다. 다시말해, Agent가 정책 $\pi_\theta$를 통해 env에서 행동한 에피소드들 $\mathcal{D}=\{ \tau_i\}_{i=1,2,...N}$을 모은다면, Policy Gradient는 다음과 같이 근사할 수 있다.

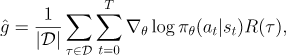
여기서 $|\mathcal{D}|$는 에피소드의 갯수이다.

마지막 수식은 우리가 원하던 '연산 가능한' 수식의 가장 간단한 형태이다. 위 식은 연산이 가능하므로, Agent가 환경에서 정책을 시행한 에피소드를 모으면 우리는 정책을 업데이트 하기 위해 필요한 Policy Gradient를 구할 수 있다.

Implementing the Simplest Policy Gradient

간단한 버전의 Policy Gradient Algorithm을 Pytorch로 구현해본다.

1.Making the Policy Network

# make core of policy network
logits_net = mlp(sizes=[obs_dim]+hidden_sizes+[n_acts])

# make function to compute action distribution
def get_policy(obs):
    logits = logits_net(obs)
    return Categorical(logits=logits)

# make action selection function (outputs int actions, sampled from policy)
def get_action(obs):
    return get_policy(obs).sample().item()

위 코드는 feedforward NN Categorical 정책을 사용하기 위한 모듈과 함수를 만든다.(Categorical Policy가 기억이 안나면 여기를 보세용

logits_net 모듈의 아웃풋은 액션들의 prob과 log-prob을 계산할때 쓰일 수 있고, get_action 함수는 logit값을 기반으로해 액션을 샘플링 한다.

여기서 쓴 get_action 함수는 인자로 하나의 obs만 받는다고 가정하기 때문에 단하나의 요소만을 가지는 텐서의 값을 반환해주는 .item() 을 쓸 수 있다.

위 코드에서 많은 일들이 Categorical object 에 의해 처리된다. 이것은 확률 분포와 관련된 여러가지 수학적 함수들을 가지고 있는 파이토치 클래스이다. 예를들어, 확률 분포로 부터 샘플링을 해주는 함수, 샘플들이 주워졌을때 log-prob을 연산해주는 함수 등을 가지고있다. 매우 유용한 클래스이므로 충분히 숙지하고 잘 사용하자.

logits의 Categorical 분포는 다시 말하면 각각의 결과값들이 logits를 Softmax 함수에 넣어서 나온 확률들이라는 것이다. 수식으로 표현하자면, logit $x_j$의 Categorical 분포는 다음과 같다.

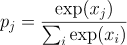
2. Making the loss function

# make loss function whose gradient, for the right data, is policy gradient
def compute_loss(obs, act, weights):
    logp = get_policy(obs).log_prob(act)
    return -(logp * weights).mean()

위 코드는 Policy Gradient Algorithm의 손실 함수이다. 올바른 데이터를 넣었을때, 이 함수의 미분값은 Policy Gradient와 동일하다. 여기서 올바른 데이터란, 현재 정책으로 행동하여 수집된 (state, action, weight) 형식의 튜플이고, weight는 state-action쌍이 속해있는 에피소드의 리턴값이다(후술하겠지만, weight에 리턴값 대신 다른게 들어갈 수 있다.)

우리가 저 함수를 loss function 이라고 부르지만, 이는 지도학습에서 흔히 쓰는 전형적인 손실 함수가 아니다. 일반적인 loss function 과 크게 두가지 차이점이 있는데, 이는 다음과 같다.

1. 데이터 분포가 매개변수에 종속적이다.
손실함수는 보통 우리가 최적화 하려고 하는 매개변수와 독립적인 (y-true 같은)고정값을 기반으로 정의된다. 하지만 여기서는 매개변수에 종속적인 정책을 가지고 데이터를 샘플링 한다.

2. 퍼포먼스를 측정하지 않는다.
손실함수는 보통 우리가 중요로 하는 수치를 평가한다. 예를들어 Regression 모델에서는 우리가 예상한 값과 실제값이 얼마나 비슷한지를 평가한다. PG에서 우리가 중요로 하는 수치는 기대 보상(expected return) $J(\pi_\theta)$ 인데, 우리의 '손실' 함수는 기대보상에 전혀 근사하지 않는다. 그럼에도 불구하고 이 '손실' 함수는 유용한데, 현재의 매개변수와 그로 생성된 데이터로 평가했을때 손실 함수가 퍼포먼스의 음의 그라디언트를 가지기 떄문이다.

하지만 이 Gradient Descent의 첫 스텝 이후에는 더이상 퍼포먼스와 손실함수간의 관계성이 없어진다. 앞에 배운걸 떠올려보자. PG에서의 손실함수는 '현재'의 policy로 행한 데이터로 만들어 진다고 했는데, 한번 매개변수 업데이트를 하고 나면 그 손실함수는 이미 '과거'의 손실함수가 되버린다.(쓰고보니 말장난 같다)
이것은 주워진 배치 데이터로 '손실' 함수를 최소화 하는게 기대 보상을 향상시킨다는 보장이 없다는걸 의미한다. 이 '손실'을 $-\infty$ 로 보낸다 해도 정책의 퍼포먼스는 나아지지 않을것이다. 종종 deep RL 연구원들은 이러한 결과를 배치 데이터에 오버피팅 됐다고 한다. 설명을 위해서 이렇게 말하지만, 이게 일반화의 오류를 말하는건 아님으로 너무 곧이 곧대로 받아들이진 말자.

여기서 이러한 포인트를 짚은 이유는 많은 ML practitioner들이 손실 함수를 트레이닝에서 유용한 시그널이라고 생각하기 때문이다("손실 함수가 작아지기만 하면 된다"는 식으로.) 그러나 PG에서 이러한 생각은 맞지 않다. 우리는 오직 Average Return만 신경 써야한다. 손실함수 자체로는 아무런 의미를 갖지 않는다.

위 코드에서 Categorical의 log_prob 메소드를 사용해 logp 텐서를 만든 방법은 다른 분포(distribution) 객체들을 사용할때 수정이 필요할 수 있다.

예를들어 정규분포를 사용한다면, policy.log_prob(act)의 아웃풋은 각 Vector-Valued 액션의 각각의 성분들을 포함하는 텐서가 될것이다. 다시 말하자면,
인풋의 모양: (batch, act_dim)
아웃풋의 모양: (batch, act_dim)
RL Loss를 만들기 위한 텐서의 모양: (batch,)
가 되는것이다. 이러한 케이스에서 액션의 log-prob를 구하기 위해서는 action-component들의 확률값을 다 더해줘야 한다. 구현 코드는 다음과 같다.

logp = get_policy(obs).log_prob(act).sum(axis=-1)

3. Running One Epoch of Training

# for training policy
def train_one_epoch():
    # make some empty lists for logging.
    batch_obs = []          # for observations
    batch_acts = []         # for actions
    batch_weights = []      # for R(tau) weighting in policy gradient
    batch_rets = []         # for measuring episode returns
    batch_lens = []         # for measuring episode lengths

    # reset episode-specific variables
    obs = env.reset()       # first obs comes from starting distribution
    done = False            # signal from environment that episode is over
    ep_rews = []            # list for rewards accrued throughout ep

    # render first episode of each epoch
    finished_rendering_this_epoch = False

    # collect experience by acting in the environment with current policy
    while True:

        # rendering
        if (not finished_rendering_this_epoch) and render:
            env.render()

        # save obs
        batch_obs.append(obs.copy())

        # act in the environment
        act = get_action(torch.as_tensor(obs, dtype=torch.float32))
        obs, rew, done, _ = env.step(act)

        # save action, reward
        batch_acts.append(act)
        ep_rews.append(rew)

        if done:
            # if episode is over, record info about episode
            ep_ret, ep_len = sum(ep_rews), len(ep_rews)
            batch_rets.append(ep_ret)
            batch_lens.append(ep_len)

            # the weight for each logprob(a|s) is R(tau)
            batch_weights += [ep_ret] * ep_len

            # reset episode-specific variables
            obs, done, ep_rews = env.reset(), False, []

            # won't render again this epoch
            finished_rendering_this_epoch = True

            # end experience loop if we have enough of it
            if len(batch_obs) > batch_size:
                break

    # take a single policy gradient update step
    optimizer.zero_grad()
    batch_loss = compute_loss(obs=torch.as_tensor(batch_obs, dtype=torch.float32),
                              act=torch.as_tensor(batch_acts, dtype=torch.int32),
                              weights=torch.as_tensor(batch_weights, dtype=torch.float32)
                              )
    batch_loss.backward()
    optimizer.step()
    return batch_loss, batch_rets, batch_lens

train_one_epoch() 함수는 PG의 한 에폭을 실행하는데, 그 절차는 다음과 같다.

1. agent가 가장 최신의 Policy를 사용해 environment에서 경험 데이터를 모으는 단계
2. Policy Gradient를 딱 한번 업데이트 해주는 단계

알고리즘의 메인 루프는 반복적으로 train_one_epoch() 를 호출한다.

Expected Grad-Log-Prob Lemma

이번 subsection 에서는 우리는 PG 이론에 굉장히 자주 쓰이는 중간 결과식을 도출 할 것이다. 그리고 이를 EGLP Lemma라고 부를것이다.

EGLP Lemma
$P_\theta$가 임의의 변수 $x$에 관한 매개확률변수일때, 다음이 성립한다.

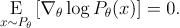
증명

먼저, 모든 확률 분포는 정규화돼있다.

양변을 $\theta$에 관해 미분하면 다음과 같다.

로그 미분 트릭을 이용해서 식을 전개하면 다음식을 얻을 수 있다.

Don’t Let the Past Distract You

위에서 얻은 PolicY Gradient 수식을 다시 한번 살펴보자

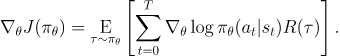
위 그라디언트를 사용해서 parameter update를 진행하면 각각의 action의 log-prob은 모든 reward의 합인 $R(\tau)$에 비레해 증가(혹은 감수)될 것이다. 직관적으로, 이건 말이 안된다.

Agent는 각 action을 강화 시킬때 그 action의 결과만을 근거로 해야한다. action을 취하기 전에 발생한 reward는 그 action이 얼마나 좋은지에 아무런 관련이 없다.

이러한 직관은 수학적으로도 표현 가능하며, 따라서 Policy Gradient는 다음과 같이도 표현될 수 있다.

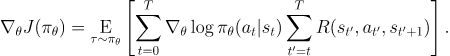
위 식에서는 action들은 오직 각각의 action 이후의 reward만을 근거로 해서 강화된다. 우리는 이를 "reward-to-go policy gradient" 라고 부른다.

수학적 증명은 귀찮아서 생략하겠다. 직관적으로 와닿는 부분이기도 하고, openai에서 걸어놓은 증명 링크도 망가져있다. 그렇다고 내가 직접 하기에 나는 너무 게으르다

reward-to-go 는 파이썬에서 다음과 같이 손쉽게 구현할 수 있다.

def reward_to_go(rews):
    n = len(rews)
    rtgs = np.zeros_like(rews)
    for i in reversed(range(n)):
        rtgs[i] = rews[i] + (rtgs[i+1] if i+1 < n else 0)
    return rtgs

왜 이게 더 좋나?

PG에서 주요한 문제는 저분산 표본 추정치를 얻기 위해 얼마나 많은 Trajectories가 필요한가이다. 과거 보상까지 현재의 액션을 강화하는데 쓰인 처음의 공식에서 평균은 0 이었지만, 분산은 그렇지 않았다. 결과적으로 이는 Policy Gradient의 표본 추정치에 노이즈만 더해준 꼴이다. 이를 제거함으로써, 우리는 필요한 trajectories의 수를 줄였다.

Baselines in Policy Gradients

EGLP lemma에 의해서, State에만 의존적인 어떠한 function b에 대해 다음이 성립한다.

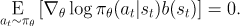
이러한 성질은 PG $\nabla_\theta J(\pi_\theta)$ 에 대한 수식에서 어떤 숫자나 형태를 더하거나 빼는걸 가능하게 한다.

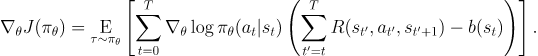
이런식으로 쓰여지는 어떤 함수 b를 baseline 이라고 한다.

Baseline 으로 쓰이는 가장 대표적인 함수가 Value Function $V^\pi(s_t)$ 이다.
실증적으로, 이러한 선택은 PG의 표본 추정치에 분산을 줄여주는 효과가 있다. 이건 결과적으로 더 빠르고 안정적인 정책 학습을 가능하게 한다. 이론적인 시각에서도 'agent가 예상한 대로 행동 했다면, 거기에 대해 Neutral하게 느껴야 한다'는 직관과 합치한다.

실전에서 $V^\pi(s_t)$를 정확하게 계산할 수 없으므로 근사시킨다. 이러한 작업은 보통 인공신경망 $V_\phi(s_t)$를 통해 이뤄지는데, 이 신공망은 정책 네트워크와 동시에 업데이트
된다(그래야 Value Network가 항상 최신의 정책의 Value function을 근사할 수 있다.)
$V_\phi(s_t)$는 보통 다음과 같은 loss-function 을 통해 업데이트 된다.

$V^\pi(s_t)$ 외에도 Advantage나 Td-error등 여러가지 함수를 base function으로 사용하곤 하는데, 근간이 되는 개념은 동일하므로 생략하겠다.

Conclusion

드디어 openAI spinning up - Introduction to Rl 의 번역 및 개념정리가 끝났다. 후반으로 갈수록 너무 귀찮아서 대충대충 해버린 감이 있는데, 그래도 개인적으로는 공부가 많이 됐다. 혹시라도 이 글을 보는 사람들에게도 도움이 됐으면 하는 바람이다.