1. Error Metric?
대학에서 학생을 고르기 위해 학생이 공부를 얼마나 잘 하는지를 평가하듯,
우리가 예측 모델을 고를 때에도 예측 모델이 얼마나 잘 예측하는지 평가할 필요가 있다.
"A 학생이 B 학생보다 공부를 잘 해, 왜냐면 A학생은 표준점수 합이 540점인데, B 학생은 530점이거든!" 이라고 말 할 수 있는 것 처럼,
"A 모델이 B 모델보다 성능이 좋아! 왜냐면 A 모델의 MSE는 XXX 인데 B 모델의 MSE는 YYY거든!" 이라고 말할 필요가 있다는 것이다.
이번 글에서는 모델, 특히나 예측 모델의 오차를 평가할 때 쓰이는 지표들(Error Metric)에 대해 얕게나마 알아보고 생각해 보려고 한다. 가장 유명한(?) R Square 값에 대해서 먼저 쓸까 하는 생각도 했으나, 관련해서는 할 말이 좀 많아서 이후에 조금 더 긴 글을 써 보는걸로...
2. M(???)E
이 글에서 정리해 보려고 하는 Metric 들은 전부 M(어쩌고 저쩌고)E 의 형태를 띈 형태들이다. 여기서 M 은 Mean, E는 Error의 약자이다. 즉, 이 글에서 정리해 보려고 하는 Error Metric들은 오차에 어떤 짓을 한 것들의 평균, 얼마나 많이 틀렸는지에 대한 숫자들이다. 당연히 조금 틀린게 더 좋은 모델이므로, 더 작은 M(???)E를 갖는 모델이 더 나은 모델일 것이다.
(0) Error, 오차.
오차에 대한 얘기 없이 오차 Metric을 정리하면 안 될 것이다. 오차에 대한 사전적 정의는 참값과 근삿값의 차이이다. 오차라는 단어가 주는 느낌적인 느낌 때문에, 오차는 충분하게 모델의 전반적인 성능을 측정할 수 있는 지표일 것 같지만 안타깝게도 오차만으로는 모델의 전반적인 성능을 지표로 쓰이기엔 모자람이 많다.
우선, 오차는 참값-근삿값 대응 하나에 대해 하나가 생긴다. 10개의 참값과 그에 해당하는 10개의 근삿값이 있다면, 오차도 10개가 있게 된다. 그래서 특수하지만 상식적인 방법으로 이를 요약해야 한다.
너무 일반적인 경우(합, 이를 참값 개수로 나누면 평균)으로 오차들을 요약하게 되면 아주 큰 문제가 생기는데,
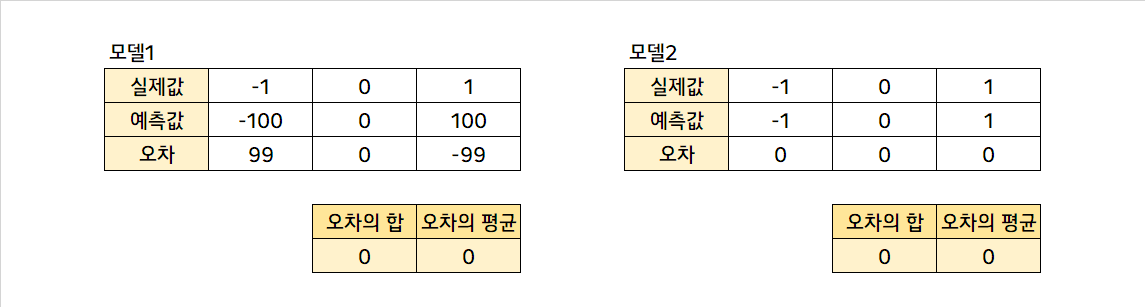
위와 같은 경우가 생길 수 있다. 모델1은 정말 말도 안되는 모델이고, 모델2는 정말 기가막힌 모델인데 그 둘의 오차의 합, 오차의 평균은 모두 0이다. 이 때 오차의 합(또는 평균)만으로 모델을 평가하거나 비교하는건 큰 무리가 있다. 따라서, 오차를 그냥 평균할 것이 아니라 어떤 작업을 한 후에 평균을 냄으로써 모델의 전반적인 오차를 파악해야 하고, 파악할 수 있다.
(1) MAE, Mean Absolute Error, 평균 절대 오차.
위에서 본 예시와 같이 참값의 평균과 근삿값의 평균이 같은 경우, 오차의 합은 이러나 저러나 0이 된다. 이를 해결하는 방법 중 하나로, 오차에 절댓값 함수를 적용시켜 평균을 구하는 방법이 있다. 오차 절댓값들의 평균을 평균 절대 오차, MAE라고 한다.
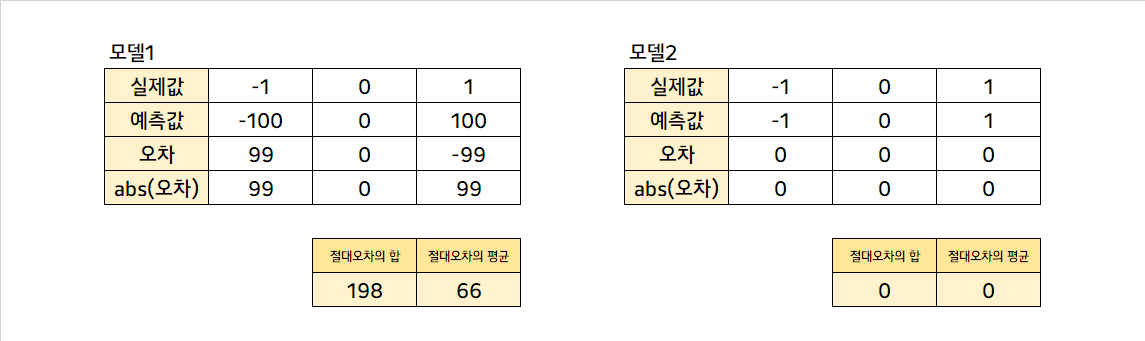
위에서 보았던 말도 안되는 모델과 기가 막힌 모델의 평가가 MAE를 활용하여 상대적으로 상식적으로 이루어졌음을 볼 수 있다. 절댓값을 씌워 오차를 모두 양수로 바꾸고, 그로써 오차의 합이 0이 되는 문제를 보정해주었기 때문이다. 그런데 이런 경우를 생각해 볼 수가 있다.
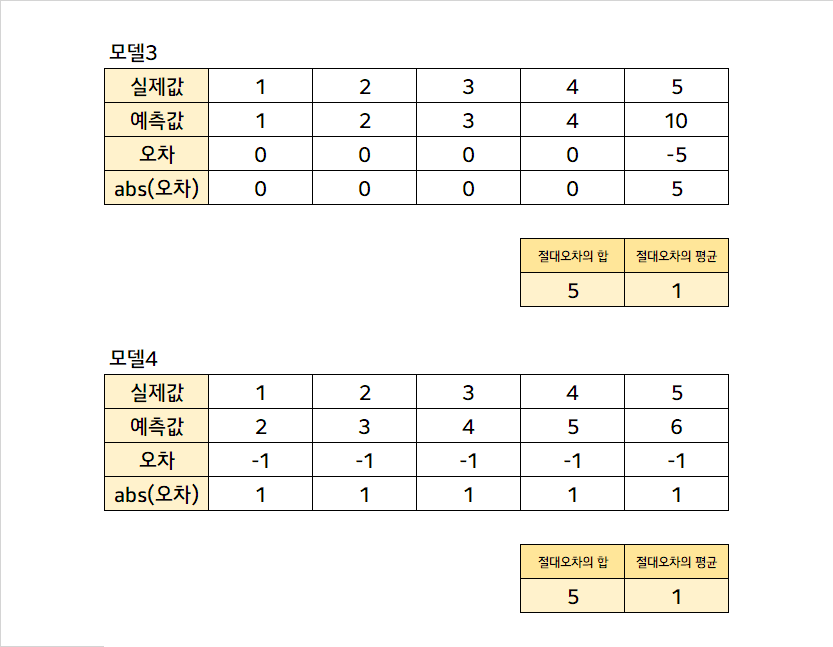
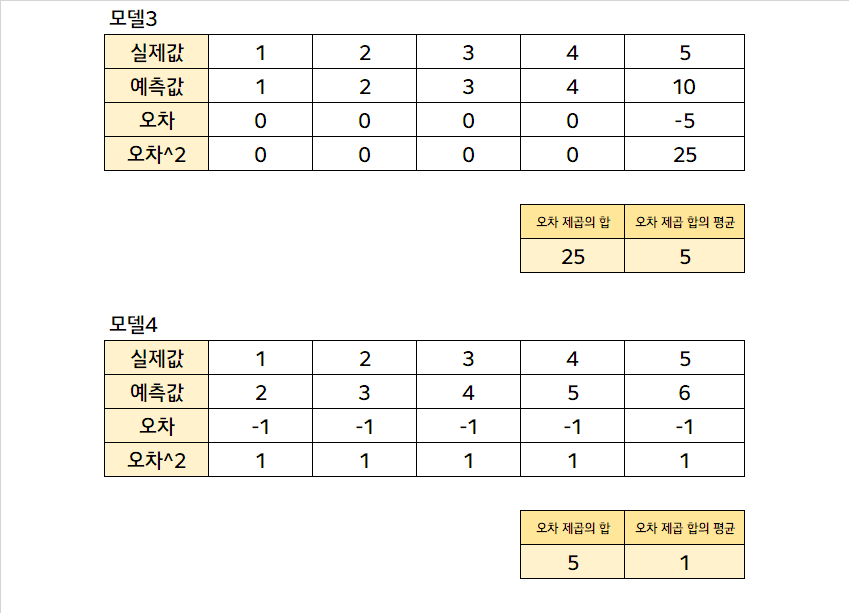
다섯 개의 실제값 중 하나를 엄청나게 틀린 모델3과 다섯 개의 실제값을 모두 조-금 틀린 모델4가 있는데, 이 둘의 MAE는 같다. 이런 경우 모델 3과 모델 4가 같은 정도의 성능이라고 할 수 있을까? 경우에 따라선 그럴 수도 있겠지만, 아닌 경우도 있을 것이다.
(2) MSE, Mean Squared Error, 평균 제곱 오차
얼마 전 독일금리 DLS가 사회적으로 큰 파장을 일으켰다. 독일 금리가 예상 가능한 수준을 크게 벗어나면 벗어날수록 큰 손실을 일으키는 상품이었다고 한다. 이런 때에 실제 금리 예측 모형을 위에서 말한 MAE 기준으로 평가하면 큰 문제가 있을 것이다. 이런 때에, 큰 오차를 더 크게, 작은 오차를 더 작게 만드는 방법이 있는데, 우리가 좋아하는 제곱이다.
1보다 큰 두 수의 경우, 제곱하면 그 둘의 차이는 더 확대된다. 이런 점을 활용하여 오차를 제곱하여 평균한 값, MSE가 종종 활용된다. 그리고 오차를 제곱한 값이기 때문에, 오차가 일반적으로 이 정도다~ 라고 말하기엔 다소 왜곡된 값인데, 따라서 이의 제곱근인 RMSE가 오차에 대한 지표로 활용된다.
(3) MAPE, Mean Absolute Peracentage Error, 평균 절대 비율 오차
그런데, 이런 경우를 또 생각해볼 수가 있다.
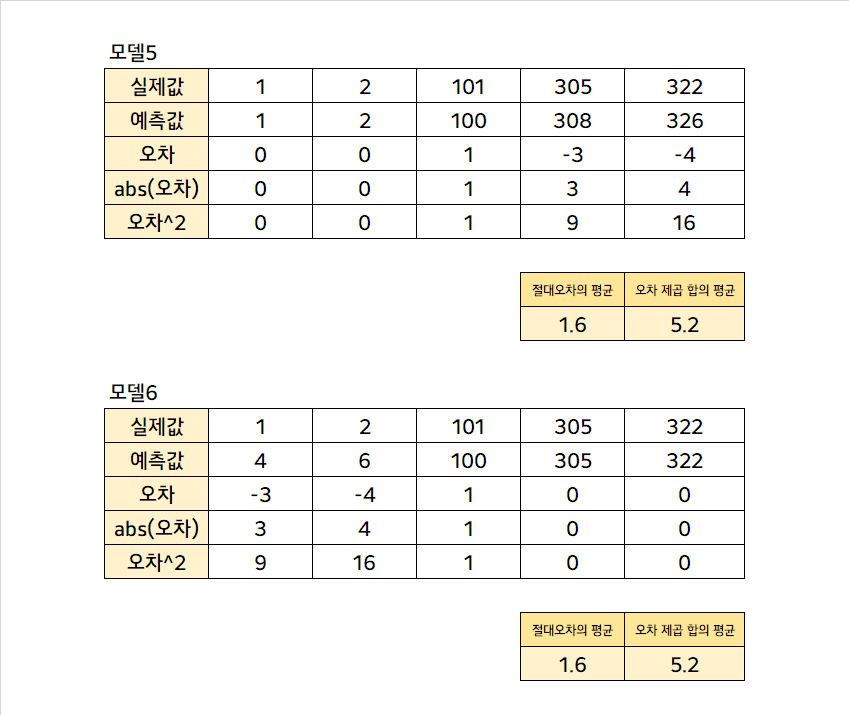
모델 5나 모델 6은 MAE와 MSE가 같은 값이다. 실제로 같은 양의 오차를 갖고 있어서 정말 같은 성능을 내는 모델로 보이나, 관측치 하나 하나를 자세히 보면 사실 사뭇 다르다. 단편적으로 모델 6에서 실제값 1을 4로 예측했는데, 이는 1 입장에서 보면 자신을 4배나 확대해서 예측한 것이다. 그리고 모델 5에서 실제값 305를 308로 예측했는데, 1을 4로 예측한 것과 같은 오차이지만, 305 관점에서는 사소한 (0.98%,3/305) 오차이다. 이와 같이 예측 대상의 Scale이 다양한 경 실제값에서 오차가 얼마나 많은 비율을 차지하는지를 계산하고, 그의 절댓값의 평균을 구한 평균 절대 비율 오차가 종종 사용된다.
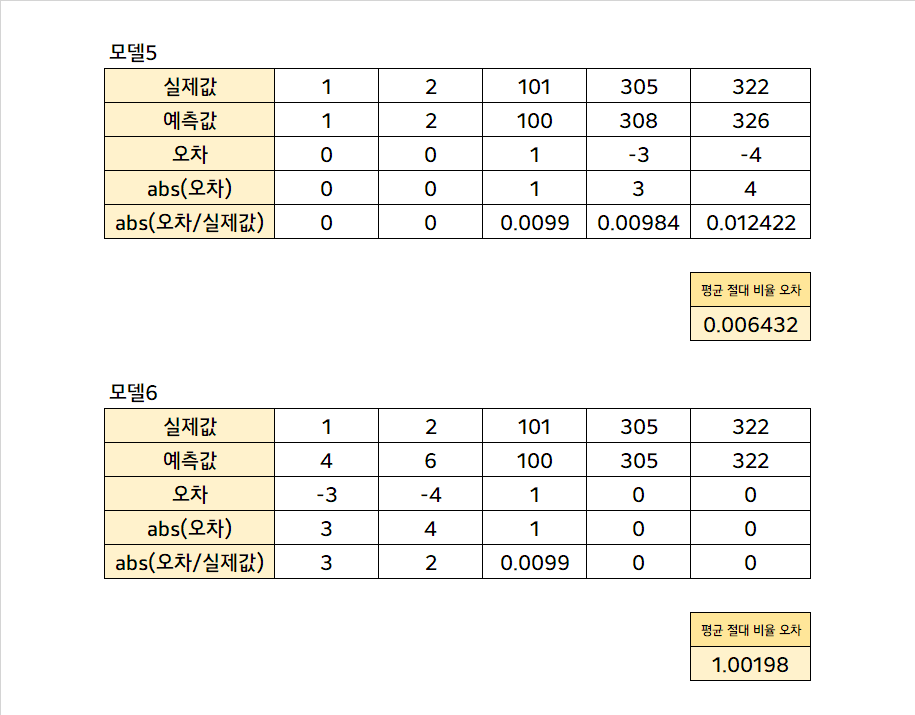
위와 같이, 오차의 비율이 상대적으로 적은 모델5가 모델6보다 더 작은 MAPE를 갖는 것을 볼 수 있다. 단, MAPE의 경우 치명적인 문제가 있는데, 실제값이 0에 가까울수록 오차의 비율이 커진다는 것이고, 실제값이 0인 경우 MAPE 자체를 계산할 수가 없다는 것이다.
3. 결론
어떤 Error Metric이 더 좋냐고 묻는다면, 당연히 정답은 없다. 어떤 문제를 해결해야 하는 지에 따라 다른 Error Metric을 사용해야 하기 때문이다. 문제 해결을 위한 모델 선정에서 어떤 Error Metric을 쓸지 결정하는 것은, Error Metric 뿐 아니라 문제 자체를 이해하지 않고는 불가능할 것이다. 데이터 분석가든, 컨설턴트든, 예측 모델 개발자든, 문제를 해결해야 하는 입장에서 문제를 자세히 들여다 보고 어떤 Error Metric을 사용할지 고민하고 결정해 보자.
+쓰다보니 통계학, 수학 얘기를 거의 않고 글을 썼는데, 조만간 R square 얘기를 하면서 이에 대해 다루면 좋을 것 같다.