
트리 관련 알고리즘 문제를 풀고 싶어도, 트리를 저장할 방법조차 모른다면 트리의 순회나 탐색을 알아도 쓸모가 없다.
트리가 우수수 주어질 때, 어떻게 저장해야 하는지 알아보자.
트리의 표현
트리를 저장하는 방법은 여러 가지가 있다.
트리의 정의에 충실하여 저장하는 방법, 트리의 특징을 이용하여 저장하는 특징, 특정 트리에서만 사용할 수 있는 방법 등이 있다.
연결 리스트를 이용하기
트리는 그래프의 일종이기 때문에, 그래프의 표현 방법과 같이 연결 리스트로 저장할 수 있다.
이때, 트리의 경로는 방향이 있는 것이 아니기 때문에 양방향 그래프를 저장하는 방법을 사용하면 된다. 또한, 어떤 노드의 부모 노드를 아는 것은 전체 그래프에 대하여 다음과 같이 BFS나 DFS 탐색을 한 번 돌리면서 부모를 모두 저장하게 하면 그 다음부터는 바로바로 부모 노드에 접근할 수 있다.
void BFS(vector<int> *node, int V, int *level, int *parent, int start)
{
queue<int> q;
bool check[V + 1] = {false};
level[start] = 0;
parent[start] = -1;
check[start] = true;
q.push(start);
while (!q.empty())
{
int now = q.front();
q.pop();
for (int i = 0; i < node[now].size(); i++)
{
int next = node[now][i];
if (!check[next])
{
level[next] = level[now] + 1;
parent[next] = now; // 부모 노드의 정보를 저장
check[next] = true;
q.push(next);
}
}
}
}연결 리스트로 저장하라고 하면 ?? 그럼 트리 왼쪽 자식 노드랑 오른쪽 자식 노드는 어떻게 접근해 라는 생각이 들 수도 있다. 물론 단순 연결 리스트로는 자식 노드의 방향을 구분하지 못한다.
하지만, 오른쪽 자식 노드와 왼쪽 자식 노드가 구분되어 있다는 것은 해당 트리가 이진 트리라는 것을 말한다. 이진 트리는 이진 트리에서 사용할 수 있는 쉬운 방법을 이용하면 된다.
결론적으로는 항상 연결 리스트를 이용하라는 것이 아니라, 연결 리스트를 이용하여 트리를 저장할 수도 있다는 것을 기억하라는 것!
트리의 부모만 저장하기
트리는 부모 노드가 항상 한 개로 정해져 있으니, 자신의 부모를 저장하는 방법으로도 트리를 저장할 수 있다.
이 방법의 장점은 임의의 노드의 부모 노드가 무엇인지는 바로 찾을 수 있다. 배열의 값이 부모 노드 번호이기 때문이다.
그러나, 임의의 노드의 자식 노드를 찾는 것은 비효율적이다. i번 노드의 자식을 찾기 위해서는 배열의 값이 i인 것을 찾아야 하므로, 배열 전체를 탐색해야한다.
이진 탐색 트리의 표현 방법
배열의 index를 이용하기
이진 탐색 트리는 자식 노드가 최대 2개인 트리이다. 따라서, 어떤 노드가 x일때 자식 노드는 다음과 같이 x를 이용한 수식으로 나타낼 수 있다.
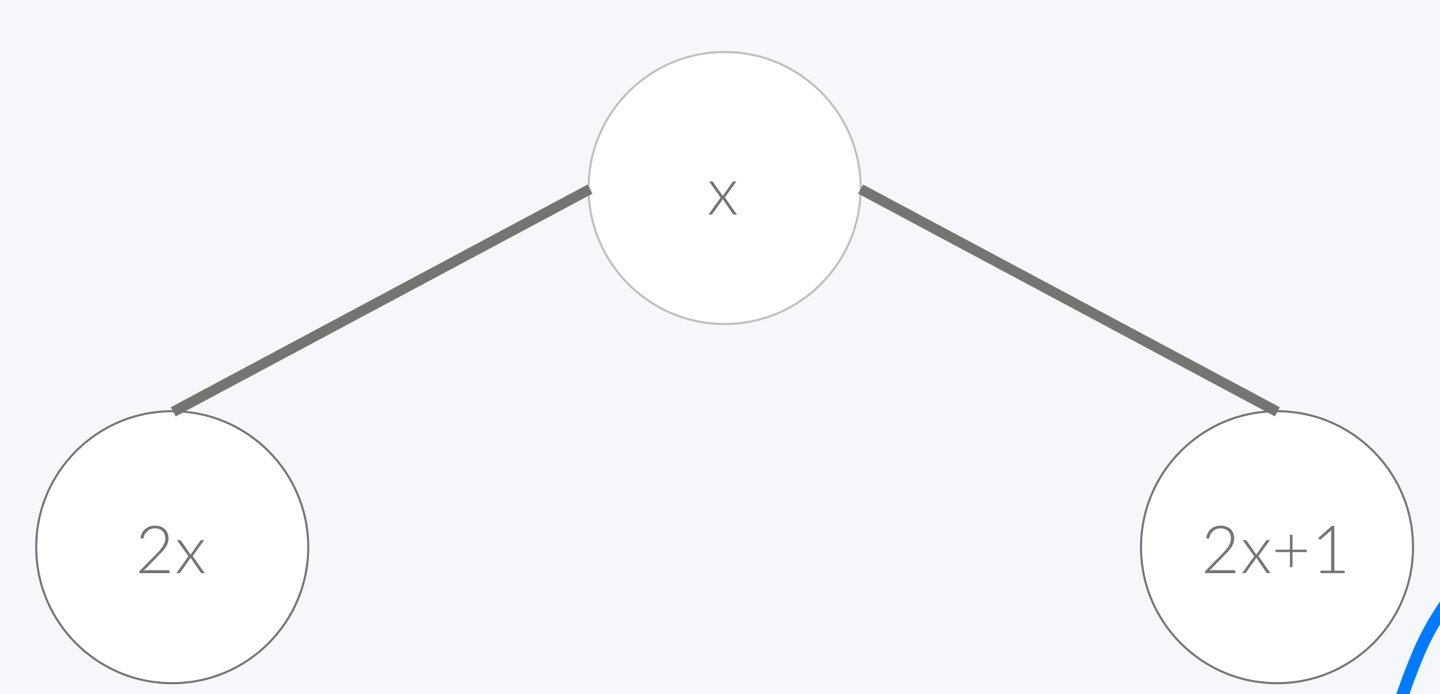
이 방법을 이용하게 되면 배열의 index를 이용하기 때문에, 노드들이 오른쪽 자식 노드만 가지고 있는 skewed tree인 경우에는 쓸데없이 필요한 배열의 크기가 늘어날 수 있으므로 비효율적이다.
이 방법은 이진 트리 중, node가 왼쪽부터 차곡차곡 채워지는 complete binary tree에 적용해야 공간의 낭비 없이 효율적으로 저장할 수 있다.
이차원 배열 이용하기
i번째 노드의 왼쪽 자식은 arr[i][0]에, 오른쪽 자식은 arr[i][1]에 저장하는 방법을 이용할 수 있다.
