퍼셉트론의 어떠한 노드에서의 출력 값을 간략화하면 y = f(wx+b) 정도로 표현할 수 있는데 여기서 f가 활성화 함수이다. weight를 곱하고 bias를 더한 후에 일정한 threshold에 따라 최종 출력이 결정되는 것이다.
Sign
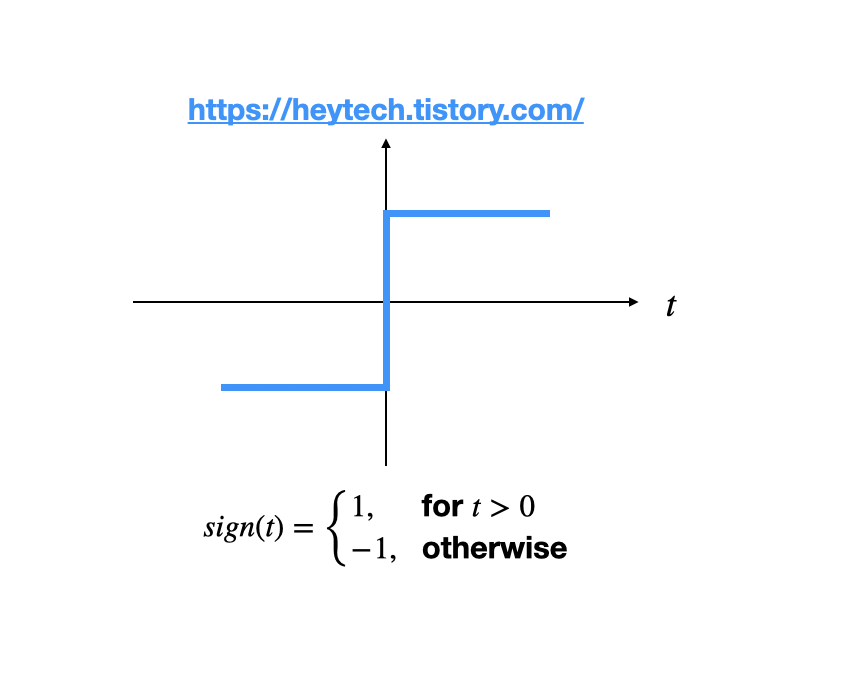
위와 같이 단순히 0보다 크냐 작냐로 임계 처리를 할 수도 있다. 다만 이 경우에는 '얼마나' 라는 개념이 없다. 단순히 나눌 뿐이다.
일반적으로 사용되는 활성화 함수는 아니다.
Sigmoid
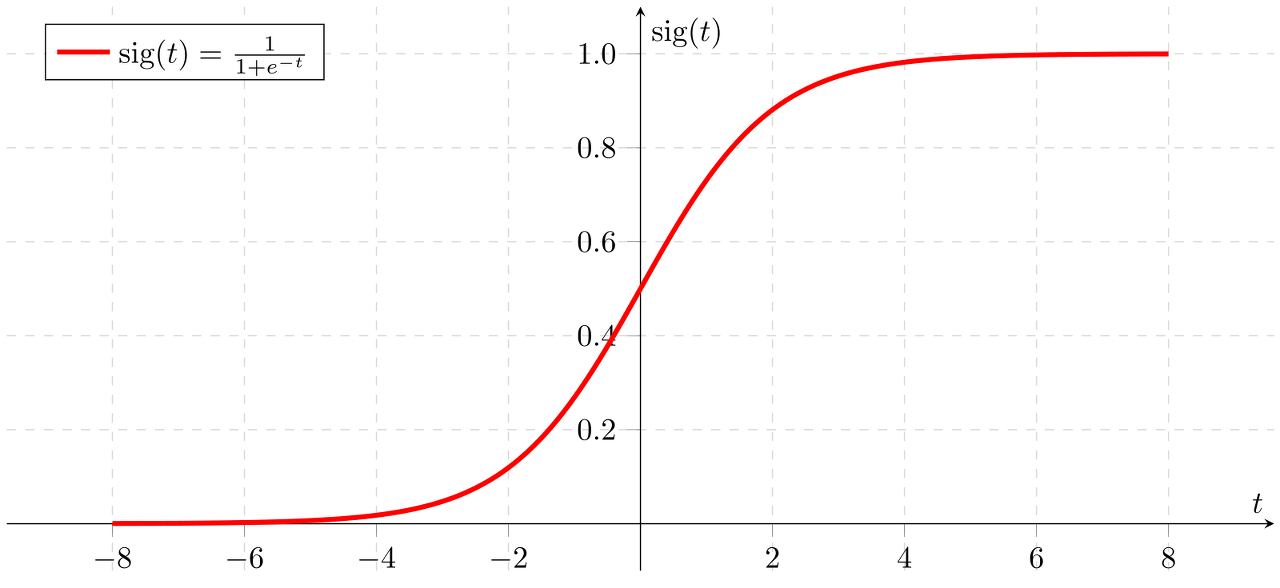
시그모이드는 계단 형태가 아니라 곡선이므로 얼마나 가깝고 머냐에 대한 개념이 있다. 즉 binary가 아니라 실수형태로 표현이 되는 것이고, 0~1 사이의 확률 값으로 표현할 수도 있다.
Binary-class Classification에 주로 사용된다.
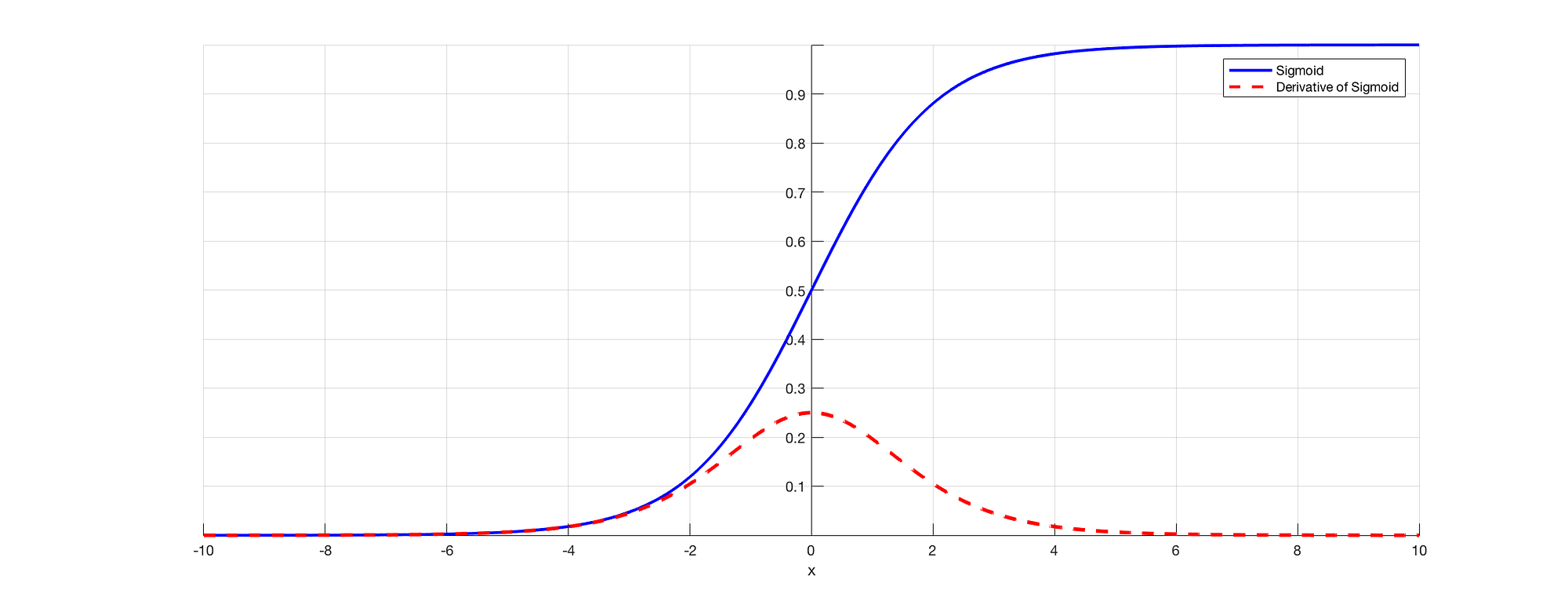
다만 미분할수록 기울기 값이 소실되는 vanishing gradient 문제가 있다.
위와 같이 미분할수록 점차 값이 낮아지는 분포를 가진다.
Softmax
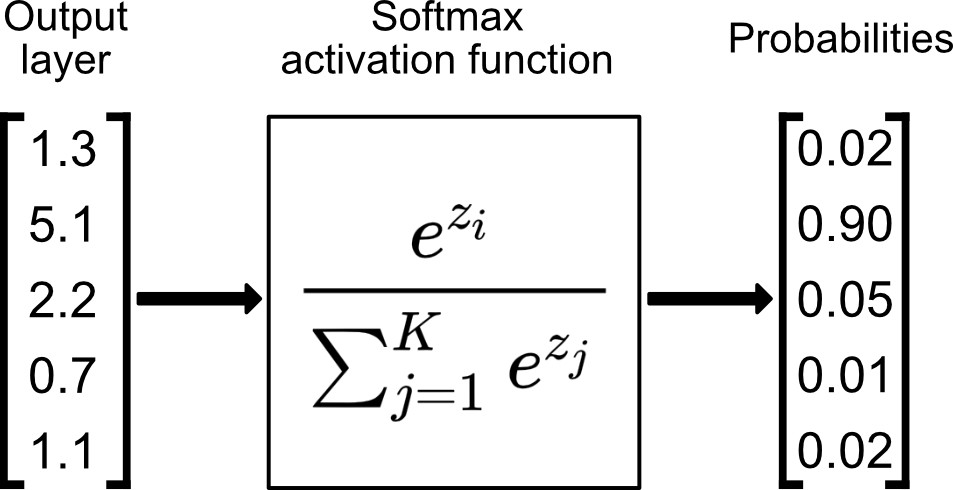
Softmax 함수는 입력을 N개의 출력으로 만들어주고, 각 출력 값은 0~1 사이의 값을 가지며, 모든 값의 합은 반드시 1이 된다.
이러한 특성 때문에 Multi-class Classification에 주로 사용된다. 가장 높은 score를 가지는 argmax class가 정답이 되는 것이다.
ReLU

y=x (x>0) 이고 0 (x<0) 꼴의 함수이다.
sigmoid나 tanh에서의 vanishing gradient 문제를 해결하였으며, 비선형성을 줄 수 있고, 함수 형태가 단순하여 연산 효율성도 좋다. 사실상 대부분의 레이어에서 Relu를 activation function으로 많이 사용한다.
https://for-data-science.tistory.com/68
Leaky ReLU
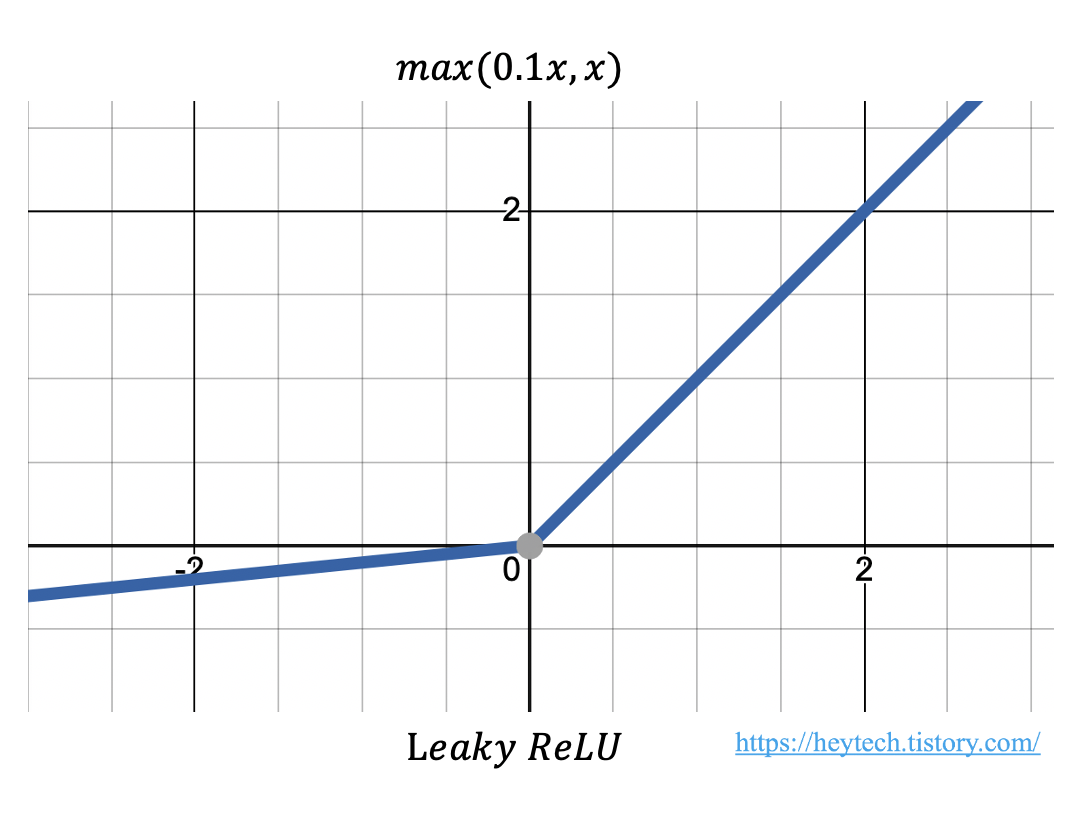
relu는 음수에서 0이 되어버리는 dying relu현상이 있다. 그래서 음수에서도 0이 아닌 매우 작은 값이라도 출력하도록 변형한 것이다.
기타
- PReLU
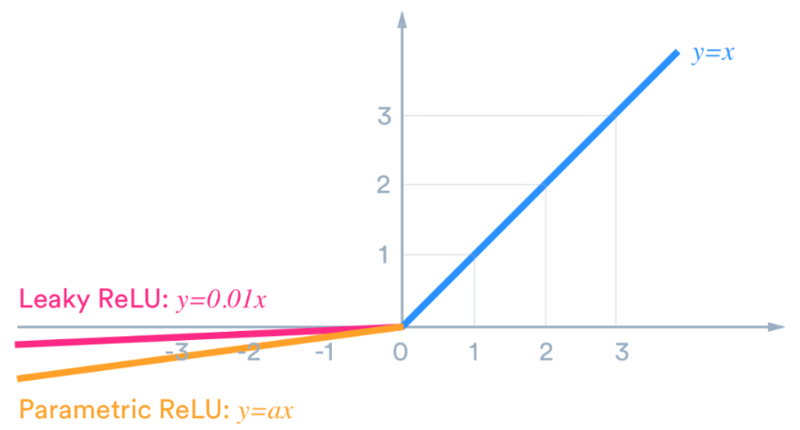
- ELU
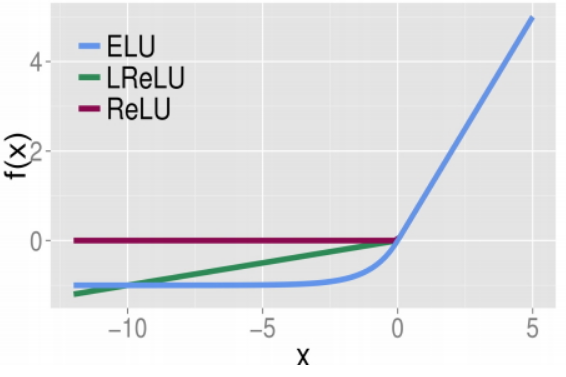
- Maxout
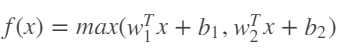
SiLU (Swish)
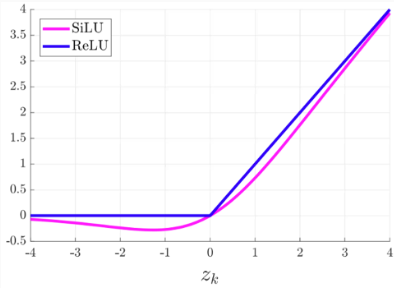
- ReLU보다 성능이 훨씬 좋다고 한다.
- 음수에 대해 바로 0으로 수렴하지 않되, 너무 큰 음수에 대해서 0으로 수렴
- 양수에 대해서 완전한 직선이 아닌 약간의 곡선 형태를 지님 (Non monotonicity)
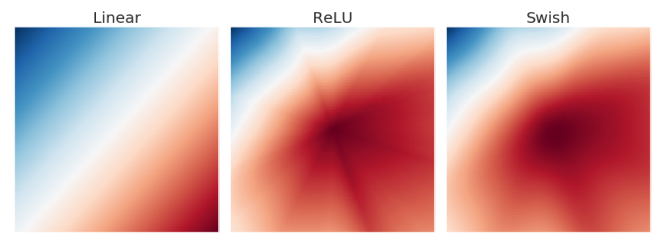
Activation Map을 그렸을때 ReLU에 비해 완만한 변화를 가져서 작은 변화에는 작게, 큰 변화에는 크게 반응하게 해주는 효과가 있다고 한다.
실제 사용
- 일반적인 레이어에서의 활성화 함수 : ReLU
- Multi Label Classification : Softmax
- Binary Label Classification : Sigmoid
- 그 외 : 직접 모델 구성시 적용할 때도 있지만, 대부분 오픈소스 모델에서 이미 적용된 경우가 많다.
참고
- 참고 자료 : https://heytech.tistory.com/360