TIL

오늘은 numpy실습을 하며, 정리할 필요를 느낀 부분에 대해 기록하려합니다. 소주제는 소제목을 참고하면 되겠습니다.

✍️np.dot() 와 np.matmul()

행렬곱을 할 때 수행할 수 있는 연산으론 np.dot()과 np.matmul(),@가 있습니다. np.matmul()와 @은 같다고 생각할 수 있겠습니다.

벡터(1차원 Array)끼리 연산 시, 이는 하나를 열벡터로 바꿔주지 않아도 자연스레 내적 연산을 진행합니다. 즉 원소 별 곱셈 연산 후 모든 요소를 더한 것과 같은 값이 나옵니다.

따라서 2차원 이하의 Array끼리의 연산에서는 차이가 없으나, 문제는 3차원 이상일 때부터 연산 결과가 달라질 수 있습니다.

이제 두 함수를 살펴볼 때, 아래의 예시를 참고해서 어떻게 연산방식이 다른지 살펴보려 합니다.

A = np.array([
        [[3, 1], 
        [3, 3]], 

        [[1, 1], 
        [3, 2]]])
B = np.array([
        [[3, 3],
        [3, 3]],

        [[1, 3],
        [2, 1]]])

이 때, A.shape, B.shape 모두 (2,2,2)임을 감안하고, 이들의 행렬곱 연산 시, 어떤 shape으로 나오는지도 주목해서 보면 도움이 될거 같습니다.

np.dot()

dot()은 A의 각각의 모든 행벡터와 B의 각각의 모든 열벡터끼리 내적 연산을 진행합니다.

아래 예시를 참고하면 각 행벡터에 4개의 열벡터가 각각 곱해져 2차원 배열을 생성하는 모습을 볼 수 있습니다.

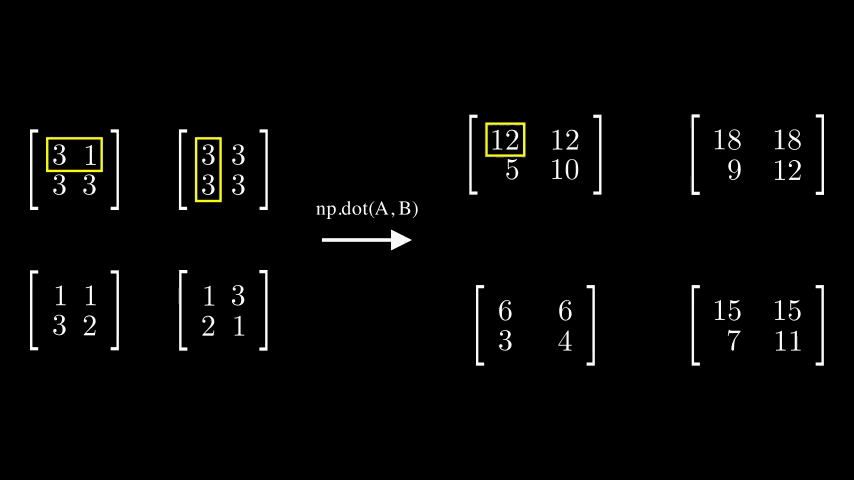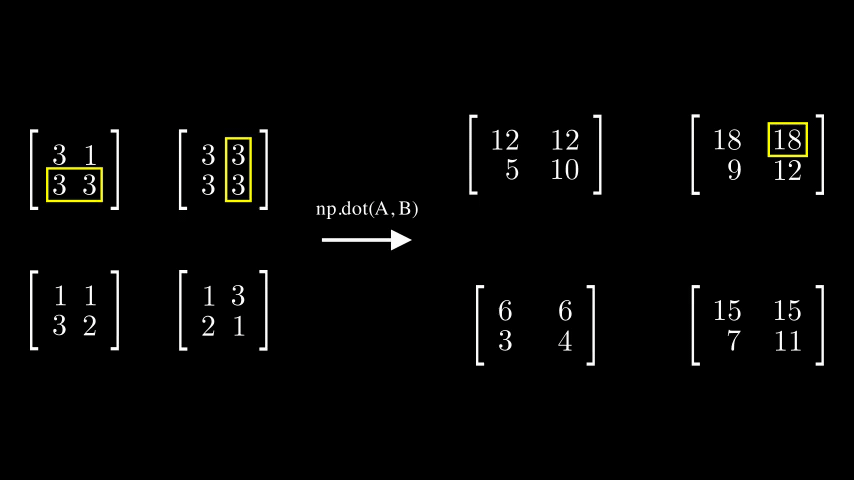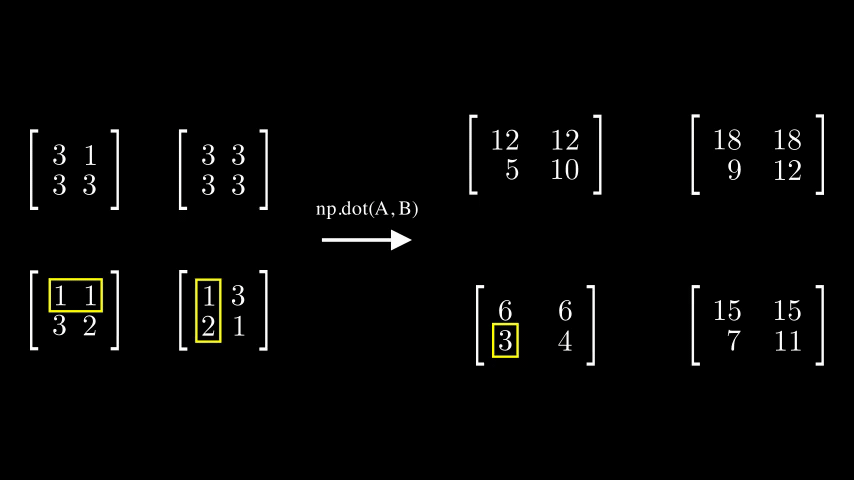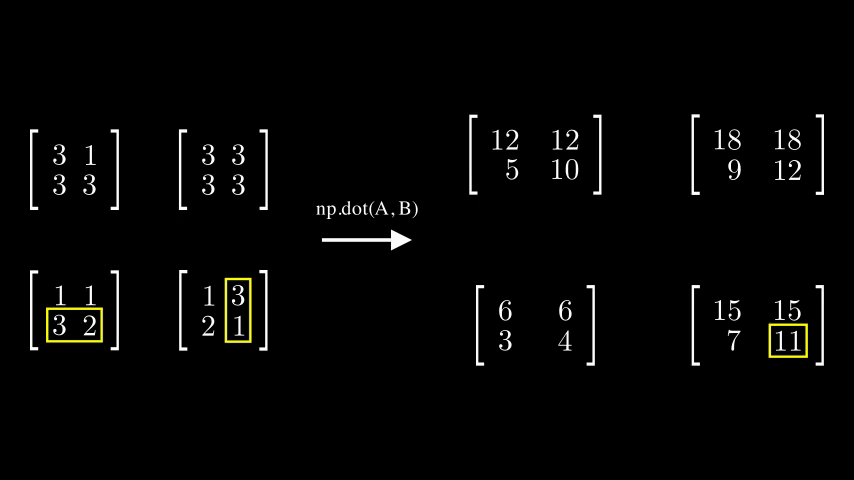이렇게되면 출력으로 나오는 Tenser의 shape는 어떻게 될까요?

하나의 2차원 배열에서 두개의 2차원배열이 들어가는 꼴이므로 차원이 하나 증가한, (2,2,2,2)shape의 Tensor가 나오는 것을 확인할 수 있었습니다.

np.matmul()

반면, matmul()은 각 텐서의 뒤에서 2개의 차원에 해당하는 행렬끼리 행렬곱 연산을 수행합니다.

예시에서는 뒤에서 2개의 차원에 해당하는 행렬은 A와 B 각각 $2\times 2$ matrix이며, 이 행렬끼리 연산하는게 어떤 모습인지 아래를 참고해보겠습니다.

즉, 첫번째 결과값으로 나온 2차원 행렬은 아래 연산을 수행되어 나온게 되겠군요.

이러한 행렬곱 연산이 2번 발생하니, (2,2,2)shape의 Tensor가 나오는 것을 확인할 수 있겠습니다.

---

그렇다면, 차원을 좀 더 높여서 두 함수의 출력 결과 차이를 알아볼까요?
이렇게 마무리하면 출력 결과를 매번 고민해야하니, 좀 더 정형화 해보도록 하겠습니다.

이제는 입력으로 들어오는 Tensor의 차원에서 뒤에서 두개의 차원에 둘 다 주목해서 보면 좋겠습니다.

아래 코드 예시를 보겠습니다.

import numpy as np

a = np.random.randn(5, 3, 16, 64)
b = np.random.randn(5, 3, 64, 8)


dot_result = np.dot(a,b)

matmul_result = np.matmul(a,b)

print(dot_result.shape)
print(matmul_result.shape)

(5, 3, 16, 5, 3, 8)
(5, 3, 16, 8)

우리가 행렬곱을 할 때 행렬곱이 가능한 경우와 그렇지 않은 경우가 있었습니다. 행렬곱은(n,k)*(k,m) = (n,m)일 때 결과가 나왔던 것처럼, k라는 부분이 같아줘야 합니다.

dot()은 앞 행렬의 모든 행벡터와 뒤 행렬의 모든 열벡터의 내적한 결과가 나오므로, 연산이 가능하려면 뒤에서 두개의 차원이 예시처럼 a : ( .., ..,16,64), b : ( .., ..,64,8) 이렇게 같아야 연산이 가능해집니다.
물론 이들이 다르면 오류가 발생하게 되겠죠.
따라서 출력 Tensor의 shape은 (5,3,16,64)$\cdot$(5,3,64,8) $\to$ (5,3,16,5,3,8)가 되겠습니다.

matmul()은 뒤에서 두개의 차원에 해당하는 행렬끼리 행렬곱이 진행되었으므로, 마찬가지로 뒤의 두개의 차원을 확인해줍니다.

이 때는 a : ( 5, 3, .., ..), b : ( 5, 3, .., ..)와 같이 앞의 두 차원이 크기가 같아야만합니다.
이로서 출력 Tensor의 shape은 앞부분은 같고 뒤에서 2개의 차원끼리 행렬곱 결과가 들어가 아래와 같은 결과를 얻을 수 있게 됩니다.

(5,3,16,64)$\cdot$(5,3,64,8) $\to$(5,3,16,8)

✍️차원 다루기

지난 포스팅에서 .arr[:,None], arr[:, np.newaxis]와 같이 차원축을 추가하는 방법을 알아봤었습니다. 참고로 둘 다 열에 차원축을 하나 추가한 연산이었는데요((3, ) $\to$(3,1)) 이번엔 차원의 축소에 대한 내용을 기록하였습니다.

차원 축소

사용 가능한 함수로는 np.squeeze(array,axis)와 np.reshape(array,size)가 있습니다. 만일 (4,2,1)shape의 Tensor를 어떻게 차원 축소할 수 있을지 알아보겠습니다.

## np.squeeze(array,axis)
import numpy as np

a = np.ones((4,2,1))
np.squeeze(a).shape
# np.squeeze(a, axis = 2)로 축을 지정할 수 도 있습니다.

(4, 2)

차원 축이 1인쪽이 자동으로 지워지며 차원 축소가 일어남을 알 수 있습니다.
이번엔 np.reshape(array,size)를 사용할 것인데, 여기서 -1을 사용하므로 나머지 부분은 알아서 채워지게됩니다.

np.reshape(a,(2,-1)).shape

(2, 4)

✍️Broadcasting

이 것에 대해서는 저번 TIL때 잠깐 다뤘었습니다. 잠깐 복습을 하면 아래의 내용이 있었는데요.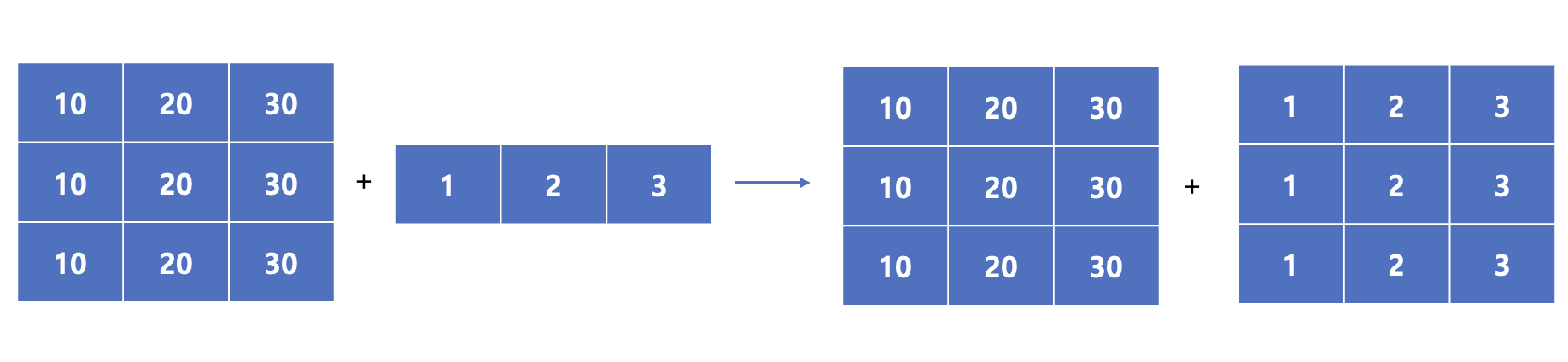shape이 (3,3)과 (1,3)인 array의 연산은 (1,3)$\to$(3,3)으로 Broadcasting되는 것을 살펴봤었습니다.

오늘 TIL에서는 이를 좀 더 정형화하여 2차원 이상에서는 어떻게 Broadcasting이 일어나는지 알아보고, matrix 또는 Tensor끼리의 연산에서 올바른 연산결과를 도출할 수 있는 능력을 갖춰보도록 하겠습니다.

$1.$ 같은 차원끼리 비교했을때 크기가 다르더라도 한 쪽차원의 크기가 1이면 브로드캐스팅이 가능하다

이는 위에서와 같은 상황을 말합니다. 이 말은 (2,3)$\to$(3,3)처럼 Broadcasting이 일어나지 않는다는 뜻입니다.

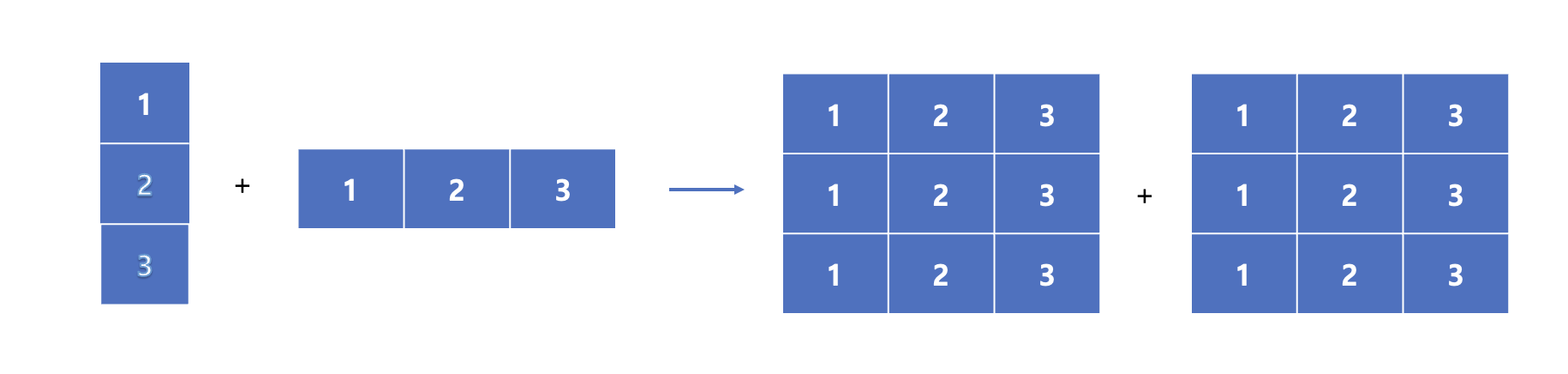
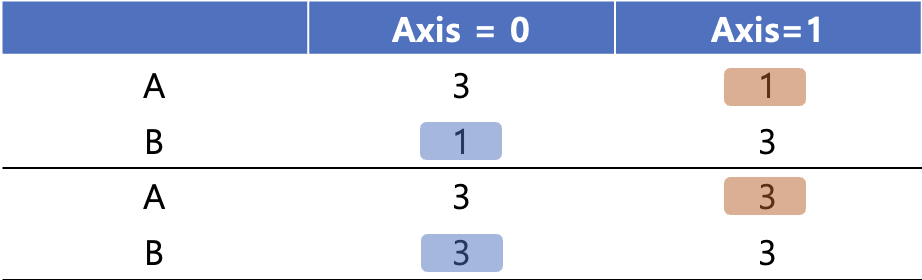
위와 같은 shape이 (3,1)과 (1,3) 연산에서는 1인쪽이 더 큰 3쪽으로 broadcasting되는 모습을 볼 수 있습니다. 따라서, 차원 크기가 다르더라도 1이라면 Broadcasting이 가능합니다!

$2.$ 차원의 레벨(array의 차원) 이 다르더라도 뒤에서부터 비교하여 크기가 같거나 차원의 크기가 1이면 브로드캐스팅이 가능하다

여기서부턴 3차원 이상의, Tensor-matrix나 Tensor-Tensor사이 Broadcasting에 대해 생각해볼 수 있습니다.

아래의 예시처럼 (2,1,3)과 (2,3)사이의 Tensor-matrix연산을 보겠습니다.

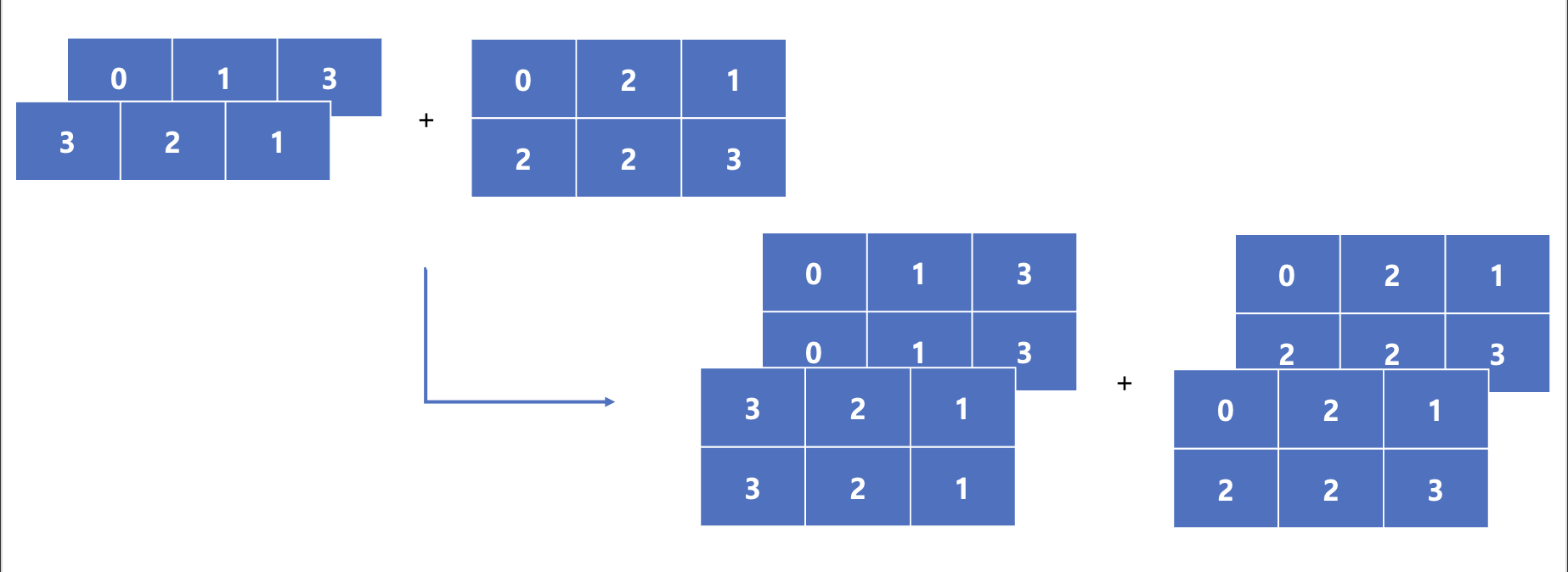
A는 3차원, B는 2차원의 Array입니다. 일단 차원이 안 맞지만 결론적으로 연산 수행은 가능합니다. 그럼 Broadcasting이 일어나는 과정을 살펴보겠습니다.

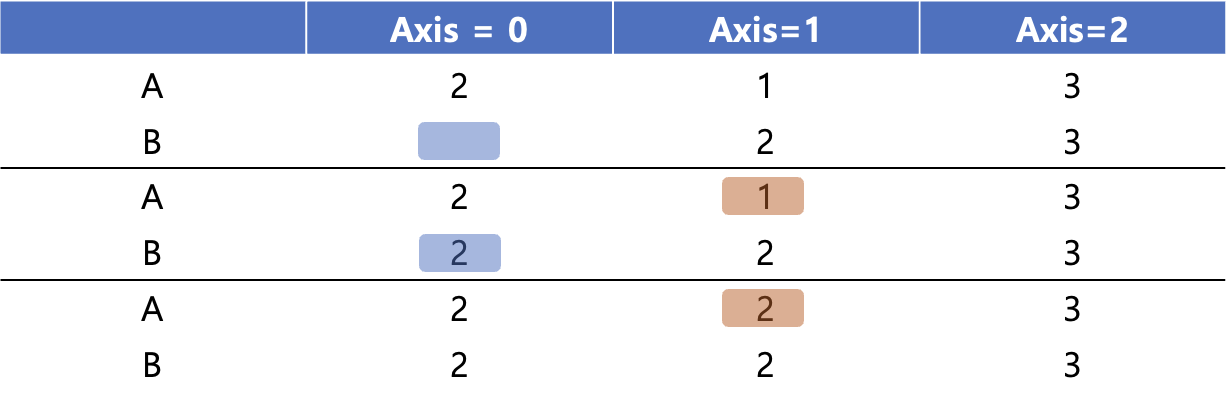
1️⃣ 최하위 차원부터 비교

위 그림처럼 작은 차원부터 비교하여 크기가 1인곳을 Broadcasting합니다. 이때 B의 3차원은 존재하지 않으나, 3차원 축 하나를 추가해서 기본적으로 크기를 1로 간주하여 차원크기를 맞추고, 이를 Broadcasting하는 모습을 볼 수 있습니다.

이해되셨다면 아래의 경우에 왜 연산 오류가 났는지 이해하실 수 있습니다.

a = np.ones((4,2,3))
b = np.ones((3,1))
(a+b).shape

---------------------------------------------------------------------------
ValueError                                Traceback (most recent call last)
Cell In[20], line 1
----> 1 np.squeeze(a, axis = 0).shape

File ~/opt/anaconda3/envs/DevCourse_6/lib/python3.10/site-packages/numpy/core/fromnumeric.py:1558, in squeeze(a, axis)
   1556     return squeeze()
   1557 else:
-> 1558     return squeeze(axis=axis)

ValueError: cannot select an axis to squeeze out which has size not equal to one

✍️ Bool indexing & Fancy indexing

조건식(&, |, ==, <=, ...)을 활용하여 np.array()에 대한 Bool array를 생성할 수 있는데요.
이 때 주의할 것은, python에서 사용할 때와 같이 and, or와 같은 식은 사용하면 적용되지 않는다는 것입니다.

A = np.array([1, 2, 3, 4, 5, 4, 3, 2, 1])
print(A >= 4 and A < 7) #print(4<= A < 7)도 마찬가지겠죠?

이런 오류를 만날 수 있습니다.

---------------------------------------------------------------------------
ValueError                                Traceback (most recent call last)
Cell In[27], line 2
      1 A = np.array([1, 2, 3, 4, 5, 4, 3, 2, 1])
----> 2 print(A >= 4 and A < 7)

ValueError: The truth value of an array with more than one element is ambiguous. Use a.any() or a.all()

이는 말그대로 python에서 사용한 구문일 뿐, Bool indexing을 활용하려면 조건식만을 활용해야 한다는 것을 기억해야하겠습니다.

Bool indexing에서는 조건식이 True가 나오는 index의 원소를 추출하여 원하는 값을 바로 빼낼 수 있습니다. 활용 예시의 첫번째를 아래와 같이 보겠습니다.

import numpy as np

np.random.seed(42)

arr = np.random.randint(0, 100, size=(5, 6, 3))

# arr에서 10보다 크고 20보다 작거나 같은 요소들만 추출해봅시다.
result =  arr[(10<arr) &(arr<=20)]
print(result)

또한 두번째 예시로 다음과 같은 문제를 만났을 때, bool indexing으로 쉽게 해결할 수 있었습니다.

---

---

import numpy as np

def solution(info): # bool index & fancy index
    return list(*np.where(~((150.0 <= info[0]) & (info[0] <= 195.0)) | ~(info[1,:] < 140.0)))

(array([1, 2, 4]),)
참고로 .where()은 인자로 받은 조건을 만족하는 index를 return합니다. return 형식이 (array([0, 1, ...], )와 같이 튜플 형식으로 나오게되어 *를 씌운 것입니다.

numpy에선 이처럼 array끼리 비교할 수 있는 연산이 다양하며 이를 Comperision이라고 합니다.

참고 : Comperision

arr_a = np.array([[1,3,5],[2,3,4]],float)
arr_b = np.array([[4,2,3],[7,5,1]],float)

# all과 any
arr_a < arr_b
'''output
array([[ True, False, False],
       [ True,  True, False]])
'''

np.all(arr_a<4) # 모두 True면 True를 return, 아니면 False
np.any(arr_a<4) # True가 존재하면 True, 아니면 False

(arr_a < arr_b).any()
'''output
True
'''

# and or not 로직을 활용할 수 있다.
np.logical_and(arr_a<3, arr_b >4)
np.logical_or(arr_a<3, arr_b == 4)
np.logical_not(arr_a<3, arr_b >4) # 둘중 하나만 True여도 True

# where
np.where(arr_a > 0 , 1, 0) # 조건이 참이면 1, 거짓이면 0을 반환하도록 return값을 설정해줄 수 있다.

np.where(arr_a>3) 
'''<output>
조건을 만족하는 index를 반환해준다. 0번 index는 axis 0, 1번 index는
axis 1을 뜻하여 각각 (0,2),(1,2)가 조건을 만족하는 index임을 return함.

(array([0, 1], dtype=int64), array([2, 2], dtype=int64)) 
'''

# argmax와 argmin : 최대 혹은 최소값을 가지는 원소의 index를 return 받는다.
np.argmax(arr_a) # arr_a가 1차원 배열일때 사용하자
np.argmin(arr_a,axis=0) # arr_a가 2차원 배열 이상일 때, axis를 이용하여 index를 return 받을 수 있다.
np.argsort(arr_a) # 오름차순으로 정렬했을 때 원소들에 대한 index를 배열로 return 받는다. axis로 기준을 설정할 수 있다.
np.argsort(arr_a)[::-1] # 내림차순 정렬

Fancy index

이는 어떤 한 Array의 원소들을 다른 Array의 index로 활용할 수 있음을 말합니다. arr_idx라는 0~9까지의 Array가 arr_t의 index 0~9까지를 불러 새로운 Array로 저장된 것을 볼 수 있습니다.

import numpy as np

arr_idx = np.arange(10)
arr_t = np.random.randint(0,int(1e5),20)
arr_t[arr_idx] #matrix형태도 가능하다

arr_t : array([81694, 21847, 83738, 27213, 16683, 93531,51862, 11253, 92162, 22290, 98428, 63187, 58111,19725, 23739, 98898, 41130, 82625, 42710, 18198])

arr_t[arr_idx] : array([81694, 21847, 83738, 27213, 16683, 93531, 51862, 11253, 92162,
       22290])