
📌 "부분적인 최적해가 전체적인 최적해가 되는 마법! 언제나 통하지는 않지만, 이런 방법이 통하는 문제들을 만나보세요."
출제빈도 : 낮음
평균점수 : 낮음
탐욕법(Greedy)이란?
현재 상황에서 지금 당장 좋은 것만 고르는 방법 (욕망의 항아리)
단순히 가장 좋아보이는 것을 반복적으로 선택해서 최적의 해를 구할 수 있는지 검토하는, 정당성 분석이 중요하다.
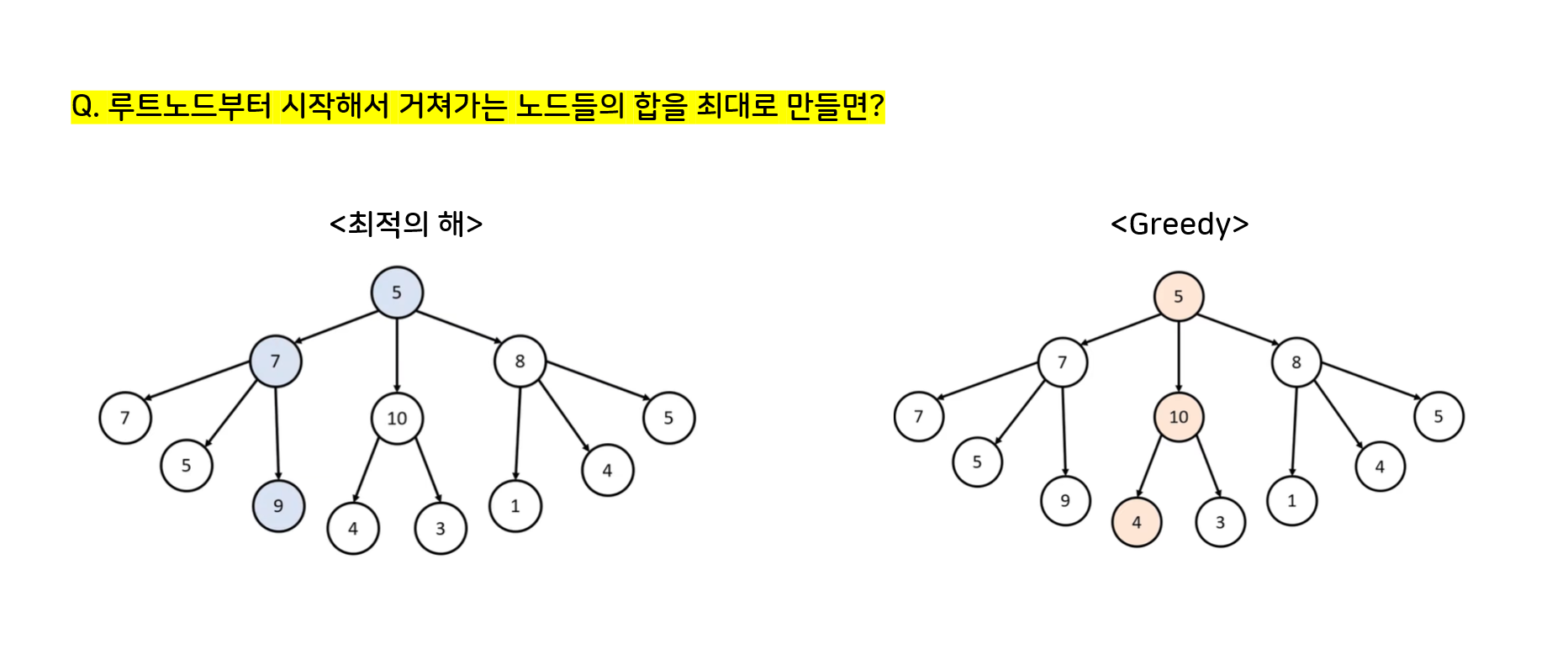
💡 탐욕법으로 풀리는 문제인지 추론하는 것이 포인트!
탐욕법을 적용하기 위해 성립해야할 조건
-
탐욕스러운 선택 조건 (Greedy Choice Property)
: 앞의 선택이 이후의 선택에 영향을 주지 않는다. -
최적 부분 구조 조건 (Optimal Substructure)
: 문제에 대한 최종 해결 방법은 부분 문제에 대한 최적 문제 해결 방법으로 구성된다.
이러한 조건이 성립하지 않는 경우에는 탐욕법으로 최적해를 구할 수 없지만, 이런 경우에도 어느 정도 최적에 근사한 값을 빠르게 도출할 수 있기 때문에 근사 알고리즘으로 사용할 수 있다.
cf) 탐욕법을 사용해서 언제나 최적해를 찾아낼 수 있는 특별한 구조를 '매트로이드'라고 한다.
- 주어진 상위의 값이 하위 값의 배수여야 한다.
대표적인 문제 1 : 거스름돈
Q. 거스름돈으로 사용할 500원, 100원, 50원, 10원짜리 동전이 무한히 존재한다. 손님에게 N원을 거슬러줘야 할때, 거슬러줄 동전의 최소 개수를 구하라.
🍄 가장 큰 화폐단위부터 돈을 거슬러주면 된다. 🍄
ex) N = 1260원 일때
남은 거스름돈 : 1260원
500원 => 2개
남은 거스름돈 : 260원
100원 => 2개
남은 거스름돈 : 60원
50원 => 1개
남은 거스름돈 : 10원
10원 => 1개
남은 거스름돈 : 0원가장 큰 화폐단위부터 거슬러주는게 최적의 해를 보장하는 이유는?
가지고 있는 동전 중에 큰 단위가 항상 작은 단위의 배수이므로, 작은 단위의 동전들을 조합해 다른 해가 나올 수 없기 때문이다.
예를들어 800원을 거슬러주어야 하는데, 화폐단위가 500원, 400원, 100원이라면 최적의 해는 400원 2개를 거슬러주는 것이지만, 그리디 방식이라면 500원 1개, 100원 3개, 총 동전 4개를 거슬러 줄 것이다.
다시 말해 100원 5개로 500원 1개를 만들 수 있는데, 문제에 따르면 이 경우에 100원 5개를 쓰는것보다 500원 1개 쓰는게 더 이득이기 때문에, 작은단위들을 모아 큰단위를 만드는 경우의 수를 애초부터 싹을 잘라버리고 큰단위로만 세는 것이다. 반면에 400원을 모아서는 500원을 만들 수 없기 때문에, 최적의 해가 나오지 않는 것이다.
n = 1260
count = 0
array = [500, 100, 50, 10]
for coin in array:
count += n//coin
n %= coin
print(count) # 6대표적인 문제 2 : 활동 선택 문제 (수업 시간표 짜기)
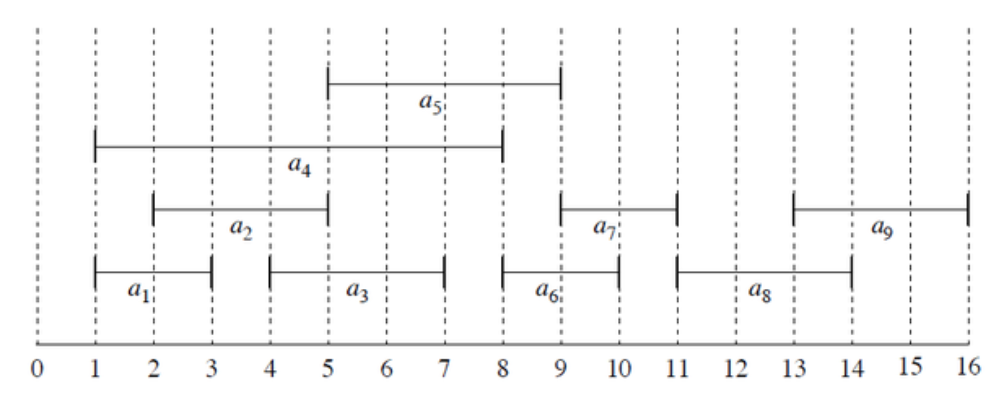
활동 N개의 시작시간과 종료시간이 주어졌을때, 최대한 많이 할 수 있는 활동의 수를 구하는 문제
- 가장 빨리 끝나는 활동을 고른다.
- 1에서 고른 활동이 끝난 후에 시작하는 활동 중 가장 빨리 끝나는 활동을 고른다.
- 시간표가 꽉 찰 때까지 1~2번을 반복한다.
다시말해, 종료시간을 기준으로 활동들을 정렬한 다음에, 현재 시점에서 선택할 수 있는 활동들 중 🍄가장 빨리 끝나는 활동🍄을 무조건적으로 선택하는 과정을 반복하면 된다.
N = int(input())
activity = []
for _ in range(N):
start, end = map(int, input().split())
activity.append((start, end))
activity = sorted(activity, key=lambda x:(x[1], x[0])) # 종료시간이 같으면 시작시간이 빠른 순으로 정렬
answer = 1
time = activity[0][1]
for start, end in activity[1:]:
if start >= time:
time = end
answer += 1
print(answer)ex) [1931] 회의실 배정
대표적인 문제 3 : 분할 가능 배낭 문제
코드
프로그래머스 고득점 Kit - 탐욕법(Greedy) 문제목록
1. 조이스틱 (Lv. 2)
74.1점짜리 내 코드 🤬
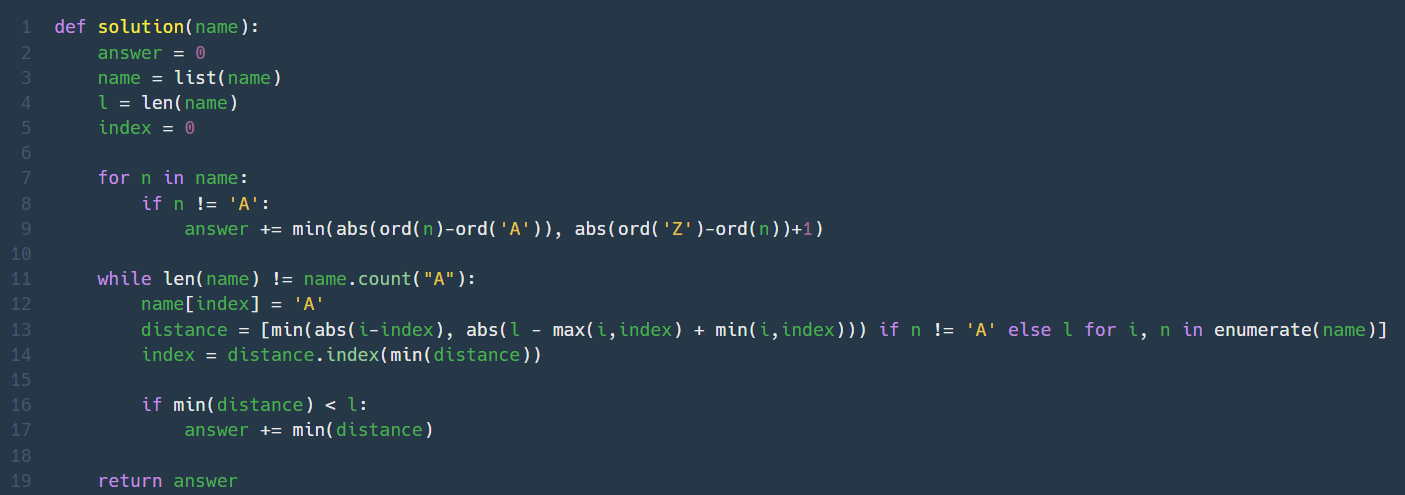
도저히 어느부분이 틀렸는지 하루종일 고민해도 모르겠어서 다른 사람 풀이를 봤다.
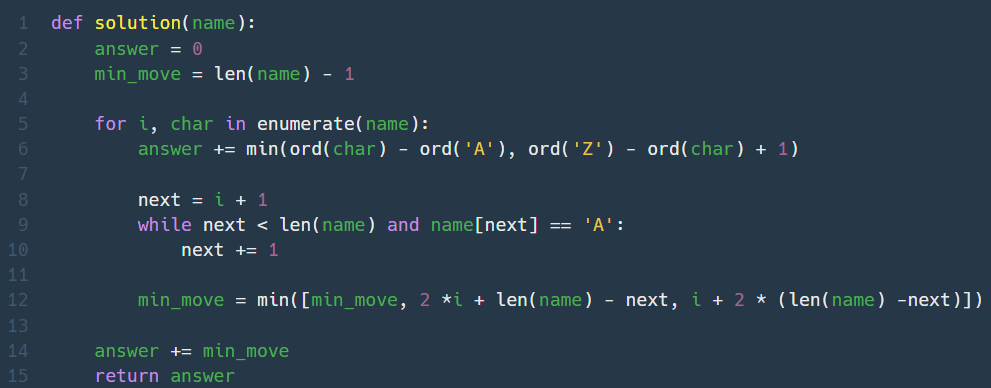
알파벳 변경 (상하) 조작 최소 횟수 = ord(바꿀문자) - ord('A'), ord('Z') - ord(바꿀문자) + 1 중 최소값
인건 맞았는데,
위치 변경 (좌우) 조작 최소 횟수 구하는게 틀렸다.
앞으로 이동해야하는 모든 위치에 대해 abs(다음위치-현재위치), abs(전체길이-현재/다음위치 중 큰 값+현재/다음위치 중 작은값) 중 더 작은 값을 넣은 리스트 중에 가장 작은값인 곳으로 이동하는 것으로 생각했는데, 아니랜다. 솔직히 아직도 이걸 뭐 어떻게 알아내서 풀라는건지 모르겠다. 짜증 만땅 후
🍄sum(지금 차례에 좌우로 움직일 수 있는 가장 적은 횟수 + 지금 차례에 상하로 움직일 수 있는 가장 적은 횟수)🍄
2. 큰 수 만들기 (Lv. 2)
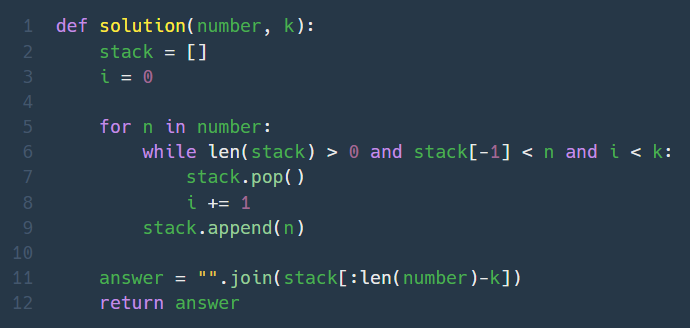
숫자를 앞에서부터 차례로 스택에 쌓는데, 스택의 top 이하에 지금 차례에 넣을 숫자보다 작은 숫자들이 있다면 모두 pop시킨다. (top부터 지금 넣을 숫자보다 크거나 같은 수가 나올때까지) k번 pop시키고 나면 남은 수가 작든 크든 쌓기만 한다. 스택에 쌓인 숫자들 중 전체길이-k번째 수까지가 답이다.
얘도 규칙을 도저히 모르겠어서 해법을 보고 풀었는데 어느 부분이 탐욕법인지 잘 이해가 안간다.
🍄누적된 숫자들 중 지금 넣는 수가 가장 크도록 숫자를 쌓는다. (누적된 숫자 중 지금보다 큰 건 내비둠)🍄
3. 구명보트 (Lv. 2)
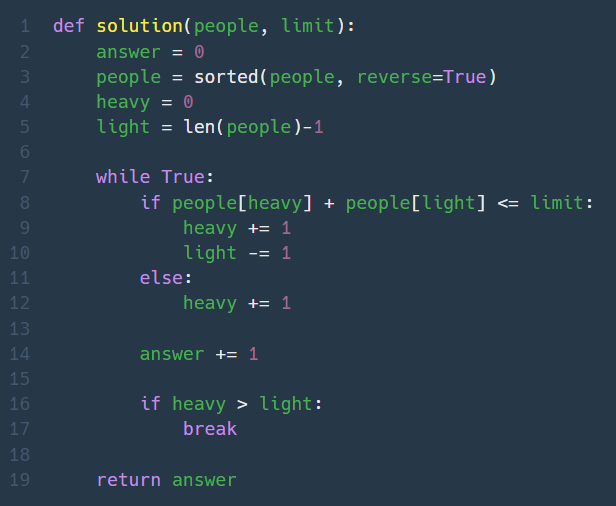
드디어 풀이 안보고 내 힘으로 풀어냈따....... ಥ_ಥ
무거운 순으로 정렬한 다음에, 지금 차례에 가장 무거운 사람과 가장 가벼운 사람의 무게 합이 limit 이하이면 같이 태우고, limit을 넘으면 무거운 사람만 태워서 보낸다. (가벼운 사람은 다음차례에 같이 태울 가능성이 있지만 무거운 사람은 무조건 혼자 타야하기 때문에)
🍄지금 차례에 가장 무거운 사람과 가장 가벼운 사람의 합이 무게 제한을 넘지 않으면 같이 태운다.🍄
4. 섬 연결하기 (Lv. 3)

얘도 풀이 안보고 성공! 아싸 ψ(`∇´)ψ
섬들을 하나씩 방문하면서, 건널 수 있는 다리들을 모두 모아놓은 다음에, 아직 방문하지 않은 섬으로 갈 수 있는 다리 중 가장 건설비용이 작은 다리를 선택해서 건넌다.
🍄아직 방문하지 않은 섬으로 갈 수 있는 다리 중 건설비용이 가장 작은 다리를 선택한다.🍄
5. 단속카메라 (Lv. 3)
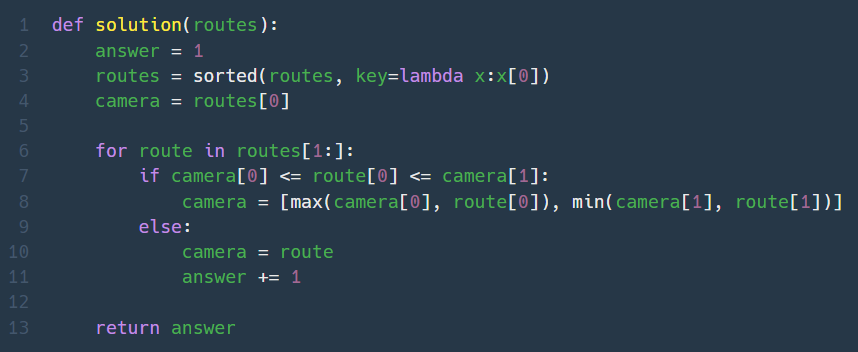
차량의 이동경로를 시작점이 작은것부터 오름차순으로 정렬한 다음, 순서대로 보면서 현재 차량의 이동경로가 이전에 책정된 카메라 설치 가능 구간 범위와 교집합이 형성되면 추가 설치 없이 카메라 설치 구간을 교집합 구간으로 업데이트하고, 교집합이 없으면 새로 카메라를 설치하는 것으로 보고 카메라 설치 구간을 현재 차량의 이동경로로 갱신한다.
🍄최대한 많은 차량이 공통적으로 지나는 구간에 카메라를 설치한다. 최대한 이번 차량도 지난번에 설치한 카메라에 걸리도록 한다.🍄
느낀점
- 🍄"지금 차례에 최대한 ~~한 선택을 하면, 이게 최종적으로도 가장 ~~한 답이 될 것이다"🍄가 중요한 포인트
- 무턱대고 풀기보다, 지금 어떤 선택을 해야 최종적으로도 최적의 해에 도달하는지 문제에 대해 정확히 분석하고 시작하는게 중요하다.
- 필요에 따라 "가장 ~~한 선택"을 하기 위해 스택이나 힙같은 자료구조를 적절히 사용할 것
