
대표적인 백트래킹 문제라는데.. DFS랑 뭐 다른가~ 하고 따로 정리 안하고 넘겼었는데 제대로 모르고 푸니까 헷갈림 두배 멍청함 세배라 이제라도 정리해보려고 한다.
백트래킹(Backtracking)
해를 찾는 도중 막히면 되돌아가서 다시 해를 찾는 기법

백트래킹으로 탐색하기 위해 DFS의 방식을 빌린다. (주로 재귀로 구현)
DFS와 백트래킹의 차이점
⭐ 차이점1.
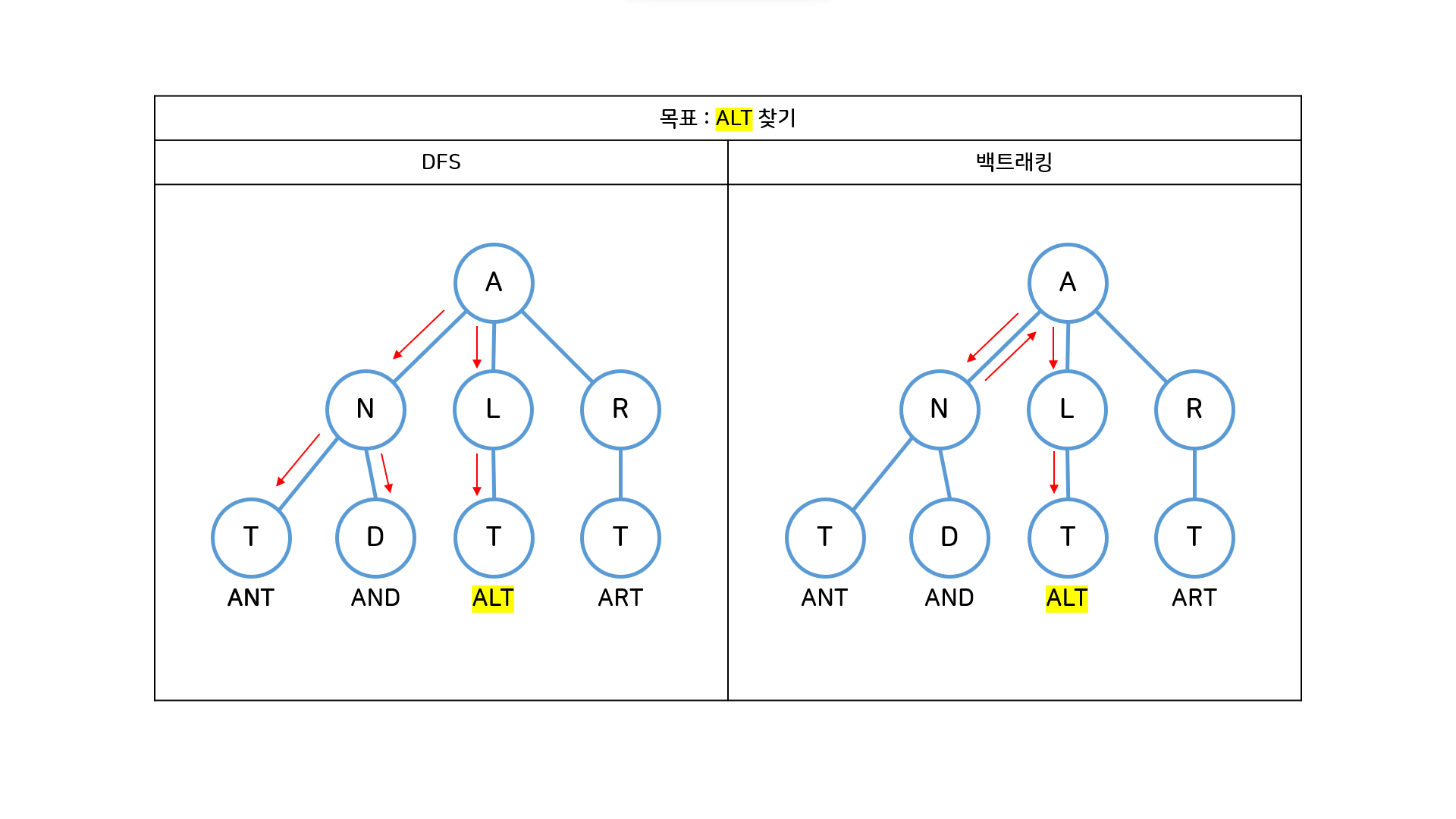
흔히들 DFS와 백트래킹의 차이점을 서술할 때 이렇게 말한다.
- DFS : 해를 찾을 때까지 가능한 모든 경로를 추적한다.
- 백트래킹 : 현재 방문한 노드가 해결책으로 이어질 것 같지 않으면 더 이상 해당 경로를 탐색하지 않고(가지치기) 되돌아와서 다음 경로를 탐색한다.
이것도 기본적으로 맞는 말이다. 근데 내가 더 찾아본 바로는 또 다른 큰 차이점이 하나 더 있다.
⭐⭐ 차이점2.
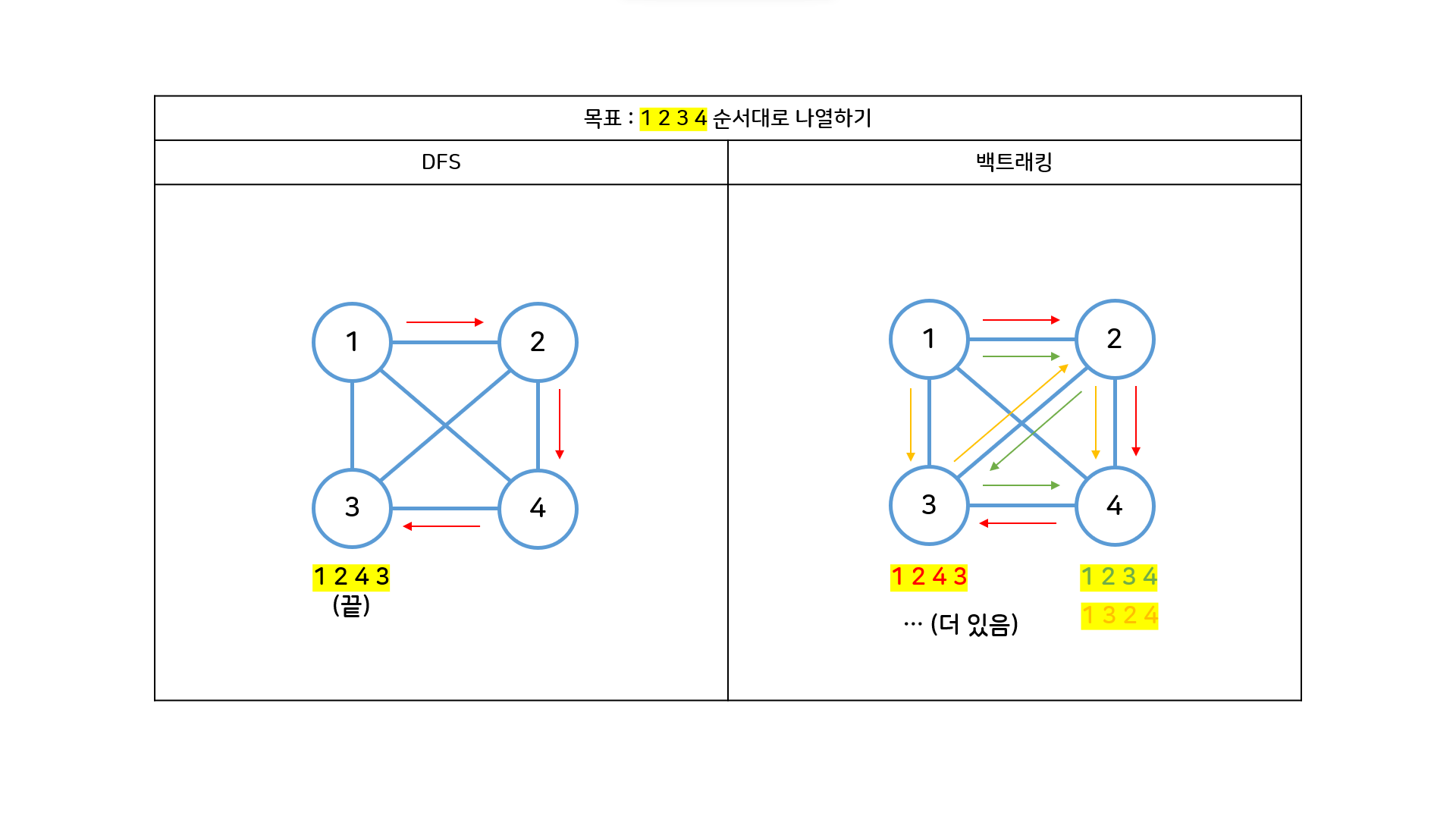
- DFS : 찾아야하는 경로가 여러 개일때, 모든 노드를 방문해서 경로 하나를 찾으면 다른 가능한 경로는 더 찾지 않고 종료한다.
- 백트래킹 : 찾아야하는 경로가 여러 개일때, 가능한 경로들을 모두 찾는다.
이번 차이점에서 알아낼 수 있는 중요한 포인트는, 백트래킹은 "같은 노드를 거치는 다른 경로들도 모두 찾아야 하기" 때문에, "이전에 방문한 노드를 다음 탐색에서 또 방문할 수 있다"는 점이다. 이를 위해서는 한 노드를 방문 처리하고 이후 탐색을 진행하고 돌아와서, 그 노드를 방문하지 않은 것으로 원상복구해야된다.
말로는 이해가 어려우니 예를 들어보자.
예시1. 순열
Q. 1, 2, 3, 4를 순서대로 늘어놓는 경우의 수를 구해보자.
1 2 □ □ 의 경우를 모두 파악했다면 다음에는 1 3 □ □ 을 채우기 위한 탐색이 진행될 것이다.
만약 DFS로 찾는다면?
=> 2는 이미 방문한 노드가 되어버리므로 1 3 □ □ 탐색 차례에서 2를 방문할 수 없게 된다.
만약 백트래킹이라면?
=> 1 2 □ □ 탐색이 끝난 후에 2는 다시 방문하지 않은 상태로 원상복구되기 때문에, 1 3 □ □ 탐색에서 2를 다시 방문할 수 있다.
예시2. 여행경로
이전에 풀었던 프로그래머스의 여행경로 문제도 사실 백트래킹이었다. (그땐 몰랐지만)
주어진 비행기 티켓들을 모두 사용해서 인천에서 떠나 다른 도시들을 거쳐 다시 인천으로 돌아오는 여행경로를 짜야하는데, 모든 가능한 여행경로를 찾으려면(ex. 인천->도쿄->뉴욕->인천 or 인천->뉴욕->도쿄->인천 등) 다음 경로 탐색을 위해 이번에 사용했던 티켓을 미사용으로 원상복구해야한다는게 이 문제에서 배운 점이었는데, 그게 백트래킹의 특징이었다.
표로 정리한 DFS와 백트래킹의 차이점

백트래킹의 기본코드
백트래킹의 기본틀은 아래와 같이 나타낼 수 있다.
def backtracking(n):
if 정답이면:
정답일때 수행할 일 (저장 or 출력)
return
else 정답이 아니면:
for 모든 자식노드에 대해서:
if 유망한지확인(m): # (1)
n 상태변화
backtracking(n+1)
n 원상복구 # (2)
def 유망한지확인(m):
if 조건에 안맞으면:
return False
return True설명을 조금 덧붙이자면
(1)에서 m이 유망한지 확인하고, 유망하지 않으면 더이상 탐색을 진행하지 않고 되돌아나가는 것이 바로 "백트래킹"이다. (첫번째 차이점)
(2)에서 다음 탐색을 위해 바꿔놓았던 상태를 원상복구시켜줘야 한다. (두번째 차이점)
여기서 상태변화<->원상복구 흐름이 헷갈려서 정리해보았다.
(1) visited를 원상복구하지 않았을 때
원상복구를 하지 않으면? (일반 DFS에서의 visited)
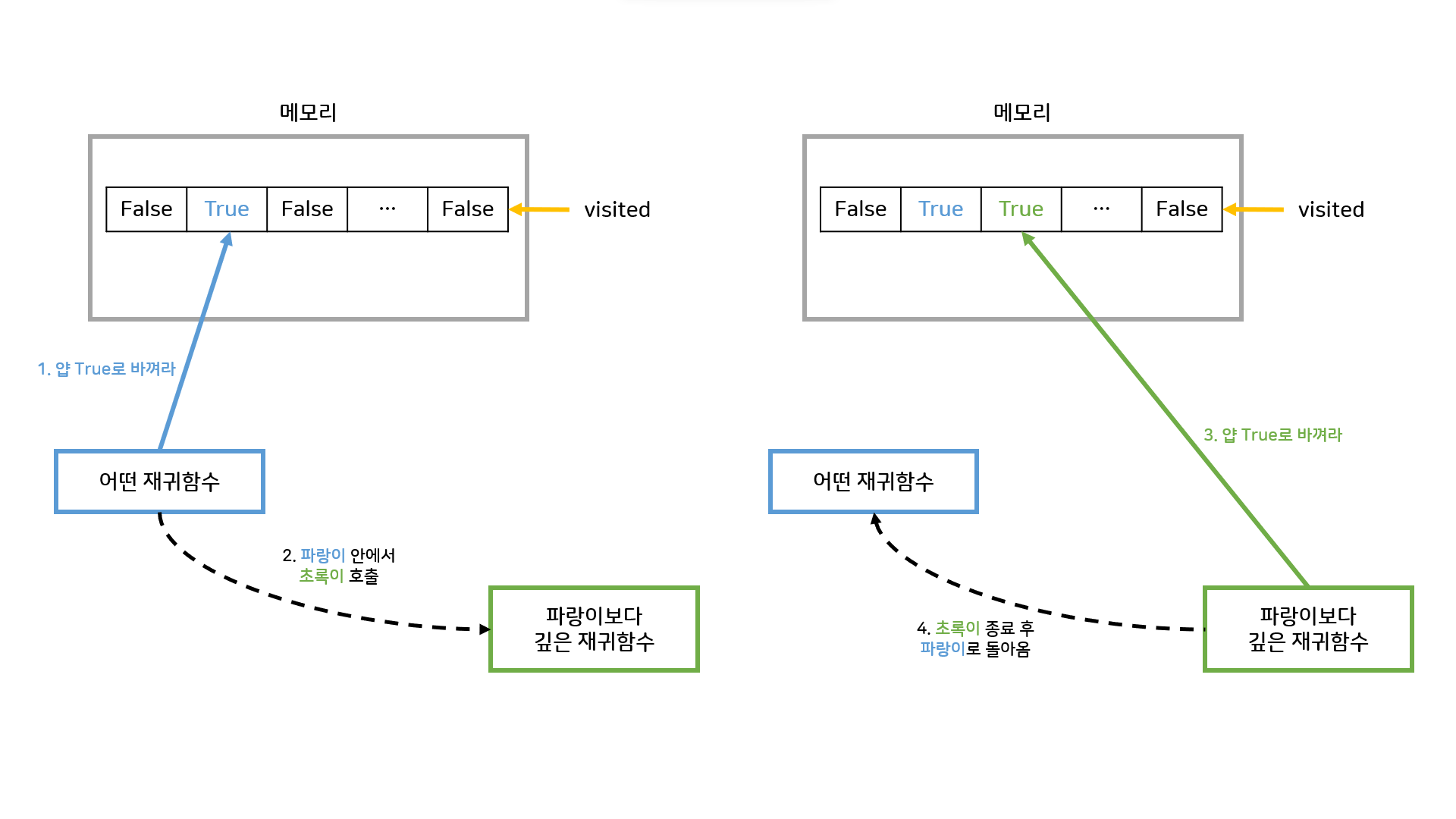

visited를 할당한 메모리 공간에 어떤 재귀함수를 타고 들어가서 값에 변화를 주면, 그 재귀가 끝났다고 할당한 값이 사라지는건 아니니까, 어찌보면 당연한 이야긴데 헷갈렸다. visited를 매개변수로 전달하든, 전역변수로 쓰든, 값이 변화되면 이후 과정 어디서든 똑같은 값을 가리키게 된다.
아무튼 일반적인 DFS는 다시 돌아왔을때, 한번이라도 방문한 노드는 이렇게 상태가 변화되어 다시는 방문하지 않는다.
(2) visited를 원상복구했을 때
그러나!! 백트래킹에서는 이미 방문한 노드를 다시 방문할 수 있어야 한다는 점!!
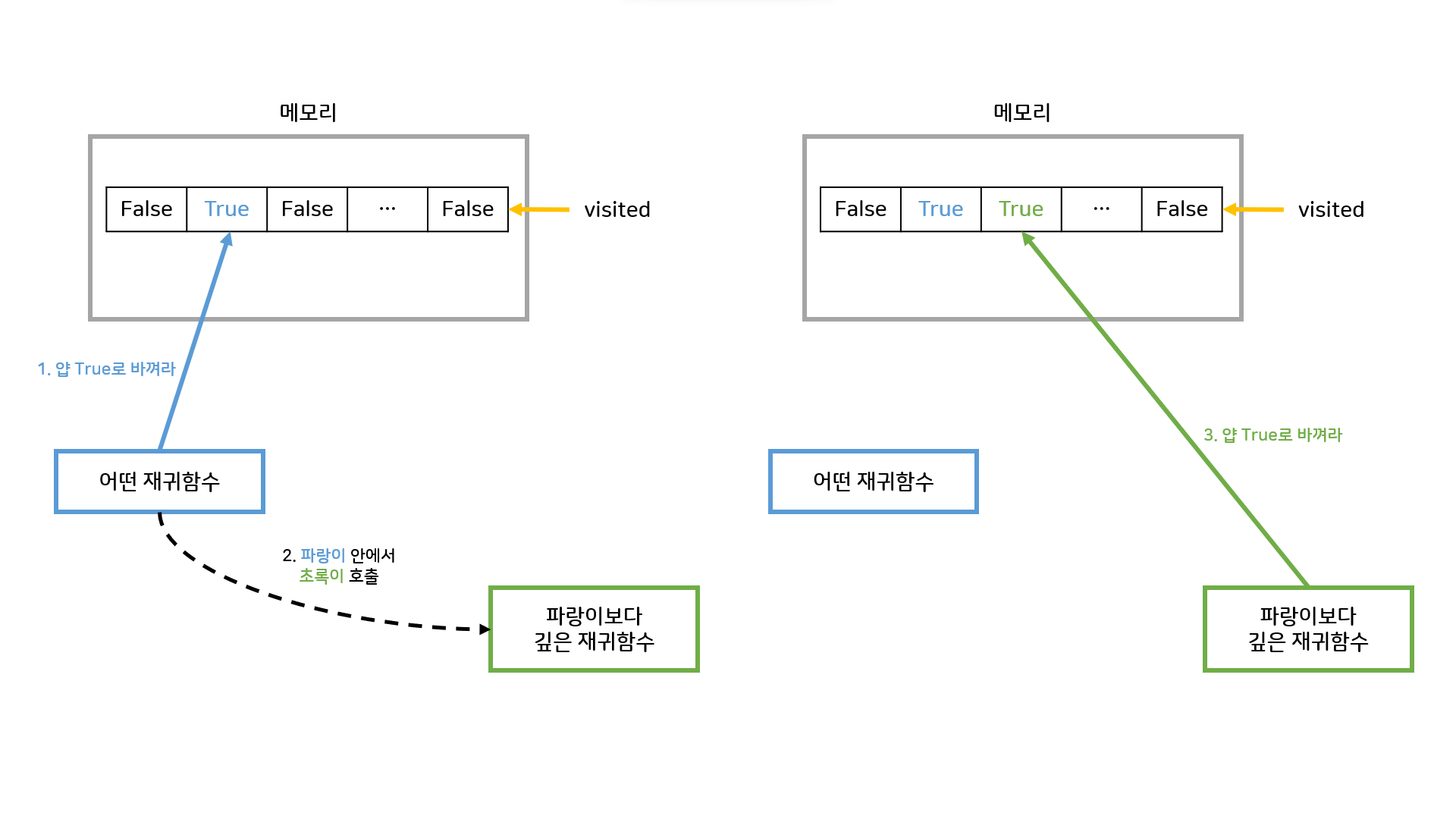
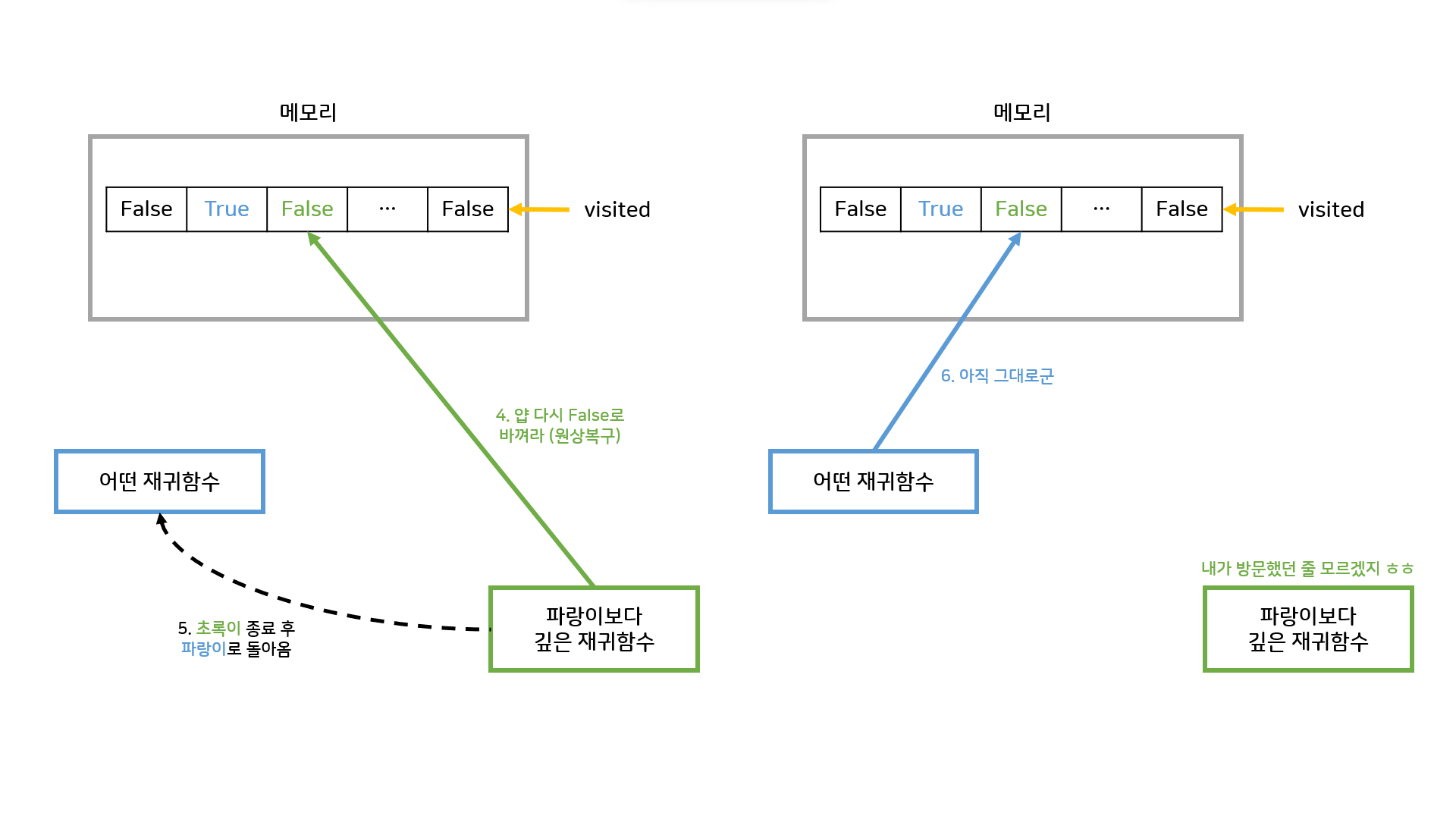
원상복구를 한다면? (백트래킹에서의 visited)
N-Queen 풀이 코드
그래서 내가 꾸역꾸역 짠 N-Queen 문제의 코드는 이렇다.
def backtracking(row): # row행에 놓는 경우
global N, board, cnt
if row == N: # 마지막행에 놓았으면
cnt += 1
return # 끝
else: # 중간행
for col in range(N): # 놓을 수 있는 모든 열에 대해서
if check(row, col): # row행 col열에 놓을 수 있다면 백트래킹 안하고 마저 진행
board[row] = col # row행 col열에 퀸 놓고
backtracking(row+1) # 다음행으로 이동
board[row] = -1 # 복구(사실 필요없는 과정)
# (생략) else: row행 col열에 놓을 수 없다면 더이상 진행X 되돌아감, 백트래킹
def check(row, col):
global board
for i in range(row): # row행 이전 행들만 봄 (이후는 아직 안놨으니까 볼 필요X)
if board[i] == col or abs(board[i]-col) == abs(i-row): # 이전행 같은열이나 대각선에 퀸이 이미 있을때는 불가능
return False
return True
N = int(input())
cnt = 0
board = [-1 for _ in range(N)] # board[row] = col : row행에는 col열에 놓음
backtracking(0) # 0행부터 놓기 시작
print(cnt)근데 python으로는 시간초과가 나서 pypy3으로 제출했다. (ㅎ)
📝 생각보다 너무너무 헷갈렸고 내가 막힌 부분에 대해 명쾌하게 이해가는 설명을 못찾아서 (특히 상태변화<->원상복구 부분) 내 나름대로 꾸역꾸역 이해한대로 썼는데 틀린 부분이 많을수도 있다..
➕ [1182] 부분수열의 합
(2023-08-30 추가)
1. 완전탐색
부분수열은 조합을 사용해서 구할 수 있다.
파이썬의 경우 itertools.combinations을 사용해 가능한 모든 부분집합을 구한 다음 합을 하나씩 다 구해볼 수 있다.
from itertools import combinations
nums = [전체 수열]
sums = [] # 부분수열들의 합
for i in range(1, len(nums)+1):
for c in combinations(nums, i):
sums.append(sum(c))2. 백트래킹
내가 직접 짠 코드는 너무 지저분해서 다른 사람 코드를 보고 다시 정리했다.
import sys
input = sys.stdin.readline
def subsequence(start):
global answer
if len(seq) > 0 and sum(seq) == S: # 부분수열의 길이가 0보다 크고 합이 S이면 정답
answer += 1
for i in range(start, N): # 내 다음 칸에 있는 숫자들이 곧 자식노드를 의미
# 모든 경우를 다 돌 것이므로 유망한지 확인하는 과정은 굳이 필요없다.
seq.append(numbers[i]) # 상태변화 (부분수열에 현재 숫자 추가)
subsequence(i+1) # 재귀로 다음탐색 진행
seq.pop() # 원상복구 (부분수열에서 현재 숫자 제거)
N, S = map(int, input().split())
numbers = list(map(int, input().split()))
answer = 0
seq = [] # 부분수열이 담기는 곳
subsequence(0) # 0번째 숫자부터 시작
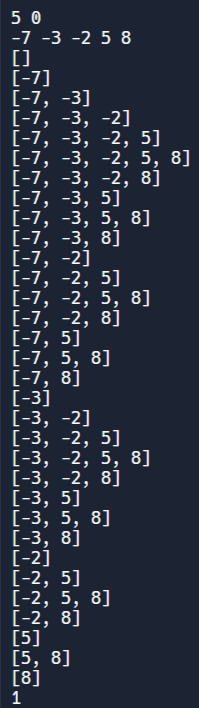
print(answer)부분수열이 만들어지는 순서

좋은 글 감사합니다 ! :>