OpenGL_07, Coordinate Systems

김경주·2024년 4월 17일
OpenGL
0

OpenGL

목록 보기
8/10

OpenGL은 모든 vertex들(vertices)이 각 vertex shade가 동작한 후 normalized device coordinate 안에 있길 예상한다. 이는 각 vertex의 x, y, z 좌표가 -1.0 ~ 1.0 사이에 있어야한다는 것. 이 범위 밖의 좌표들은 보이지 않는다. 보통 각자가 스스로 범위를 결정한 좌표계를 명시하고 vertex shader에서 이 좌표계를 NDC(normalized device cooordinate)로 변환한다. NDC는 스크린에 2D좌표,픽셀로 변환되기 위해서 rasterizer에게 주어진다.

좌표계를 NDC로 변환하는 것은 보통 최종적으로 물체들의 vertices들을 NDC로 변환되기 전에 그 vertices를 여러 좌표계로 변환하는 단계적 방식으로 하는 것. 좌표들을 여러 intermediate 좌표계들로 변환하는 이점은 몇가지 연산/계산들이 특정 좌표계에서는 더 쉬워진다는 것. 총 다섯가지 다른 좌표계들이 있다. 이는

  • Local space (or Object space)
  • World space
  • View space
  • Clip space
  • Screen space

여기 5가지 모두 다 다른 상태이며 vertices이 fragments로 되기전 변환되는 곳들이다.

The global picture

좌표들을 하나의 공간에서 다음 좌표 공간으로 변환하기 위해서 여러가지 변환 행렬을 사용할 것. 여기서 가장 중요한 것은 model, view, projection 행렬이다. vertex 좌표들이 제일 처음 지역(local) 좌표 또는 지역 공간에서 시작하고 그 후 world 좌표, view 좌표, clip 좌표 마지막으로 screen 좌표로 된다.

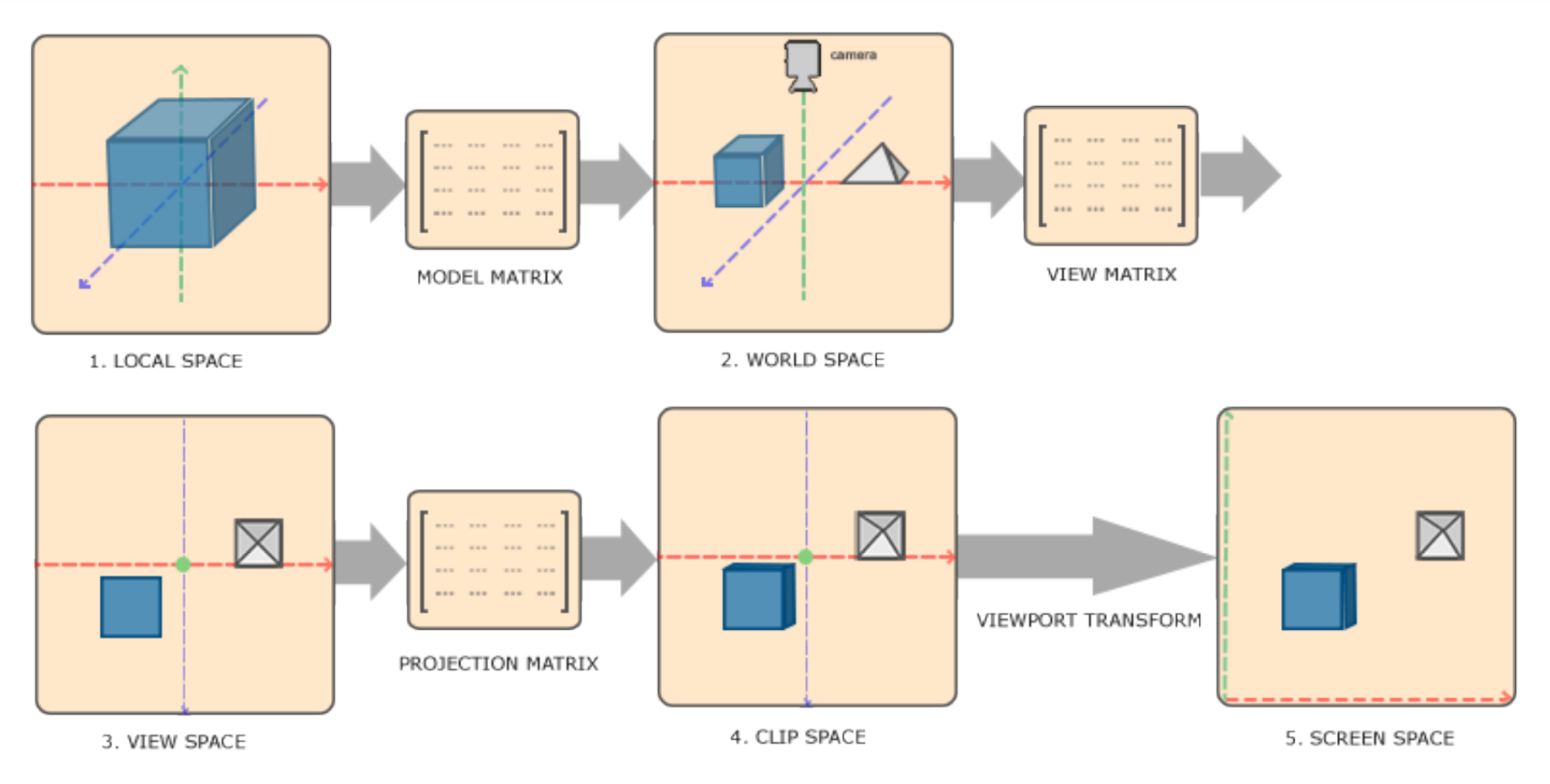
1. Local 좌표들은 local 원점과 연관있는 오브젝트의 좌표들, 오브젝트들이 시작하는 좌표.
2. 다음 단계는 local 좌표를 world-space 좌표로 변환(더 넓은 세계의 좌표). 다른 오브젝트들도 이 world의 기준으로 위치 조정
3. 그 다음 이 world 좌표들을 view-space로 변환 → 각각의 좌표는 카메라나 viewer의 시점인 방식
4. 이 후 view-space의 좌표들을 clip 좌표로 투영. Clip 좌표들은 -1.0 ~ 1.0 범위로 처리하며 어떤 vertices들이 스크린으로 나타나는지 결정. 이 clip 좌표들을 원근 투영을 원하면 원근법 추가할 수 있다.
5. 마지막으로 glViewport에 정해진 범위 -1.0 ~ 1.0으로 좌표들을 변환하는 viewport 변환을 호출하는 처리로 clip 좌표를 screen 좌표로 변환. 이 결과를 fragment들로 되게 하기 위해서 rasterizer로 전송.

각 공간에 어떤 것을 사용할지 알고 있을 것이다. 각각의 다른 공간들에 vertices를 변환하는 이유는 특정 좌표계에서 몇몇 연산들은 좀 더 타당하고 쉽게 사용할 수 있는 점이다. 예를들어 오브젝트를 수정할 때 local space에서 연산하는게 가장 알맞고 반면에 오브젝트들의 위치에 관해서 계산하는 특정 연산들은 world-space에서 가장 알맞는다. Local-space에서 clip-space까지 한번에 하나의 변환 행렬을 할 수도 있다. 다만 좀 더 낮은 유연성을 지닌다.

Local space

Local space는 오브젝트가 시작하는 오브젝트의 지역에 관한 좌표 공간이다. Blender 같은 모델링 소프트웨어 패키지에서 큐브를 생성한다고 생각해보자. 마지막 응용단계에서 큐브의 위치는 다를지라도 큐브의 원점은 (0, 0, 0)일 것이다. 아마도 생성한 모든 모델 오브젝트들은 (0, 0, 0)의 시작 지점을 갖는다. 따라서 모든 모델의 vertices들은 local-space에 있다.

World space

모든 오브젝트들을 애플리케이션에 바로 불러오면 (0, 0, 0)의 world 좌표계의 원점에 서로 겹쳐져 있을 것. 더 큰 세계 안에 각 오브젝트들의 위치를 정의해야한다. World space의 좌표는 말 그대로 world에 연관된 vertices의 좌표. 어떤 장소 주변에 각 오브젝트들이 흩어져 있는 방식으로 오브젝트들을 변환하는 좌표 공간이다. 이는 model 행렬로 수행한다.

Model matrix는 오브젝트들이 world에 놓여지는 위치와 방향에 맞게 이동, 크기 조정, 회전 변환을 하는 행렬.

View space

OpenGL의 카메라로서 보통 언급되는 것이 view space이다. 이는 camera space 또는 eye space라고도 한다. View space는 world-space의 좌표를 사용자 시점 앞으로의 좌표로 변환한 결과이다. 더구나 view-space는 카메라의 시점으로부터 보여지는 공간이다. 회전과 이동 조합의 변환으로 카메라 앞으로 특정 오브젝트들이 변환되게 수행된다. 이런 결합된 변환은 보통 view matrix 안에 저장되어있다.

Clip space

vertex shader의 동작 끝지점에 OpenGL은 좌표들이 특정 범위 안에 있는 것을 예상하며 범위를 벗어난 좌표들은 깎아내어진다(clipped). 깎여진 좌표들은 버려지고 남겨진 좌표들은 fragment로 되어 스크린에 보여진다.

보여지는 모든 좌표들을 -1.0 ~ 1.0 범위로 명시하는 것은 직관적이지 못하기 때문에 개별의 좌표계를 알맞게 설정하고 OpenGL이 알 수 있는 NDC로 변환한다.

vertex 좌표들을 view에서 clip space로 변환하기 위해서 좌표를 명시하는 projection matrix라 불리는 것을 정의한다. 예를들어 각 차원에서 -1000 ~ 1000인 좌표 범위. 그럼 projection matrix는 그 명시된 범위 안의 좌표들을 NDC(-1.0 ~ 1.0)으로 변환한다. 범위 밖의 좌표들은 -1.0 ~ 1.0 사이에서 맵핑되지 않고 짤리게 될 것. Projection matrix에서 명시된 좌표내에 좌표(1250, 500, 750)은 보여지지 않는다. 왜냐하면 x 좌표가 범위 밖이고 NDC로 변환되면 1.0보다 큰 값이기 때문이다. 그러므로 깎여진다.

Projection matrix가 생성하는 viewing box는 절두체(frustum)이라 불리고 이 frustum 내부에 속하는 각 좌표들은 스크린으로 보여진다. 명시된 범위 안의 좌표들을 2D view-space 좌표로 맵핑될 수 있는 NDC로 변환하는 총 과정을 projection이라 한다. 이 projection matrix는 3차원 좌표를 쉽게 2차원으로 맵핑하는 NDC로 투영하기 때문이다.

모든 vertices가 clip-space로 변환되었을때 마지막 연산인 perspective division이 작동하는데 이 작동하는 부분은 벡터의 동차좌표계의 원소 w에 의해 각 위치 x, y, z 요소가 나누어지는 곳이다. Perspective division은 4D clip space 좌표들을 3D NDC로 변환하는 것. 이 단계는 vertex shader 단계의 마지막 부분에 자동으로 수행된다.

이 단계 이후 결과로 나온 좌표들이 glViewport의 설정을 이용하여 스크린으로 맵핑되고 fragment로 된다.

view 좌표들을 clip 좌표로 변환하는 projection matrix는 보통 두 가지 다른 형식을 취한다. 각각의 형식은 특정 frustum을 정의한다. Orthographic(정사영) projection이나 perspective(원근) projection을 생성할 수 있다.

Orthographic projection

Orthographic projection matrix는 큐브와 같은 frustum box를 정의하는데 이 box는 이 box의 범위 밖의 각 vertex가 clipped(깎여진)된 곳인 clipping space를 정의한다. Orthographic projection matrix를 생성할 때 보이는 frustum의 길이, 폭, 높이를 명시한다. 이 frustum 안의 모든 좌표는 이 행렬의 변환 후 NDC 범위 안에 속할 것이고 clipped되지 않는다. 이 frustum은 컨테이너 같이 보여진다.

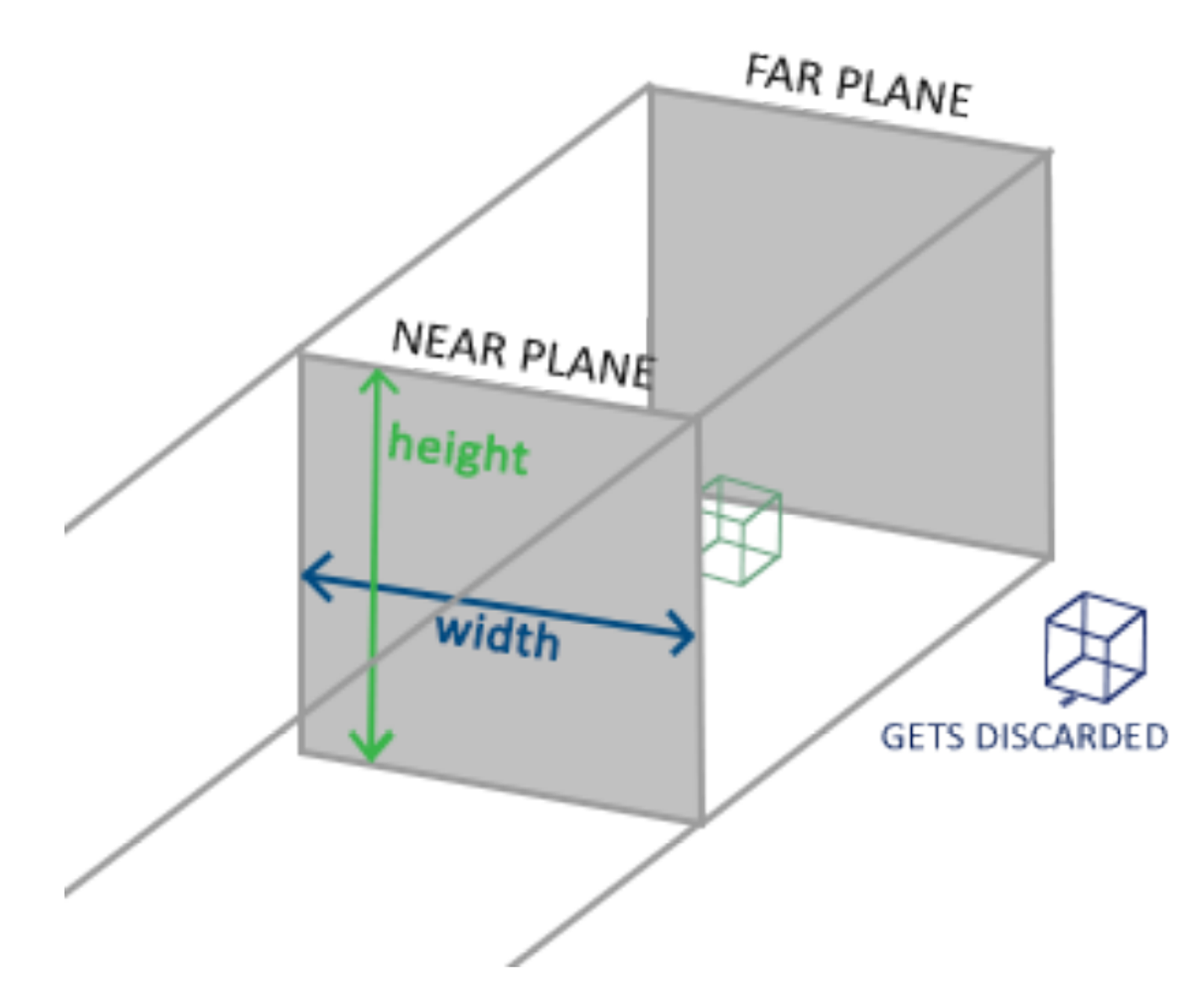
이 frustum은 보여지는 좌표들을 정의하며 폭, 높이, 가까운 평면(near plane)과 먼 평면(far plane)으로 명시된다. 가까운 평면 앞의 좌표와 먼 평면의 뒤 좌표는 clipped된다. 이 orthographic frustum은 frustum 내의 모든 좌표를 NDC로 바로 맵핑한다. 이는 부작용(side effects)가 없는데 왜냐하면 변환된 벡터의 w 요소를 건들지 않기 때문이다. 만약 w 요소의 값이 1.0이라면 perspective division은 좌표를 바꾸지 않는다.

이 정투영 행렬을 생성하기 위해서 GLM의 built-in 함수 glm::ortho를 사용한다.

glm::ortho(0.0f, 800.0f, 0.0f, 600.0f, 0.1f, 100.0f);

첫번째 두 인자는 frustum의 좌우 좌표를 명시하고 세번째 인자와 네번째 인자는 위아래의 좌표를 명시한다. 이 네 점들로 가까운 평면과 먼 평면의 크기를 정의했고 다섯번째와 여섯번째의 인자는 두 평면의 거리를 정의한다. 이 특정 projection 행렬은 정해진 x, y, z 범위 내의 모든 좌표를 NDC로 변환한다.

Orthographic projection matrix는 비현실적 결과를 낳는데 이는 원근감을 고려하지 않았기 때문이다.

Perspective projection


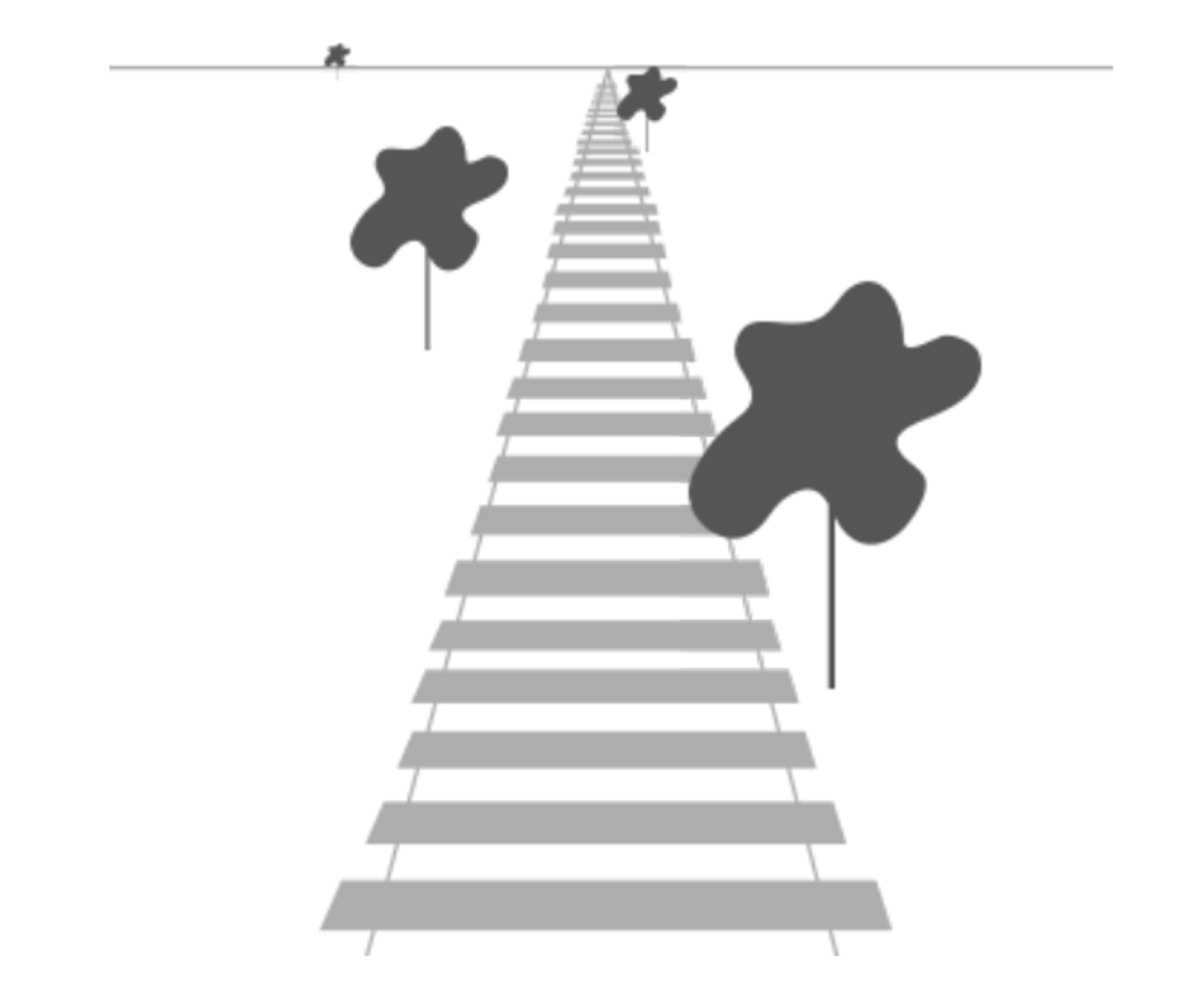
그림처럼 원근법으로 인해 거리에 따라 차이가 보인다. Perspective projection matrix를 사용하여 이러한 효과를 모방한다. Projection matrix는 clip space에 주어진 frustum 범위에 매핑될 뿐만아니라 viewer로부터 거리가 멀수록 w 요소의 값은 더 올라가는 방식으로 각 vertex 좌표의 w 값을 조작한다. 좌표들이 clip-space로 변환되었을 때 좌표들은 -w ~ w 범위 안에 있다(범위 밖은 clipped). OpenGL은 보여지는 좌표들이 최종 vertex shader 출력값으로 -1.0 ~ 1.0 범위로 떨어지는 것을 요구한다. 이렇게하여 좌표들이 clip-space에 있을 때 perspective division은 clip-space 좌표들에 적용된다:

out=(x/wy/wz/w)out = \begin{pmatrix}x/w\\y/w\\z/w\end{pmatrix}

vertex 좌표의 각 요소는 w 요소로 나누어진다. 이는 w요소가 왜 중요한지 말해준다. 결과로 나온 좌표들은 이제 NDS에 들어간다.

참고자료 시작

Projection matrix(https://www.songho.ca/opengl/gl_projectionmatrix.html)

컴퓨터 모니터는 2D 표면, OpenGL에 의해 렌더링되는 3D 장면들은 2D 이미지로 스크린에 투영되어야한다. GL_PROJECTION 행렬은 이 projection 변환을 위해 사용된다. 첫번째 이것은 모든 vertex 데이터들을 view space 좌표에서 clip space 좌표로 변환한다. 이후 이 clip 좌표들은 clip 좌표 w 요소로 나누어지는 것에 의해 NDC로 변환된다. 그러므로 clipping과 NDC 변환은 GL_PROJECTION으로 통합되어 있다. 6개의 파라미터(left, right, bottom, top, near and far)로 projection 행렬을 만드는지 알아보자

clipping은 clip 좌표들로 수행되는데 이는 wcw_c요소로 나누기 바로 전이다. clip 좌표 xcx_c, ycy_c, zcz_c는 wcw_c와 비교하여 검사된다. 만약 셋 중 어느 좌표가 −wc-w_c보다 작으거나 wcw_c보다 크면 그 vertex는 버려진다.

−wc<xc, yc, zc<wc-w_c < x_c,\,y_c,\,z_c < w_c

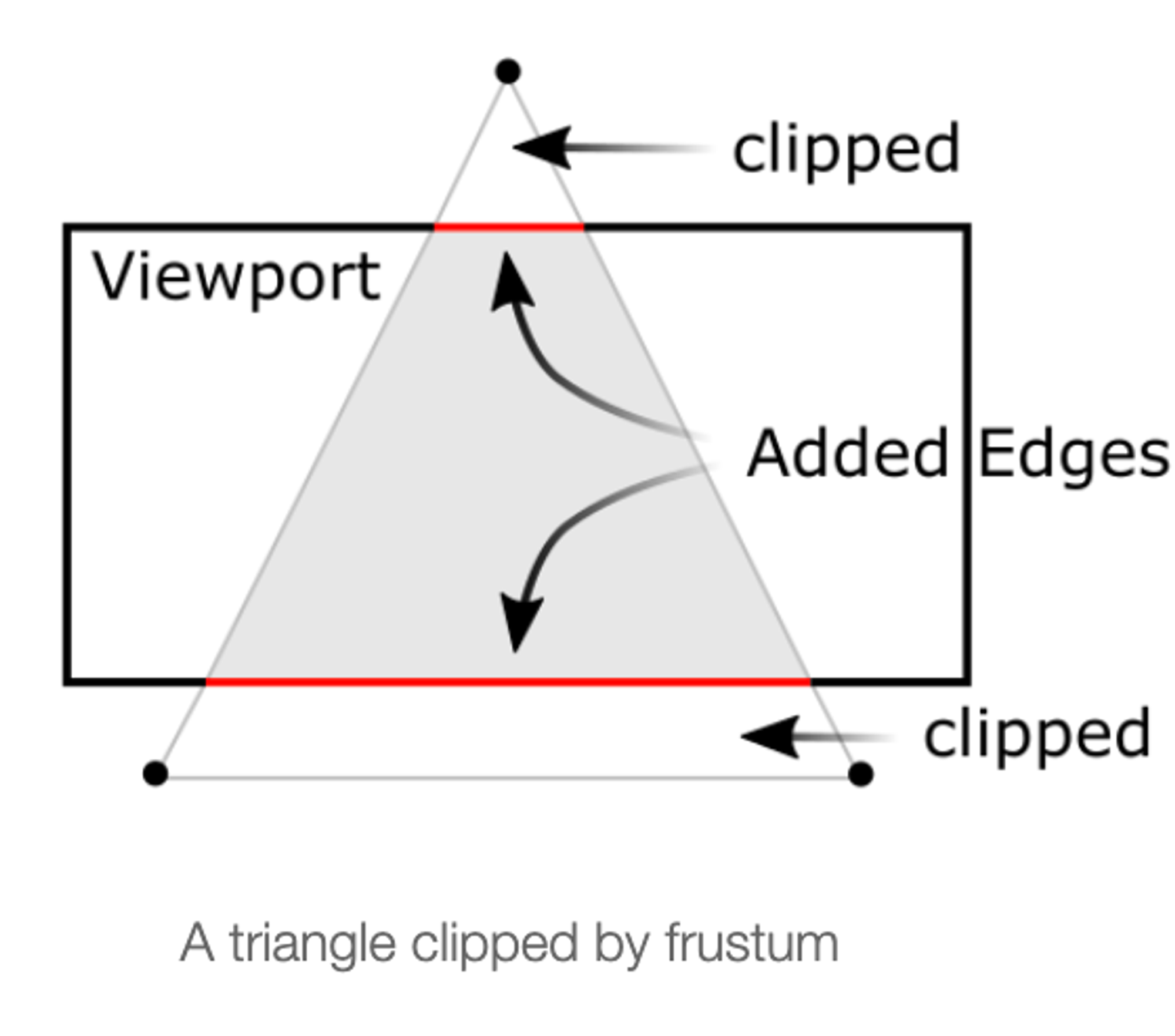
그 이후 OpenGL은 clip이 발생한 다각형의 끝지점들을 재구성한다.

Perspective Projection

perspective projection에서 끝이 짤린 피라미드형의 절두체에서 3D point(view 좌표)는 큐브(NDC)에 매핑된다.

x 좌표의 범위는 [l, r] → [-1, 1], y 좌표의 범위는 [b, t] → [-1, 1], z 좌표의 범위는 [-n, -f] → [-1, 1]

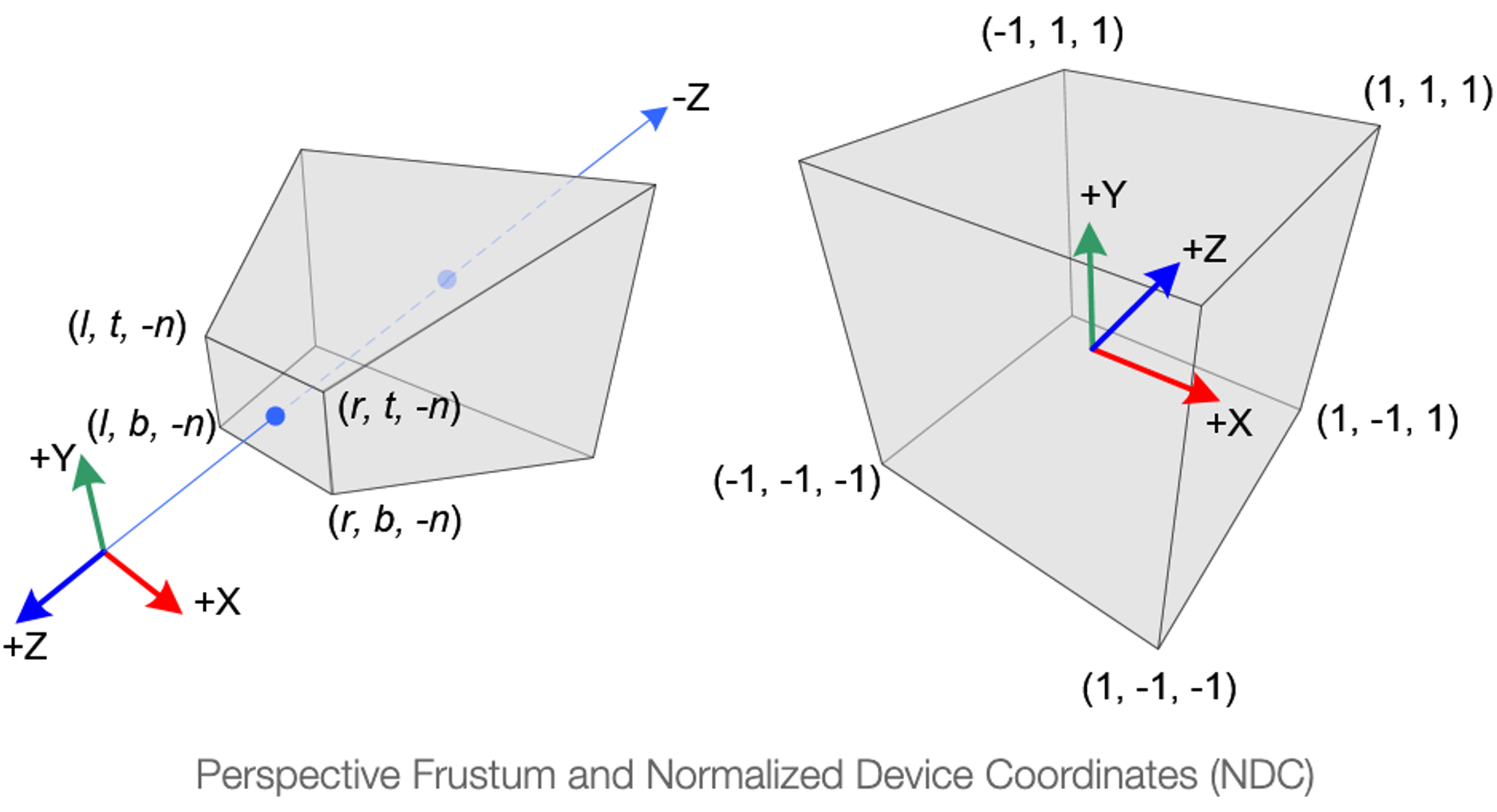
view 좌표는 오른손 좌표계, NDC는 왼손 좌표계. 이는 view space에서 원점에서 카메라는 -Z 축을 따라 보고 NDC에서는 +Z 축을 따라 본다. glFrustum 함수는 near와 far의 거리의 값을 양수값만 취하기 때문에 GL_PROJECTION 행렬의 구성 중에 이들 값에 부호를 반대로 해야한다.

OpenGL에서 view space에서 3D point는 near 평면에 투영된 것.

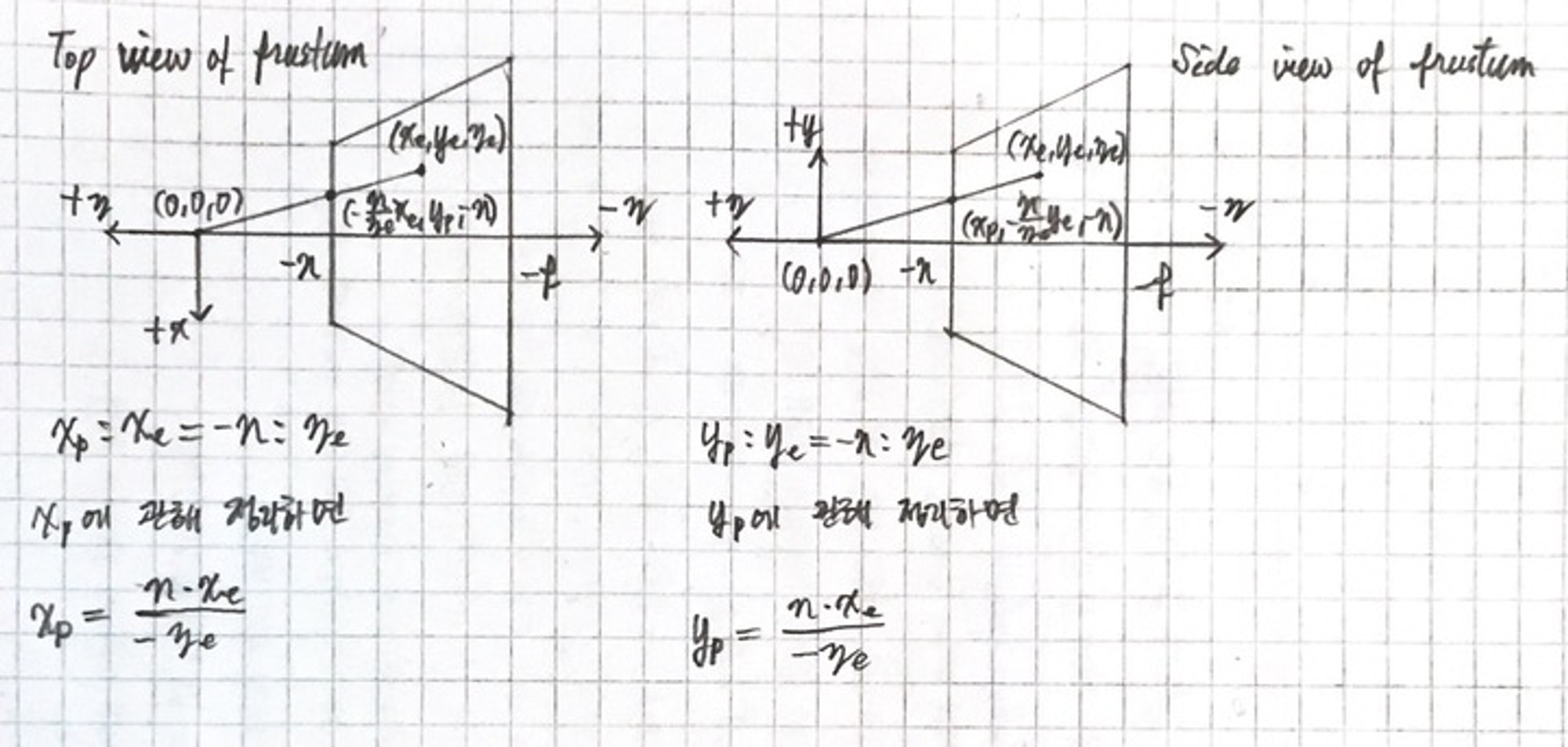
절두체의 상면도에서 view space의 xx 좌표 xex_e는 xpx_p와 매핑된다. 측면도에서 view space의 yy 좌표 yey_e는 ypy_p와 매핑된다. 여기서 xpx_p와 ypy_p는 zez_e에 종속된다. 이 두 좌표는 zez_e에 반비례. 이는 두 좌표가 −ze-z_e로 나누어진다는 말. GL_PROJECTION을 구성하는 첫번째 단서. GL_PROJECTION 행렬 곱에 의해 view space 좌표가 변환된 후에 clip-space 좌표들은 여전히 동차좌표계이다. 마지막으로 clip 좌표들의 ww 요소로 나누어짐으로 의해 NDC가 된다.

[xclipyclipzclipwclip]=MProjection⋅[xviewyviewzviewwview]\begin{bmatrix}x_{clip}\\y_{clip}\\z_{clip}\\w_{clip}\end{bmatrix} = M_{Projection} \cdot \begin{bmatrix}x_{view}\\y_{view}\\z_{view}\\w_{view}\end{bmatrix}, [xndcyndczndc]=[xclip/wclipyclip/wclipzclip/wclip]\begin{bmatrix}x_{ndc}\\y_{ndc}\\z_{ndc}\end{bmatrix}=\begin{bmatrix}x_{clip}/w_{clip}\\y_{clip}/w_{clip}\\z_{clip}/w_{clip}\end{bmatrix}

따라서 clip 좌표 ww 요소를 −ze-z_e로 설정

[xclipyclipzclipwclip]=[............00−10]⋅[xviewyviewzviewwview]\begin{bmatrix}x_{clip}\\y_{clip}\\z_{clip}\\w_{clip}\end{bmatrix} = \begin{bmatrix}\quad.\quad\quad . \quad\quad . \quad\quad .\quad\\.\quad\quad . \quad\quad . \quad\quad .\\.\quad\quad . \quad\quad . \quad\quad .\\ \quad 0\quad\quad 0\quad -1\quad\quad 0\quad\end{bmatrix} \cdot \begin{bmatrix}x_{view}\\y_{view}\\z_{view}\\w_{view}\end{bmatrix}

GL_PROJECTION 행렬의 네번째 행의 요소들은 0, 0, -1, 0이며 wview=−zew_{view} = -z_e 이다.

다음은 xpx_p와 ypy_p를 NDC의 xnx_n과 yny_n으로 일차 관계식으로 매핑하는 것.

그다음 위 방정식에서 xpx_p와 ypy_p에 그 위에서 구했던 값을 대입한다.

각 방정식에서 두 항 모두 xc/wcx_c/w_c, yc/wcy_c/w_c 에 맞게 −ze-z_e로 나누어지게 만들었다. 이로부터 GL_PROJECTION 행렬의 첫번째와 두번째 행을 만든다.

[xclipyclipzclipwclip]=[ 2nr−l0r+lr−l0  02nt−bt+bt−b0 ....00−10]⋅[xviewyviewzviewwview]\begin{bmatrix}x_{clip}\\y_{clip}\\z_{clip}\\w_{clip}\end{bmatrix} = \begin{bmatrix}\ \frac{2n}{r-l}\quad 0\quad \frac{r+l}{r-l} \quad 0\ \\ \ 0\quad\frac{2n}{t-b}\quad \frac{t+b}{t-b}\quad 0\ \\.\quad . \quad . \quad .\\ 0\quad 0\quad -1\quad 0\end{bmatrix} \cdot \begin{bmatrix}x_{view}\\y_{view}\\z_{view}\\w_{view}\end{bmatrix}

이제 세번째 행만 남았다. znz_n을 찾는 것은 이전 것들과 조금 다른데 왜냐하면 view space에서 zez_e는 항상 near 평면의 -n에 투영되기 때문이다. 그래서 clipping과 깊이 테스트에 관한 zz 값이 필요하다. 더해서 이에 대한 역변환도 가능해야한다. zz값이 xx와 yy에 종속되지 않기 때문에 zez_e와 znz_n 사이의 관계를 찾기 위해서 ww 요소를 빌린다. 따라서 세번째 행은 아래와 같다.

[xclipyclipzclipwclip]=[ 2nr−l0r+lr−l0  02nt−bt+bt−b0  0 0 A B00−10]⋅[xviewyviewzviewwview]\begin{bmatrix}x_{clip}\\y_{clip}\\z_{clip}\\w_{clip}\end{bmatrix} = \begin{bmatrix}\ \frac{2n}{r-l}\quad 0\quad \frac{r+l}{r-l} \quad 0\ \\ \ 0\quad\frac{2n}{t-b}\quad \frac{t+b}{t-b}\quad 0\ \\ \ 0\quad \ 0 \quad \ A \quad \ B\\ 0\quad 0\quad -1\quad 0\end{bmatrix} \cdot \begin{bmatrix}x_{view}\\y_{view}\\z_{view}\\w_{view}\end{bmatrix}, zn=zc/wc=Aze+Bwe−zez_n = z_c / w_c = \frac{Az_e + Bw_e}{-z_e}

view-space에서 w_e는 1이므로 방정식은

zn=zc/wc=Aze+B−zez_n = z_c / w_c = \frac{Az_e + B}{-z_e}이 된다.

A, B, 계수를 찾기 위해서 (znz_n, zez_e) 관계식을 사용. (-n, 1) 과 (-f, 1) 그리고 이것들을 위 방정식에 대입하면

GL_PROJECTION 행렬의 모든 요소를 찾았다. Projection 행렬은 아래와 같다.

[2nr−l0r+lr−l002nt−bt+bt−b0 00 −(f+n)f−n −2fnf−n00−10]\begin{bmatrix}\frac{2n}{r-l}\quad 0\quad \frac{r+l}{r-l} \quad 0\\ 0\quad\frac{2n}{t-b}\quad \frac{t+b}{t-b}\quad 0\ \\ 0\quad0 \ \frac{-(f+n)}{f-n}\ \frac{-2fn}{f-n}\\ 0\quad 0\quad -1\quad 0\end{bmatrix}

이는 일반적인 frustum에 관한 projection 행렬이다. viewing volume이 대칭적이라면 r=−lr = -l 과 같고 t=−bt = -b 이므로

[nr0000nt00 00 −(f+n)f−n −2fnf−n00−10]\begin{bmatrix}\frac{n}{r}\quad 0\quad 0 \quad 0\\ 0\quad\frac{n}{t}\quad 0\quad 0\ \\ 0\quad0 \ \frac{-(f+n)}{f-n}\ \frac{-2fn}{f-n}\\ 0\quad 0\quad -1\quad 0\end{bmatrix}

여기서 zez_e와 znz_n 사이의 관계식을 보면 유리 함수이면 비선형 관계이다. 이는 near 평명에 매우 높은 정밀도가 있고 far 평면에서는 매우 낮은 정밀도가 있음을 의미한다. 만약 [-n, f]의 범위가 커지면 커질수록 깊이 정밀도 문제(depth precision problem)을 야기시킨다. far 평면에서의 zez_e의 작은 변화는 znz_n에 영향을 주지 않는다. 이러한 문제를 최소화하기 위해서 n과 f의 거리는 가능한 짧아야한다.

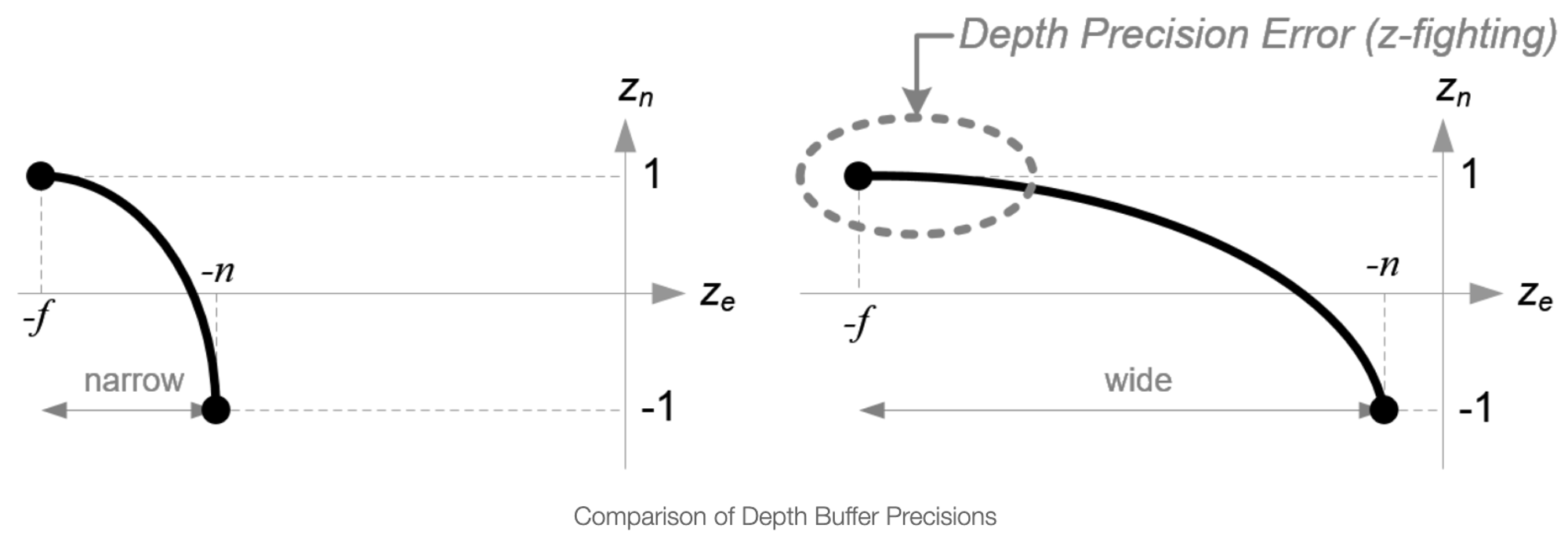
Infinite Perspective Matrix

perspective projection matrix는 far 평면을 행렬의 세번째 행에서 무한대로 설정하여 간단하게 할 수 있다.

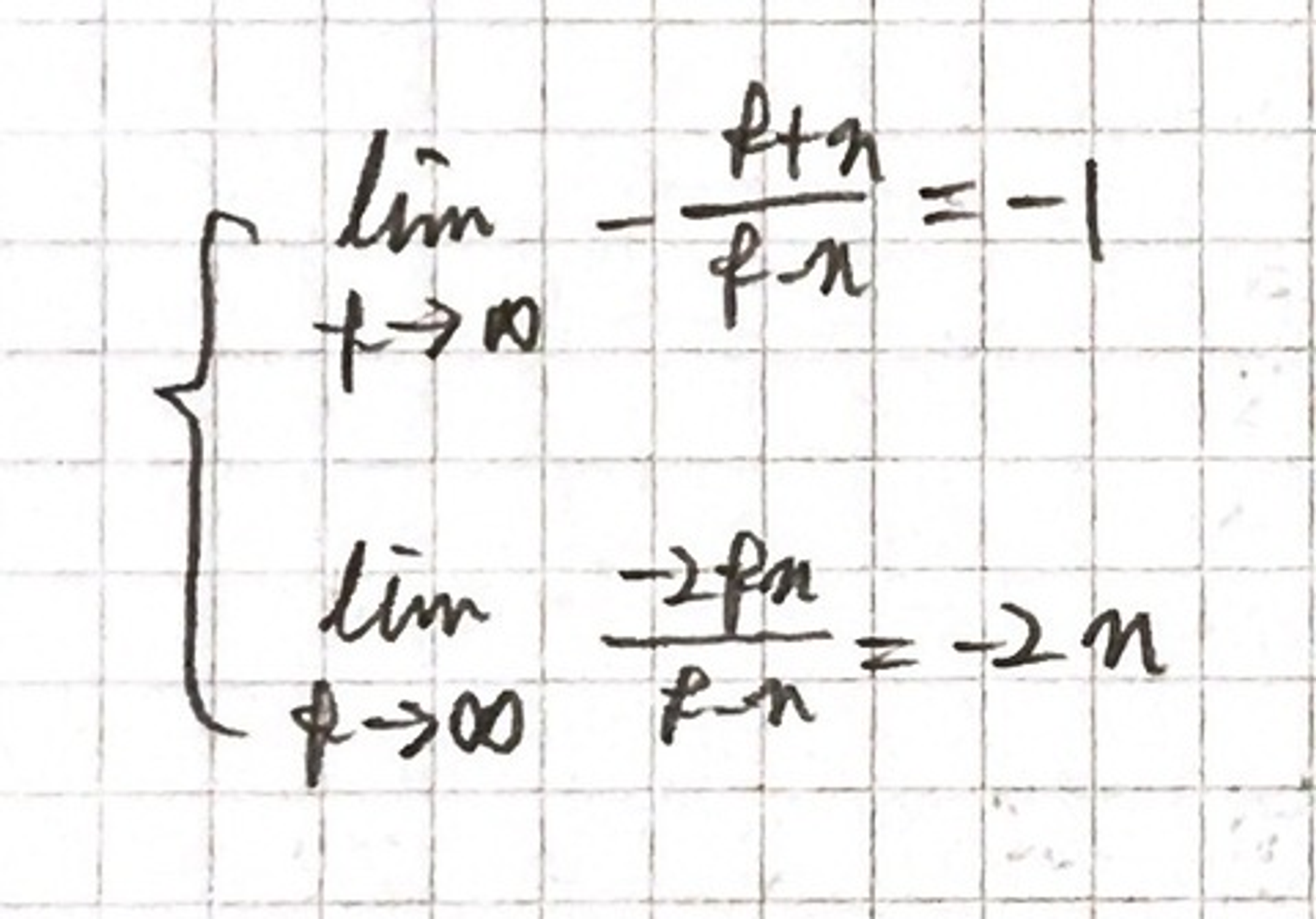
[2nr−l0r+lr−l002nt−bt+bt−b0 00 −1 −2n00 −10]\begin{bmatrix}\frac{2n}{r-l}\quad 0\quad \frac{r+l}{r-l} \quad 0\\ 0\quad\frac{2n}{t-b}\quad \frac{t+b}{t-b}\quad 0\ \\ 0\quad0 \ -1\ -2n\\ 0\quad 0 \ -1\quad 0\end{bmatrix},[nr0000nt00 00 −1 −2n00−10]\begin{bmatrix}\frac{n}{r}\quad 0\quad 0 \quad 0\\ 0\quad\frac{n}{t}\quad 0\quad 0\ \\ 0\quad0 \ -1\ -2n\\ 0\quad 0\quad -1\quad 0\end{bmatrix}

일반 perspective projection matrix와 대칭 perspective projection matirx에 무한 far 평면으로 했을 때 위와 같은 행렬들이 나온다.

이 또한 depth precision error를 갖는다.

Perspective matrix with Field of View(FOV)

특정 창 크기에서 perspective projection에 관한 주어진 near 평면과 far 평면과 4개의 매개변수를 제대로 결정하기 어렵다. 폭과 높이 그리고 수직, 수평의 FOV와 aspect ratio(화면비, 종횡비 등)으로부터 4개의 매개변수를 쉽게 끌어낼 수 있다. 하지만 이는 대칭 perspective projection matrix에서만 가능.

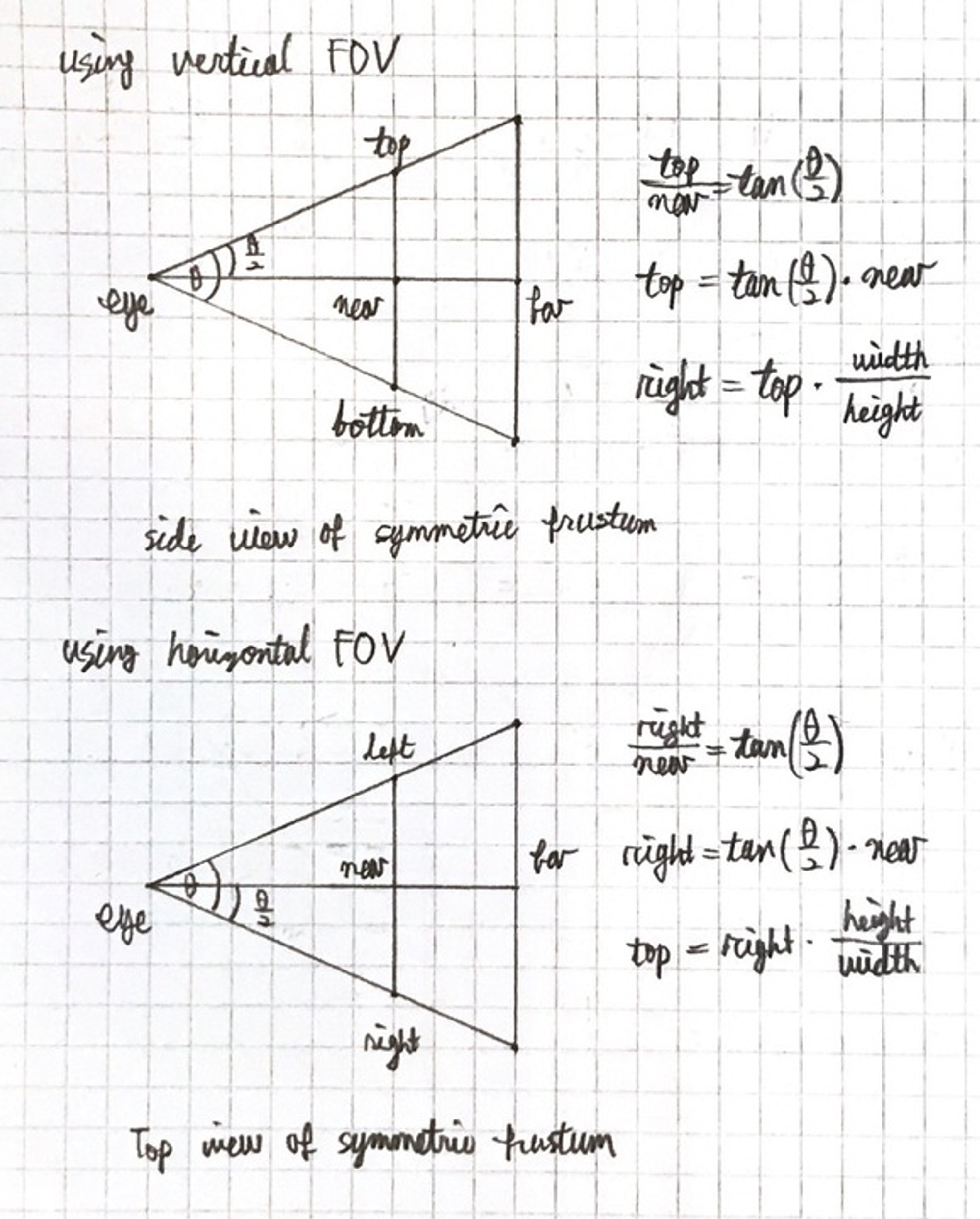
// This creates a symmetric frustum with vertical FOV
// by converting 4 params (fovy, aspect=w/h, near, far)
// to 6 params (l, r, b, t, n, f) 
Matrix4 makeFrustum(float fovY, float aspectRatio, float front, float back)
{
    const float DEG2RAD = acos(-1.0f) / 180;

    float tangent = tan(fovY/2 * DEG2RAD);    // tangent of half fovY
    float top = front * tangent;              // half height of near plane
    float right = top * aspectRatio;          // half width of near plane

    // params: left, right, bottom, top, near(front), far(back)
    Matrix4 matrix;
    matrix[0]  =  front / right;
    matrix[5]  =  front / top;
    matrix[10] = -(back + front) / (back - front);
    matrix[11] = -1;
    matrix[14] = -(2 * back * front) / (back - front);
    matrix[15] =  0;
    return matrix;
}

// This creates a symmetric frustum with horizontal FOV
// by converting 4 params (fovx, aspect=w/h, near, far)
// to 6 params (l, r, b, t, n, f) 
Matrix4 makeFrustum(float fovX, float aspectRatio, float front, float back)
{
    const float DEG2RAD = acos(-1.0f) / 180;

    float tangent = tan(fovX/2 * DEG2RAD);    // tangent of half fovX
    float right = front * tangent;            // half width of near plane
    float top = right / aspectRatio;          // half height of near plane

    // params: left, right, bottom, top, near(front), far(back)
    Matrix4 matrix;
    matrix[0]  =  front / right;
    matrix[5]  =  front / top;
    matrix[10] = -(back + front) / (back - front);
    matrix[11] = -1;
    matrix[14] = -(2 * back * front) / (back - front);
    matrix[15] =  0;
    return matrix;
}

Orthographic projection

Orthographic projection(정투영)에 관한 GL_PROJECTION 구현은 상대적으로 쉽다. view-space의 모든 요소는 NDC와 선형적으로 매핑된다.

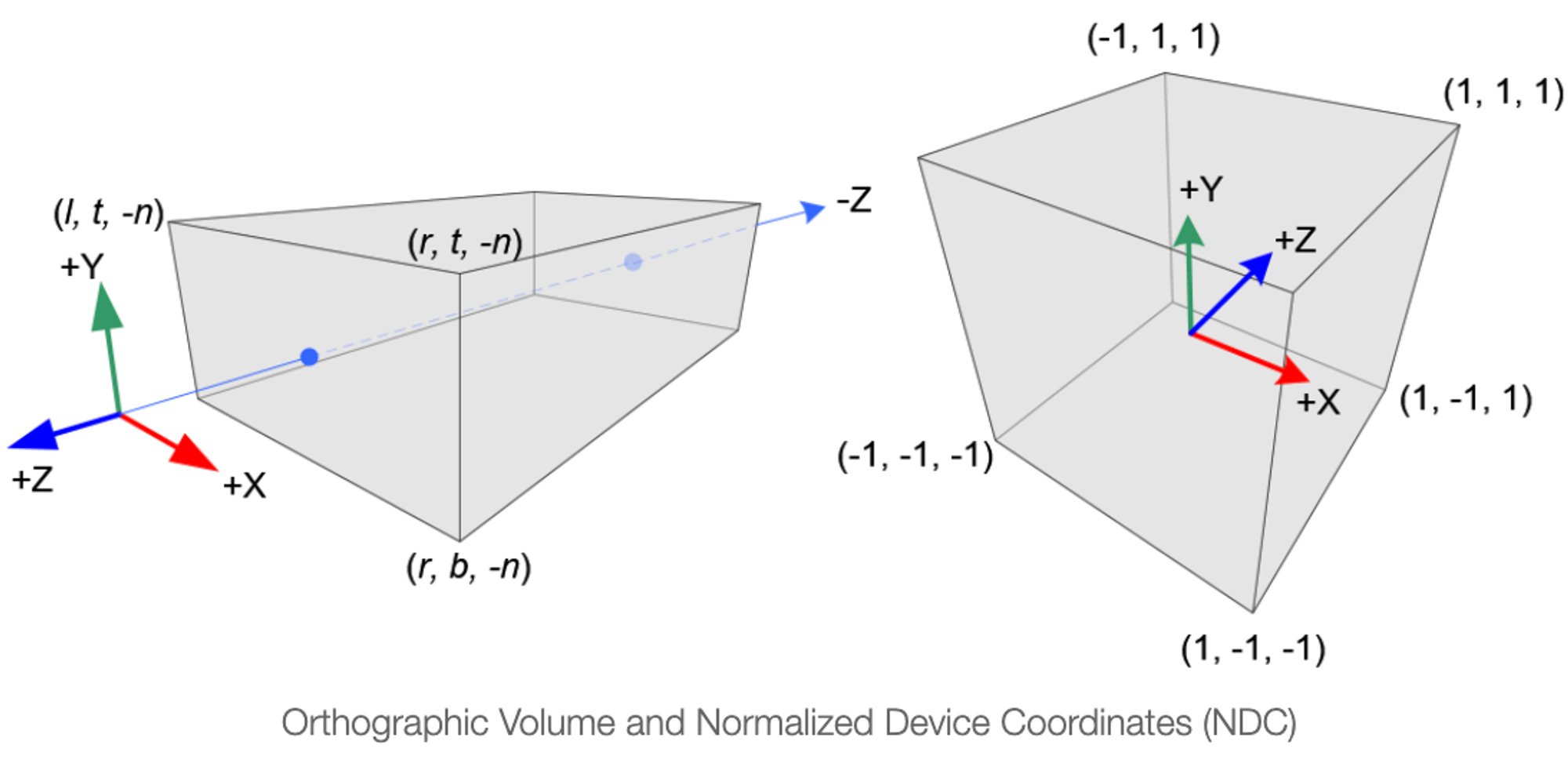
w 요소는 orthographic projection에 필요 없기때문에 네번째 행은 (0, 0, 0, 1)이다.

[2r−l00−r+lr−l02t−b0−t+bt−b00 −2f−n−f+nf−n0 001]\begin{bmatrix}\frac{2}{r-l}\quad 0\quad 0 \quad -\frac{r+l}{r-l}\\ 0\quad\frac{2}{t-b}\quad 0\quad -\frac{t+b}{t-b}\\ 0\quad0 \quad\ \frac{-2}{f-n}\quad -\frac{f+n}{f-n}\\ 0\quad\ 0\quad\quad 0\quad\quad 1\end{bmatrix}

view volume이 대칭이라면 좀 더 간단하게 할 수 있다. r=−1r = -1 그리고 t=−bt = -b

[1r00001t0000−2f−n−f+nf−n0 001]\begin{bmatrix}\frac{1}{r}\quad 0\quad 0 \quad 0\\ 0\quad\frac{1}{t}\quad 0\quad 0\\ 0\quad 0\quad \frac{-2}{f-n} -\frac{f+n}{f-n}\\ 0\quad\ 0\quad 0\quad 1\end{bmatrix}

참고자료 끝

perspective projection matrix는 GLM에서 생성가능하다.

glm::mat4 proj = glm::perspective(glm::radians(45.0f), (float)width /
																	(float)height, 0.1f, 100.0f);

glm::perspective는 큰 절두체를 생성하는데 이는 visible space를 정의하고 clip-space 볼륨에서 벗어난 어느 것도 절두체에서 결과물로 나오지 않고 clip된다.

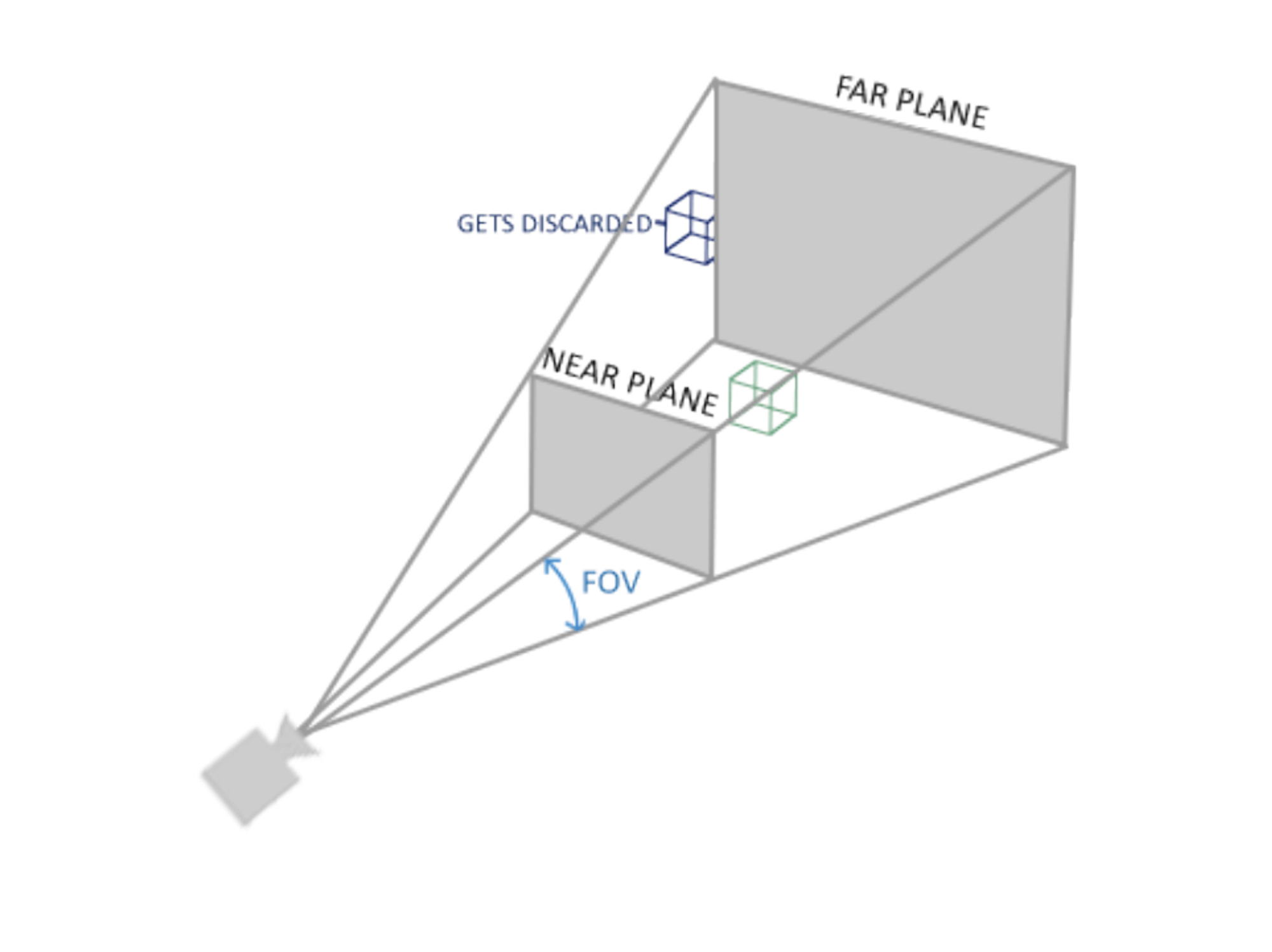
첫번째 매개변수는 FOV를 정의, 이는 field of view의 약어이며 viewspace를 얼마나 크게할지 설정. 사실적인 뷰를 위하여 45도로 설정, 하지만 좀 더 doom-style 결과를 원하면 좀 더 높게 설정할 수 있다. 두번째 매개변수는 aspect ratio(종횡비, 화면비 등)를 설정한다. 이는 viewport의 폭을 높이로 나눈 것으로 계산한다. 세번째와 네번째는 절두체의 near와 far 평면 설정. 보통 near 거리는 0.1 그리고 far 거리는 100.0으로 설정. near와 far 평면의 사이와 절두체 내부의 모든 vertices는 렌더링된다.

perspective 행렬의 near 값이 10.0과 같이 매우 높게 설정될 때마다 OpenGL은 카메라에 가까운 모든 좌표 즉 0과 10.0사이의 좌표들은 clip한다. 이는 아마 비디오게임하면서 경험해봤을 수도 있다. 특정 오브젝트에 가깝게 갔을때 그러한 결과를 볼 수 있다.

orthographic projection을 사용할 때 각 vertex 좌표는 clip space에 바로 매핑된다. orthographic projection은 perspective projection을 사용하지 않으므로 멀리 떨어진 물체들이 더 작게 보이지 않는다. 이는 기괴한 결과물을 보여준다. 이러한 이유로 orthographic projection은 주로 2D 렌더링에서 주로 사용되며 perspective에 의해 삐뚤어진 vertices를 가지지 않는 몇몇 건축학 또는 공학 애플리케이션에서 사용된다. 3D 모델링에 사용되는 Blender 같은 애플리케이션들은 가끔 orthographic projection을 사용하기도 한다. 이는 각 오브젝트들의 치수를 좀 더 정확하게 그리기 위함이다. Blender에서 두 projection을 한 경우를 보면 vertex간의 간격이 다르다.

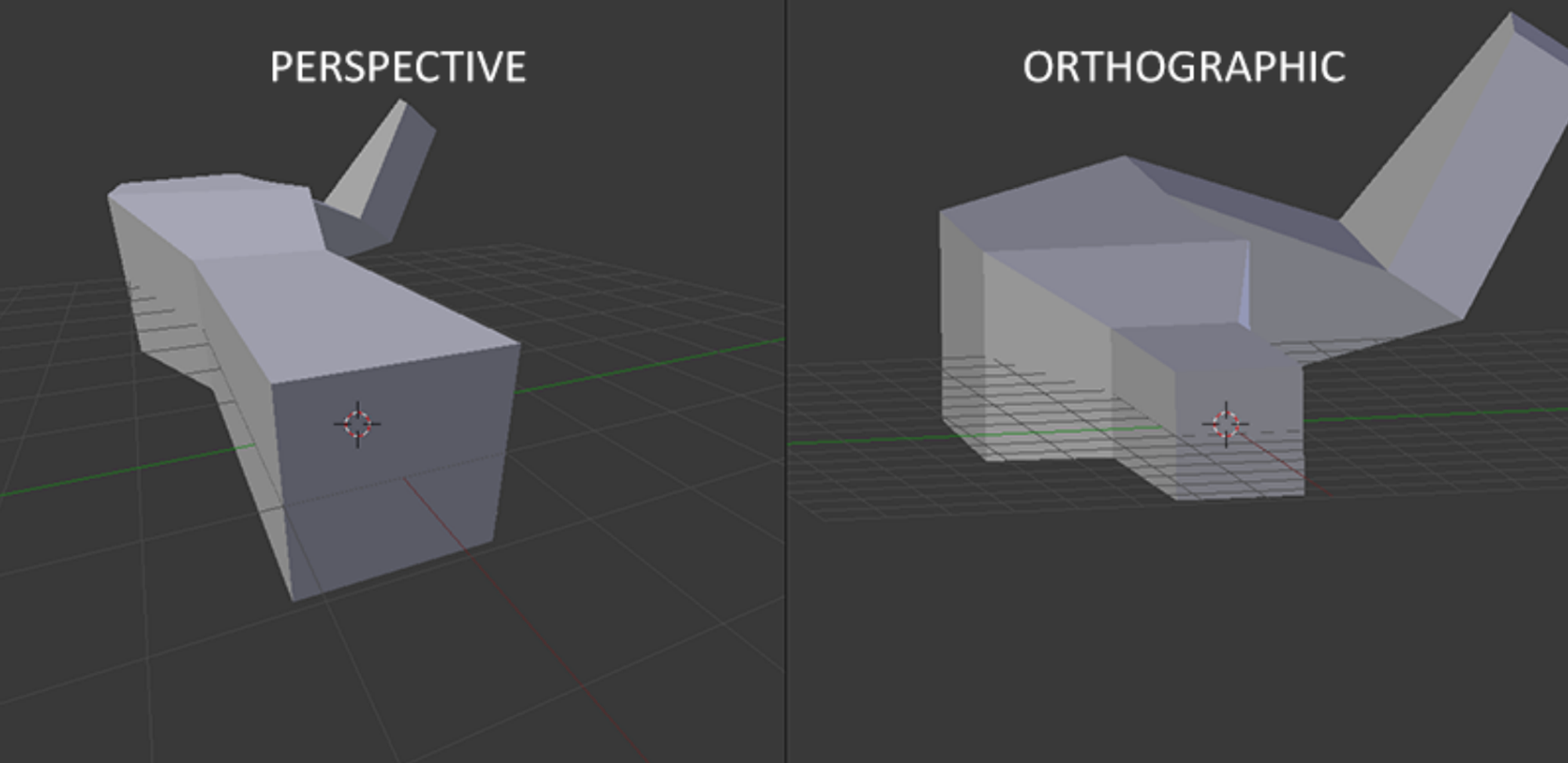
Putting it all together

앞서 언급한 단계들 각각에 관한 변환 행렬들을 만들었다: model, view, projection matrix. vertex 좌표들은 이제 clip 좌표로 변환된다.

Vclip=Mprojection⋅Mview⋅Mmodel⋅VlocalV_{clip} = M_{projection}\cdot M_{view}\cdot M_{model}\cdot V_{local}.

행렬 곱셈의 순서는 뒤집힌다. 행렬 곱셈을 왼쪽에서 오른쪽으로 하는 것을 기억하자. 이 결과로 나온 vertex들은 vertex shader에 있는 gl_Position에 할당되고 OpenGL은 자동으로 perspective division과 clipping을 수행한다.

  • vertex shader의 출력값은 clip-space 좌표로 되기 위한 변환된 좌표를 요구하고 OpenGL을 clip-space 좌표들을 perspective division을 수행하고 NDC로 변환한다. 그리고 OpenGL은 glViewport로부터 매개변수를 사용하는데 이는 NDC를 screen 좌표로 매핑하기 위함이다. 이 처리는 viewport transformation이라 한다.

Going 3D

2D에서 3D로 바꿔볼 것.

3D로 그리기위해서 먼저 model 행렬을 생성한다. model 행렬은 모든 오브젝트들의 vertices를 global world space로 변환을 적용하기 원하는 이동, 크기 조정, 회전들로 구성되어있다.

glm::mat4 model = glm::mat4(1.0f);
model = glm::rotate(model, glm::radians(-55.0f), glm::vec3(1.0f, 0.0f, 0.0f));

vertex 좌표를 model 행렬에 곱하여 vertex 좌표를 world space 좌표로 변환한다.

그 다음 view 행렬을 만든다. scene을 살짝 뒤로 움직여서 물체를 보이게 한다.

  • 카메라를 뒤로 움직이는 것은 전체 scene을 앞으로 움직이는 것과 같다.

OpenGL은 오른손 좌표계이므로 -z 방향은 앞으로 이동, z방향은 뒤로 이동이다. scene을 -z 방향으로 움직인다.

scene 주위를 움직이는 것은 다음 챕터에서 자세히 다룰 것이고 여기서는 아래의 코드로 설정

glm::mat4 view = glm::mat4(1.0f);
// note that we’re translating the scene in the reverse direction
view = glm::translate(view, glm::vec3(0.0f, 0.0f, -3.0f));

마지막으로 projection 행렬 정의한다. perspective projection을 사용할 것이며 설정은 아래와 같다.

glm::mat4 projection;
projection = glm::perspective(glm::radians(45.0f), 800.0f / 600.0f, 0.1f, 100.0f);

이제 변환 행렬들을 다 만들었고 shader에게 전달한다. 먼저 vertex shader에서 uniform으로 변환 행렬들을 설정하고 vertex 좌표들과 곱한다.

#version 330 core
layout (location = 0) in vec3 aPos;
...
uniform mat4 model;
uniform mat4 view;
uniform mat4 projection;

void main()
{
	// note that we read the multiplication from right to left
	gl_Position = projection * view * model * vec4(aPos, 1.0);
	...
}

이제 변환 행렬들을 shader로 보낸다.

int modelLoc = glGetUniformLocation(ourShader.ID, "model");
glUniformMatrix4fv(modelLoc, 1, GL_FALSE, glm::value_ptr(model));
... // same for View Matrix and Projection Matrix

이제 vertex 좌표를 model, view, projection 행렬을 통해서 변환된다. 그 결과물은 아래와 같다.

  • 바닥과 뒤쪽으로 기울어졌다.
  • 조금 멀리 떨어져있다.
  • 원근감있다.

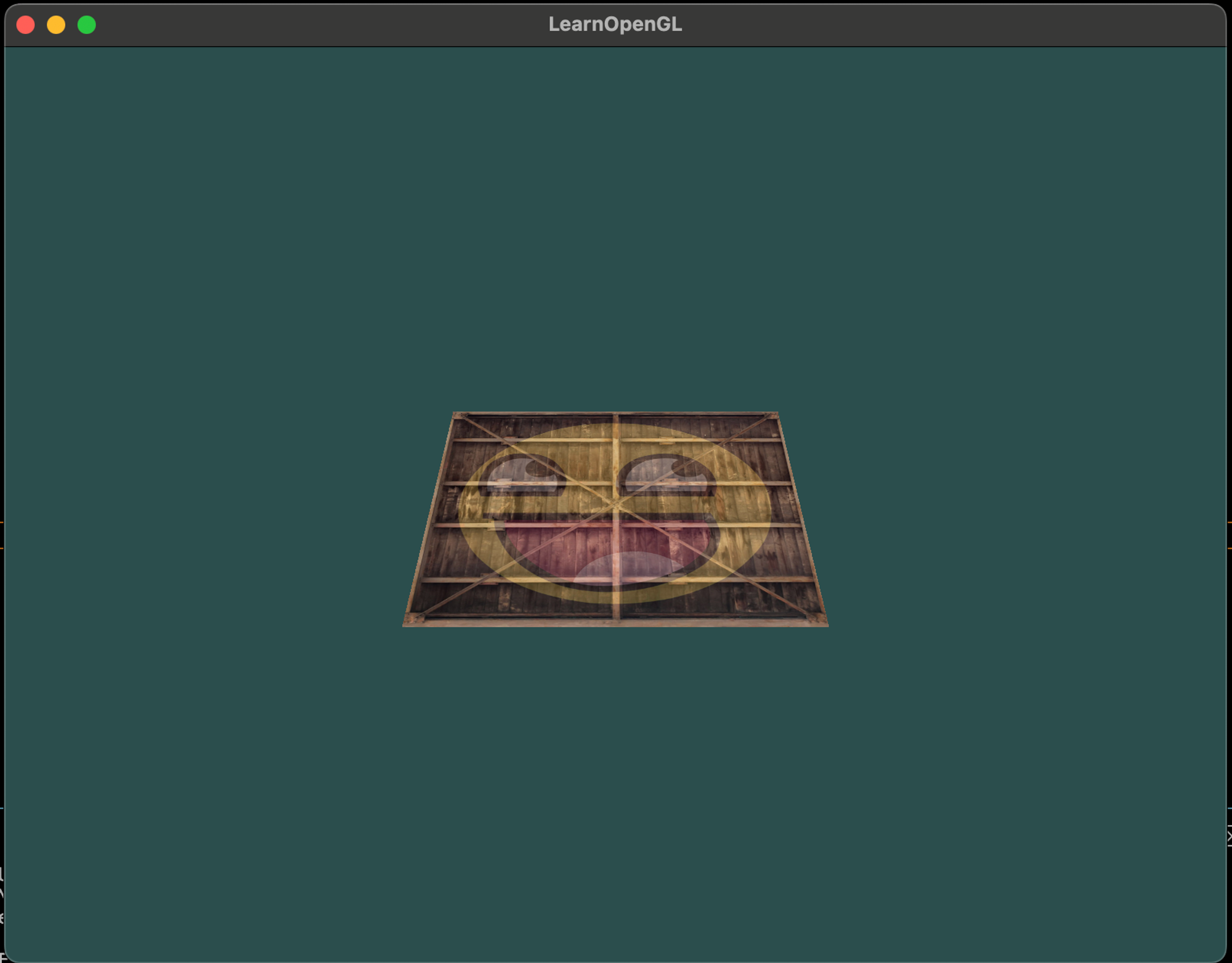
More 3D

지금까지 3차원 공간에서 2차원 평면을 가지고 작업했다. 이제 2차원 평면을 3차원 큐브로 확장한다. 큐브를 렌더링하기 위해서 총 36개의 vertices(6 faces 2 triangle 3 vertices) 필요. 

    float vertices[] = {
        -0.5f, -0.5f, -0.5f,  0.0f, 0.0f,
         0.5f, -0.5f, -0.5f,  1.0f, 0.0f,
         0.5f,  0.5f, -0.5f,  1.0f, 1.0f,
         0.5f,  0.5f, -0.5f,  1.0f, 1.0f,
        -0.5f,  0.5f, -0.5f,  0.0f, 1.0f,
        -0.5f, -0.5f, -0.5f,  0.0f, 0.0f,

        -0.5f, -0.5f,  0.5f,  0.0f, 0.0f,
         0.5f, -0.5f,  0.5f,  1.0f, 0.0f,
         0.5f,  0.5f,  0.5f,  1.0f, 1.0f,
         0.5f,  0.5f,  0.5f,  1.0f, 1.0f,
        -0.5f,  0.5f,  0.5f,  0.0f, 1.0f,
        -0.5f, -0.5f,  0.5f,  0.0f, 0.0f,

        -0.5f,  0.5f,  0.5f,  1.0f, 0.0f,
        -0.5f,  0.5f, -0.5f,  1.0f, 1.0f,
        -0.5f, -0.5f, -0.5f,  0.0f, 1.0f,
        -0.5f, -0.5f, -0.5f,  0.0f, 1.0f,
        -0.5f, -0.5f,  0.5f,  0.0f, 0.0f,
        -0.5f,  0.5f,  0.5f,  1.0f, 0.0f,

         0.5f,  0.5f,  0.5f,  1.0f, 0.0f,
         0.5f,  0.5f, -0.5f,  1.0f, 1.0f,
         0.5f, -0.5f, -0.5f,  0.0f, 1.0f,
         0.5f, -0.5f, -0.5f,  0.0f, 1.0f,
         0.5f, -0.5f,  0.5f,  0.0f, 0.0f,
         0.5f,  0.5f,  0.5f,  1.0f, 0.0f,

        -0.5f, -0.5f, -0.5f,  0.0f, 1.0f,
         0.5f, -0.5f, -0.5f,  1.0f, 1.0f,
         0.5f, -0.5f,  0.5f,  1.0f, 0.0f,
         0.5f, -0.5f,  0.5f,  1.0f, 0.0f,
        -0.5f, -0.5f,  0.5f,  0.0f, 0.0f,
        -0.5f, -0.5f, -0.5f,  0.0f, 1.0f,

        -0.5f,  0.5f, -0.5f,  0.0f, 1.0f,
         0.5f,  0.5f, -0.5f,  1.0f, 1.0f,
         0.5f,  0.5f,  0.5f,  1.0f, 0.0f,
         0.5f,  0.5f,  0.5f,  1.0f, 0.0f,
        -0.5f,  0.5f,  0.5f,  0.0f, 0.0f,
        -0.5f,  0.5f, -0.5f,  0.0f, 1.0f
    };

재미를 위해서 큐브를 회전 시킨다.

model = glm::rotate(model, (float)glfwGetTime() * glm::radians(50.0f),
glm::vec3(0.5f, 1.0f, 0.0f));

glDrawArrays을 사용하여 큐브를 그리는데 지금은 36개의 vertices을 사용하므로 이에 맞게 설정.

glDrawArrays(GL_TRIANGLES, 0, 36);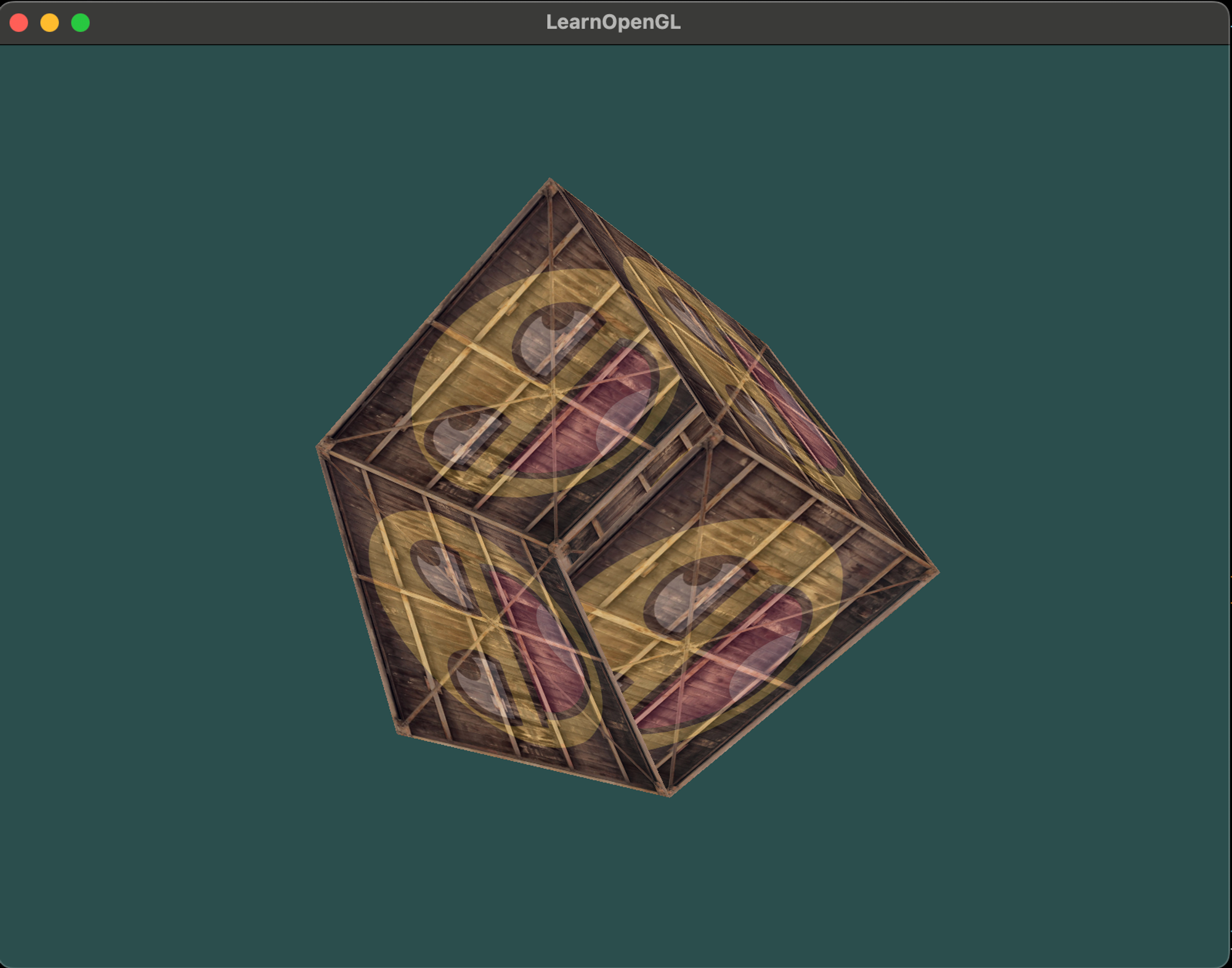


큐브처럼 보이지만 무언가 잘못됐다. 이는 OpenGL이 triangle by triagle, fragment by fragment으로 그리고 이는 이전에 그려진 픽셀을 덮어 겹쳐 그려진다. OpenGL은 draw 함수 호출에서 렌더링된 삼각형들의 순서를 고려하지 않기때문에 다른 삼각형보다 앞에 있는 삼각형이 있음에도 그 위에 삼각형들이 그려진다.

OpenGL이 겹쳐 그릴지 말지 결정하게 해주는 z-buffer라 불리는 버퍼에 depth information(깊이 정보)를 저장한다. z-buffer를 사용하여 OpenGL이 depth-testing(깊이 테스트)를 할 수 있게 설정할 수 있다.

Z-buffer

OpenGL은 depth buffer라 불리는 z-buffer에 depth 정보를 저장한다. GLFW는 자동으로 이런 버퍼를 생성한다(출력 이미지의 색상을 저장하는 color-buffer를 가지는 것과 같다). depth는 각 fragment(fragment의 z값)에 저장되며 fragment가 색상을 출력하기 원할 때마다 OpenGL은 z-buffer와 fragment의 z 값을 비교한다. 만약 현재 fragment가 다른 fragment에 뒤에 있으면 현재의 것이 버려진다. 아닌 경우 덮어쓰여진다. 이러한 처리를 depth-testing이라 하며 OpenGL에 의해서 자동으로 수행된다.

OpenGL이 실제 depth testing을 수행하는지 확실하게 하고 싶으면 먼저 OpenGL이 depth testing을 가능하게 해야한다. 왜냐하면 기본값은 가능하지 않게 되어 있다. glEnable을 사용하여 설정한다. glEnable과 glDisable 함수는 OpenGL에서 특정 기능들을 사용 가능하게 하거나 사용 못하게 할 수 있다. 이 함수들로 설정한 부분들을 다시 설정할 함수들이 나와 설정을 변경할 때까지 설정 값들이 유지된다. GL_DEPTH_TEST를 가능하게 해준다.

glEnable(GL_DEPTH_TEST);

depth 버퍼를 사용하기때문에 렌더 루프에서 매번 depth 버퍼를 정리해야한다. 아니면 depth 정보가 이전 프레임에 관한 것으로 남아있다. 이는 색상 버퍼를 정리해주는 것과 같다. glClear에 DEPTH_BUFFER_BIT을 명시하면 된다.

glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);

아래와 같이 깔끔한 큐브가 나온다.

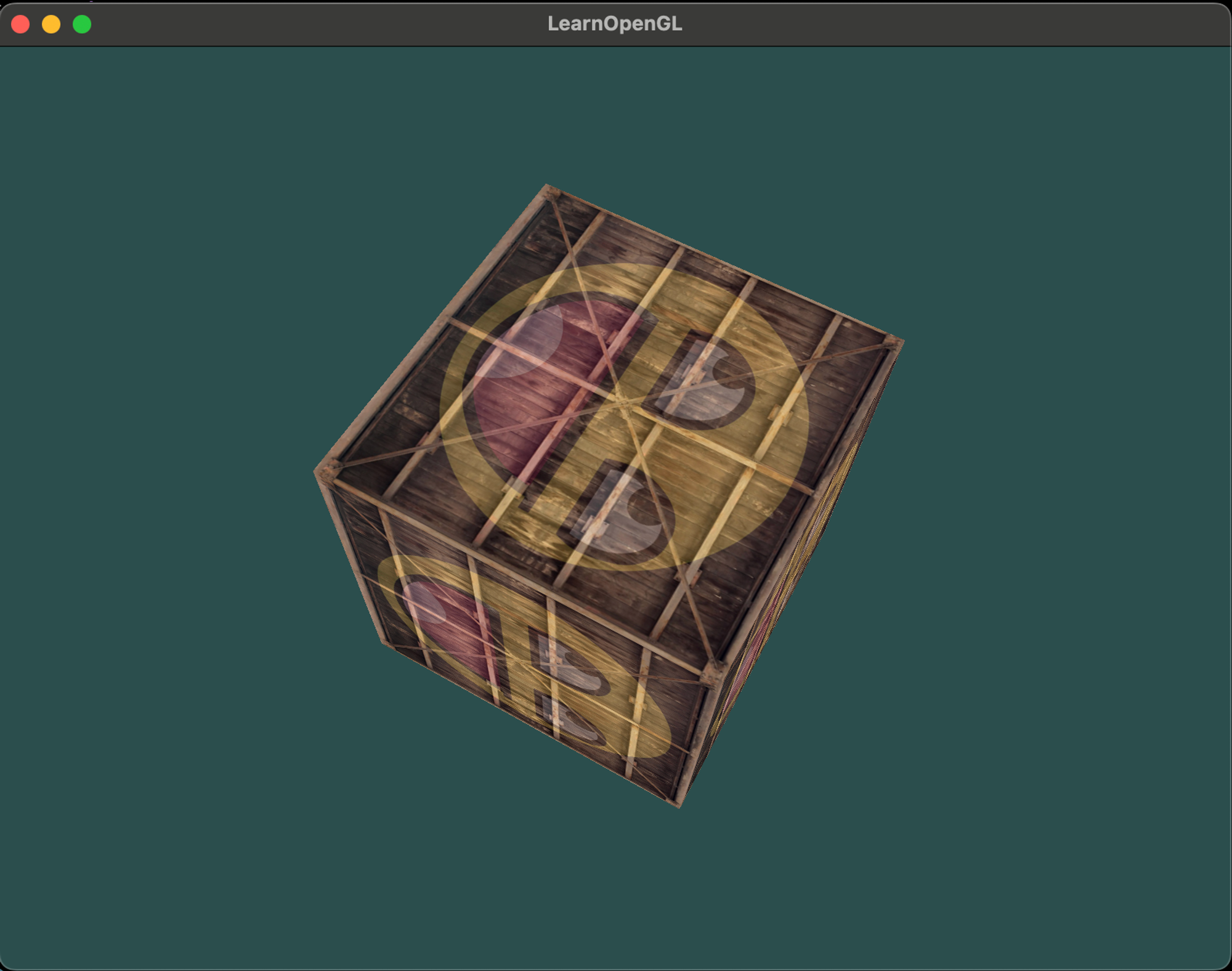
More cubes

10개의 큐브들을 이제 스크린에 나타내보자. 각 큐브는 똑같지만 회전과 world-space에서의 위치가 다르다. 그래픽적인 레이아웃은 이미 정의되어있으므로 버퍼와 attribute array는 바꿀 필요가 없다. 해야할 것은 각 오브젝트들을 world-space로 model 행렬을 통해 변환하는 것.

먼저 world-space에서 각 큐브에 관한 이동 벡터에 대한 위치를 정의. 10개의 큐브 위치를 glm::vec3 배열에 정의.

glm::vec3 cubePositions[] = {
	glm::vec3( 0.0f, 0.0f, 0.0f),
	glm::vec3( 2.0f, 5.0f, -15.0f),
	glm::vec3(-1.5f, -2.2f, -2.5f),
	glm::vec3(-3.8f, -2.0f, -12.3f),
	glm::vec3( 2.4f, -0.4f, -3.5f),
	glm::vec3(-1.7f, 3.0f, -7.5f),
	glm::vec3( 1.3f, -2.0f, -2.5f),
	glm::vec3( 1.5f, 2.0f, -2.5f),
	glm::vec3( 1.5f, 0.2f, -1.5f),
	glm::vec3(-1.3f, 1.0f, -1.5f)
};

렌더 루프에서 glDrawArrays 10번 불러야하지만 이번에 draw call 보내기전에 다른 model 행렬을 vertex shader에 보낸다. 다른 model 행렬을 오브젝트를 10번 그리는 렌더 루프안에 작은 루프문을 매번 생성한다. 또한 각 컨테이너에 작은 특정 회전을 추가한다.

glBindVertexArray(VAO);
for(unsigned int i = 0; i < 10; i++)
{
	glm::mat4 model = glm::mat4(1.0f);
	model = glm::translate(model, cubePositions[i]);
	float angle = 20.0f * i;
	model = glm::rotate(model, glm::radians(angle),
	glm::vec3(1.0f, 0.3f, 0.5f));
	ourShader.setMat4("model", model);
	glDrawArrays(GL_TRIANGLES, 0, 36);
}

위 코드는 매번 새로운 큐브가 그려질 때 model 행렬을 업데이트를 총 10번한다. 아래의 결과물을 갖는다.

profile
김경주
Hello everyone
이전 포스트

OpenGL_06, Transformations

다음 포스트

OpenGL_08, Camera

0개의 댓글