OpenGL_06, Transformations

김경주·2024년 4월 16일

목록 보기

7/10

물체를 만들고 색상을 입히고 이것들에 대해 texture들을 사용하여 좀 더 세부적으로 나타내기까지 했다. 다만 이들은 정적인 물체들이다. 이 object들에 대해서 각 buffer frame을 재설정하고 vertex들(vertices)을 바꾸는 것으로 변화를 줄 수 있지만 이는 비용도 크고 상당히 성가시다. 행렬 object를 사용하여 물체의 transform(변화)를 주는 더 좋은 방식이 있다.

행렬은 매우 강력한 수학적 개념들이다. 처음엔 매우 어려워 보인다. 그렇지만 익숙해지면 매우 유용한 것을 알 수 있다. 몇몇 수학적 지식들에 뛰어들어야하고 이에 더 알아보기 원하면 여러 자료들을 찾아보면 된다.

transformation에 대한 완전한 이해를 위해서 행렬에 관해 얘기하기전에 먼저 벡터에 관해 좀 더 깊이 있게 탐구해야한다. 이 챕터는 후에 나오는 개념들을 이해하기 위해서 기본적인 수학적 개념들을 배운다. 조금 어렵다고 느껴지면 계속해서 이 챕터로 돌아와서 복습하면 된다.

기본적으로 Learn OpenGL의 책을 따라가면서 정리하는데 여기서는 수학적 개념을 설명하기에 여기서 나오는 개념들을 개인적으로 정리한 부분이 크다.

주로 벡터와 행렬, 즉 선형대수학인데 여기서 나오는 부분들만, 순서대로 개인적으로 알아보고 참고한 자료들로 채움.

벡터

공간벡터

행렬

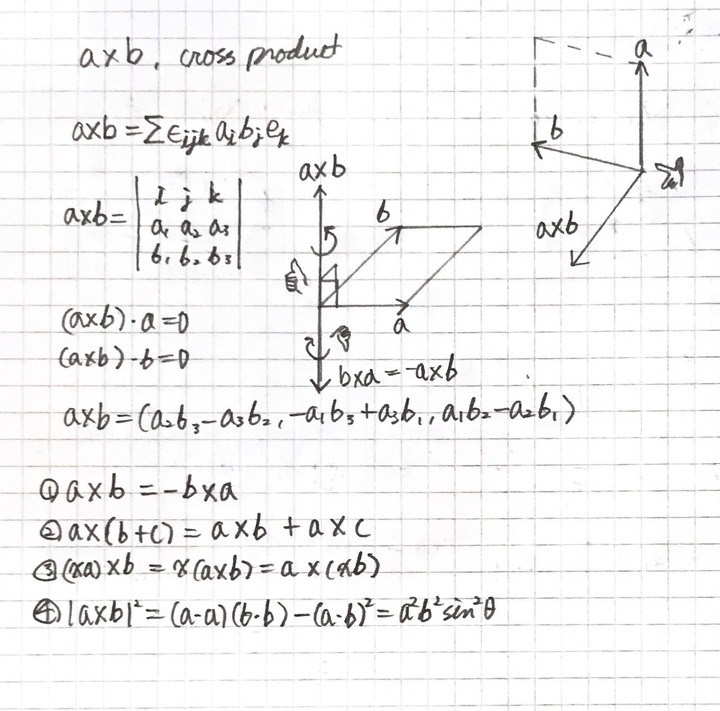
외적 Cross Product

외적은 삼차원 공간에서만 정의된다. 평행하지 않는 두 벡터를 받아서 두 벡터에 수직인 벡터를 산출한다. 만약 두 벡터가 수직이라면 결과로 나오는 벡터 포함하여 모든 벡터가 수직이다.

삼차식의 행렬의 기하학적 정의를 보면 외적에 의미를 조금 쉽게 볼 수 있다. 이차식의 행렬은 평행사변형의 면적이고 삼차식의 행렬은 평행육면체의 부피이다. 부피를 구할 때 한 면과 높이의 곱인데 그 높이를 구하기 위해서 외적의 결과가 필요하다.

행렬식의 성질 중에서 행렬을 각각의 벡터로 가지고 그 벡터 중 중복되는 벡터가 있으면 행렬식은 0이된다. 만약 삼차식의 행렬 $M(\vec{a}, \vec{b}, \vec{c})$ 이 있을 때 그리고 벡터 $\vec{u}$ 를 $\begin{bmatrix}a_2b_3-a_3b_2 \\ a_3b_1-a_1b_3\\a_1b_2-a_2b_1\end{bmatrix}$ 로 놓으면(참고로 이게 외적의 결과다.) $\vec{c}$ 에 $\vec{a}$ 나 $\vec{b}$ 를 놓으면 행렬식의 성질에 따라 행렬식은 0이 나온다. 이는 $\vec{u}\cdot \vec{a} = 0$ 과 $\vec{u}\cdot \vec{b} = 0$ 으로 나타난다. 이는 벡터 $\vec{u}$ 가 두 벡터와 직교하고 두 벡터의 평행사변형에 수직이라는 것
외적의 성질

항등 행렬(Identity Matrix)

가장 간단한 변환 행렬은 항등 행렬이라고 생각할 수 있다. 항등 행렬은 대각에 있는 성분을 제외하고 0인 NxN 행렬을 말한다.

$\begin{bmatrix}1\ 0\ 0\ 0\\ 0\ 1\ 0\ 0\\0\ 0\ 1\ 0 \\0\ 0\ 0\ 1\end{bmatrix} \cdot \begin{bmatrix}1\\2\\3 \\4\end{bmatrix} = \begin{bmatrix}1 \cdot 1\\1 \cdot 2\\1 \cdot 3\\1 \cdot 4\end{bmatrix} = \begin{bmatrix}1\\2\\3 \\4\end{bmatrix}$

어디서 사용? 항등 행렬은 다른 변환 행렬을 만들기 위한 시작점

추가

대칭 이동 $\begin{bmatrix}1\quad 0\\\ 0\ -1\end{bmatrix} \cdot \begin{bmatrix}x\\y\end{bmatrix} = \begin{bmatrix}x^\prime \\ y^\prime\end{bmatrix}$ x축에 관한 대칭 이동 $\begin{bmatrix}-1\quad 0\\\ 0\ -1\end{bmatrix} \cdot \begin{bmatrix}x\\y\end{bmatrix} = \begin{bmatrix}x^\prime \\ y^\prime\end{bmatrix}$ 원점에 관한 대칭 이동 $\begin{bmatrix}-1\quad 0\\\ 0\quad 1\end{bmatrix} \cdot \begin{bmatrix}x\\y\end{bmatrix} = \begin{bmatrix}x^\prime \\ y^\prime\end{bmatrix}$ y축에 관한 대칭 이동 $\begin{bmatrix}\ 1\ 0\\\ 0\ 1\end{bmatrix} \cdot \begin{bmatrix}x\\y\end{bmatrix} = \begin{bmatrix}x^\prime \\ y^\prime\end{bmatrix}$ y = x 선분에 관한 대칭 이동

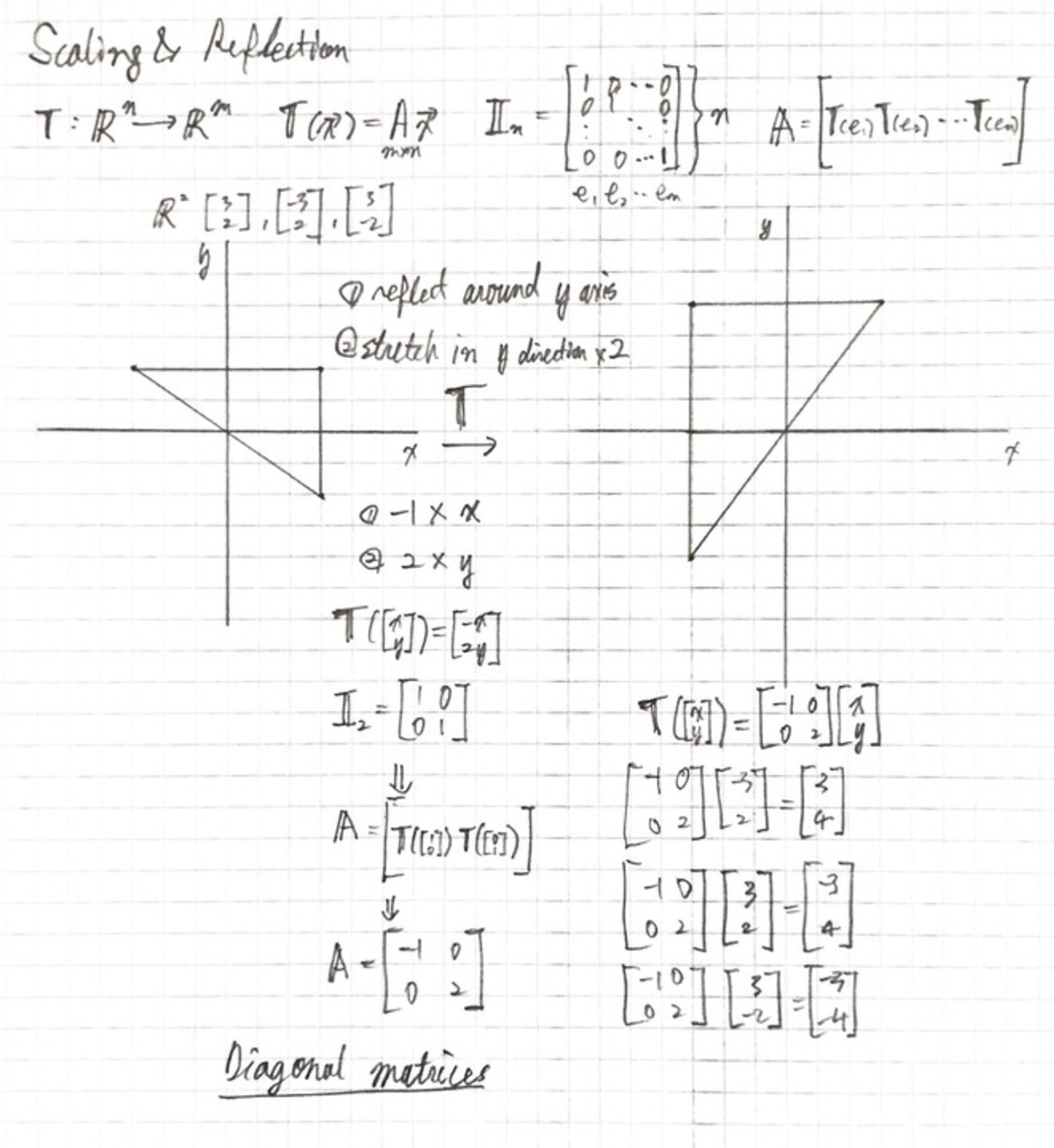
Scaling

벡터의 크기를 조정할 때, 원하는 크기의 양만큼 같은 방향을 유지하면서 길이를 증가할 벡터의 크기를 증가시킨다. 이차원이나 삼차원 벡터 둘 중 하나로 작업하므로 이차원이나 삼차원 scaling 변수에 의해 정의할 수 있다.

$\vec{v} = \begin{bmatrix} 3\\2 \end{bmatrix}$ 를 x축으로 0.5, 즉 두 배로 줄이고 y축으로 2, 두배로 늘리면 $\vec{v} = \begin{bmatrix} 1.5\\4 \end{bmatrix}$ 가 된다. OpenGL은 보통 이차원 경우에도 삼차원 공간에서 작동되므로 z축을 1로 둔다. 이러한 연산을 non-uniform scale인데 왜냐하면 각축에 대한 scaling 요소(factors)들이 똑가지 않기 때문. 만약 각축에 대한 스칼라가 같으면 uniform scale이라 부른다.

이제 위의 항등 행렬 1들을 바꾸면 scaling matrix를 만들 수 있다. 마지막은 1은 그냥 둔다.

$\begin{bmatrix}S_1\ 0\ 0\ 0\\ 0\ S_2\ 0\ 0\\0\ 0\ S_3\ 0 \\0\ 0\ 0\ 1\end{bmatrix} \cdot \begin{bmatrix}x\\y\\z \\1\end{bmatrix} = \begin{bmatrix}S_1 \cdot x\\S_2 \cdot y\\S_3 \cdot z\\1 \cdot 1\end{bmatrix} = \begin{bmatrix}S_1\\S_2\\S_3 \\1\end{bmatrix}$

역행렬을 구하는 프로세스를 기하학적으로 간단하게

$\begin{bmatrix}\ \frac{1}{S_1}\ 0\ 0\ 0\\ \ 0\ \frac{1}{S_2}\ 0\ 0\\ \ 0\ 0\ \frac{1}{S_3}\ 0 \\ \ 0\ \ 0\ \ 0\ \ 1\end{bmatrix}$ 이렇게 역행렬을 만들 수 있다.

Translation

Translation은 다른 위치를 가진 새로운 벡터를 반환하기위해 기존 벡터에 다른 벡터를 더하는 과정 translation 벡터를 토대로 벡터를 움직이는 것.

4x4 행렬에 3개의 요소 값을 넣어서 특정 연산을 수행. Translation 벡터를 $(T_x, T_y, T_z)$ 로 나타내면 translation 행렬을 다음과 같이 정의할 수 있다.

$\begin{bmatrix}1\ 0\ 0\ T_x\\ 0\ 1\ 0\ T_y\\0\ 0\ 1\ T_z\\0\ 0\ 0\ 1\end{bmatrix} \cdot \begin{bmatrix}x\\y\\z \\1\end{bmatrix} = \begin{bmatrix}x+T_x\\y+T_y\\z+T_z\\1\end{bmatrix}$

translation 값들은 벡터의 w열에 의해 곱해지고 벡터의 원래 값에 더해진다. 이는 3x3 행렬에는 불가능.

벡터의 w의 요소는 동차 좌표계(homogeneous coordinate)라 알려져있다. homogeneous 벡터로부터 3차원 벡터를 갖기 위해서 x, y, z를 w 좌표로 나눈다. 보통 w 요소가 1.0이기에 이를 신경쓰지 않음. 동차좌표계를 쓰는 것은 몇 가지 이점이 있다. 삼차원 벡터에서 행렬 translation을 할 수 있고 다음 장에서 w 값을 3D perspective를 생성하기 위해 사용한다. 동차 좌표계가 0이라면 그 벡터가 방향 벡터라는 것을 말해준다. 왜냐하면 0이여서 translation이 불가하기때문이다.

이동의 역행렬은 마지막 열의 세가지 원소의 값이 음수면 된다.

Rotation

이번 변환 행렬은 위 항등 행렬과 이동 행렬과는 달리 상대적으로 어렵다.

Khan Academy

Linear Algebra | Khan Academy

벡터의 rotation? 2D나 3D에서 rotation은 angle(각)으로 표현된다. 각은 도나 라디안으로 표현 가능. 여기서는 도로 설명.

라디안에서 도로 변환하는 것은 어렵지 않다.

PI = 3.14159265359
angle_in_degrees = angle_in_radians * (180 / PI)
angle_in_radians = angle_in_degrees * (PI / 180)

반원을 회전하는 것은 180도, 원의 1/5 오른쪽 회전은 72도로 오른쪽으로 회전. 그림은 2차원 벡터 $\vec{k}$ 에서 1/5 오른쪽으로 회전했을때 $\vec{v}$ 를 나타낸다.

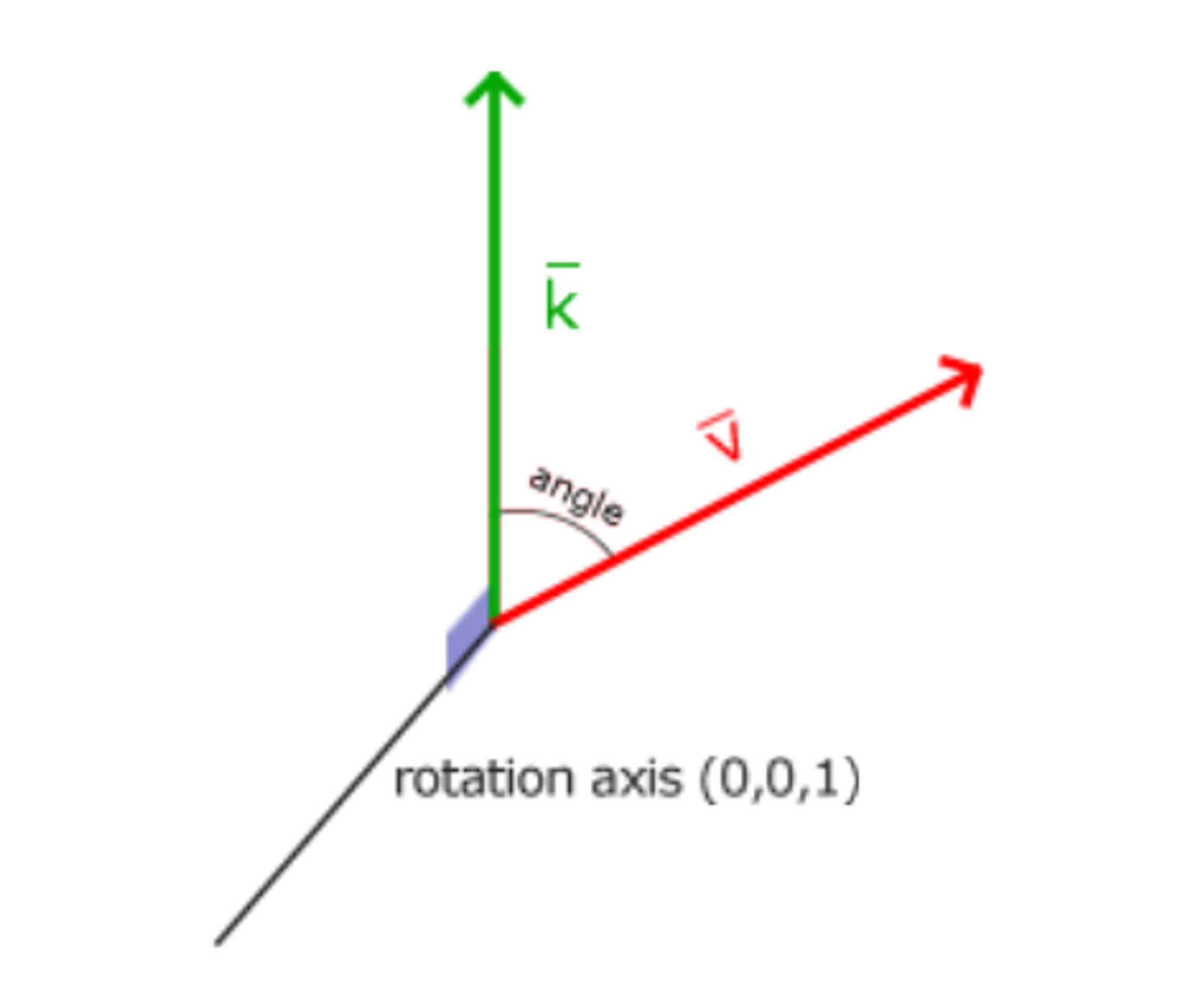
삼차원에서 회전은 각과 회전축으로 명시된다. 명시된 각은 주어진 회전축을 따라 물체를 회전시킨다. 삼각함수를 사용하여 벡터를 주어진 각에 맞게 새롭게 회전된 벡터들로 변환 가능하다.

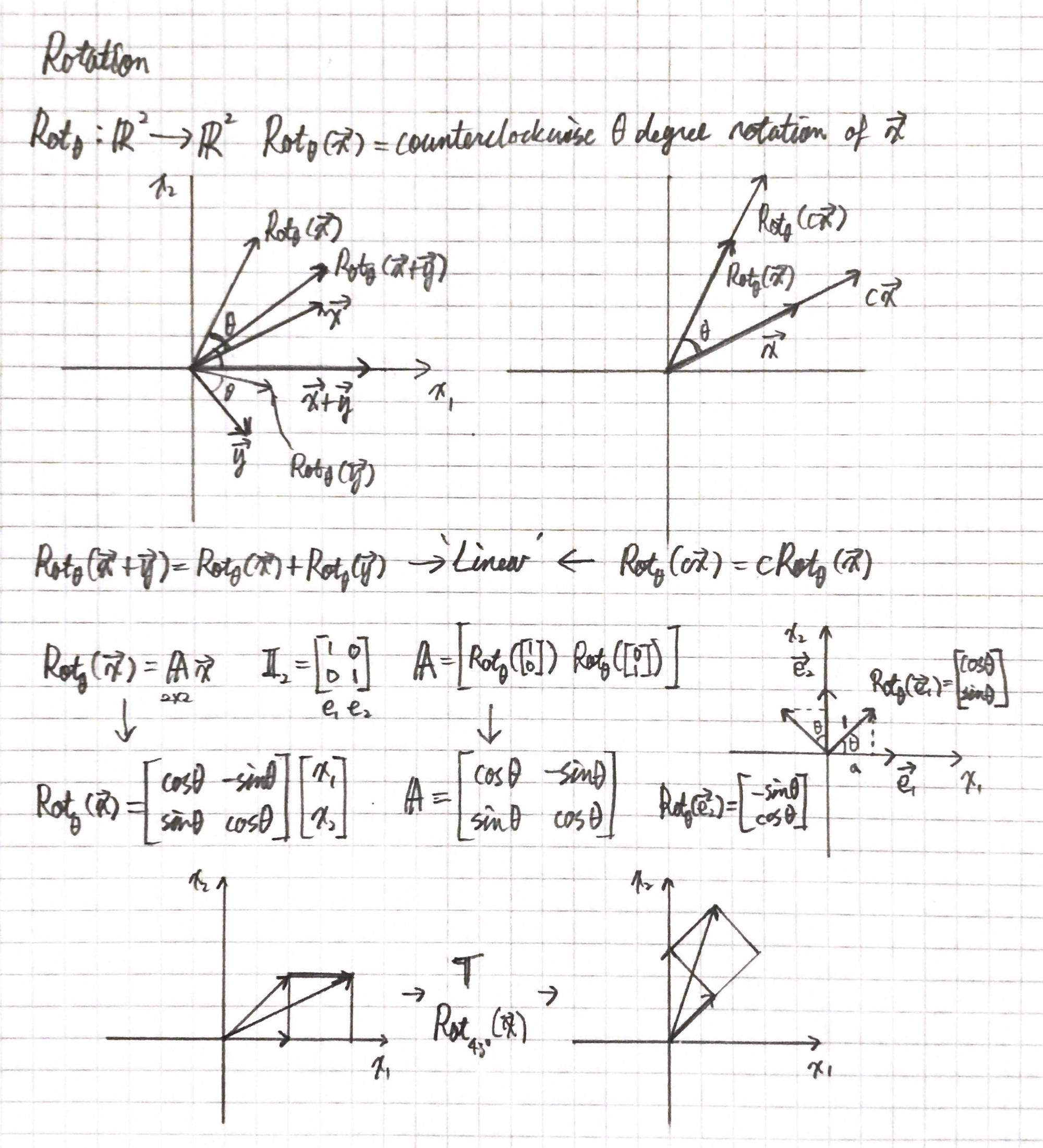
회전 변환의 선형성 만족 → 선형 변환

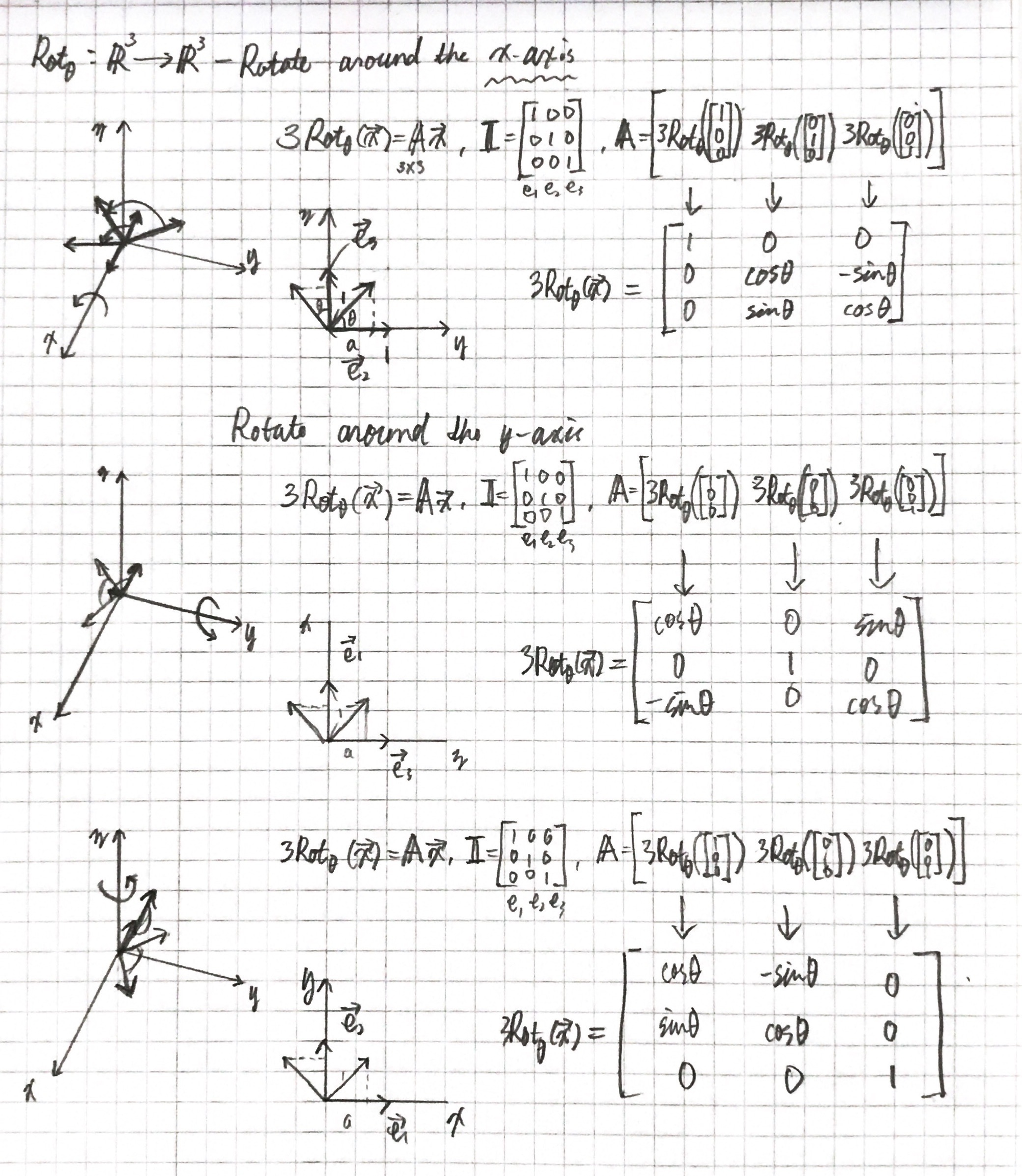
각각의 축에 의한 회전 변환

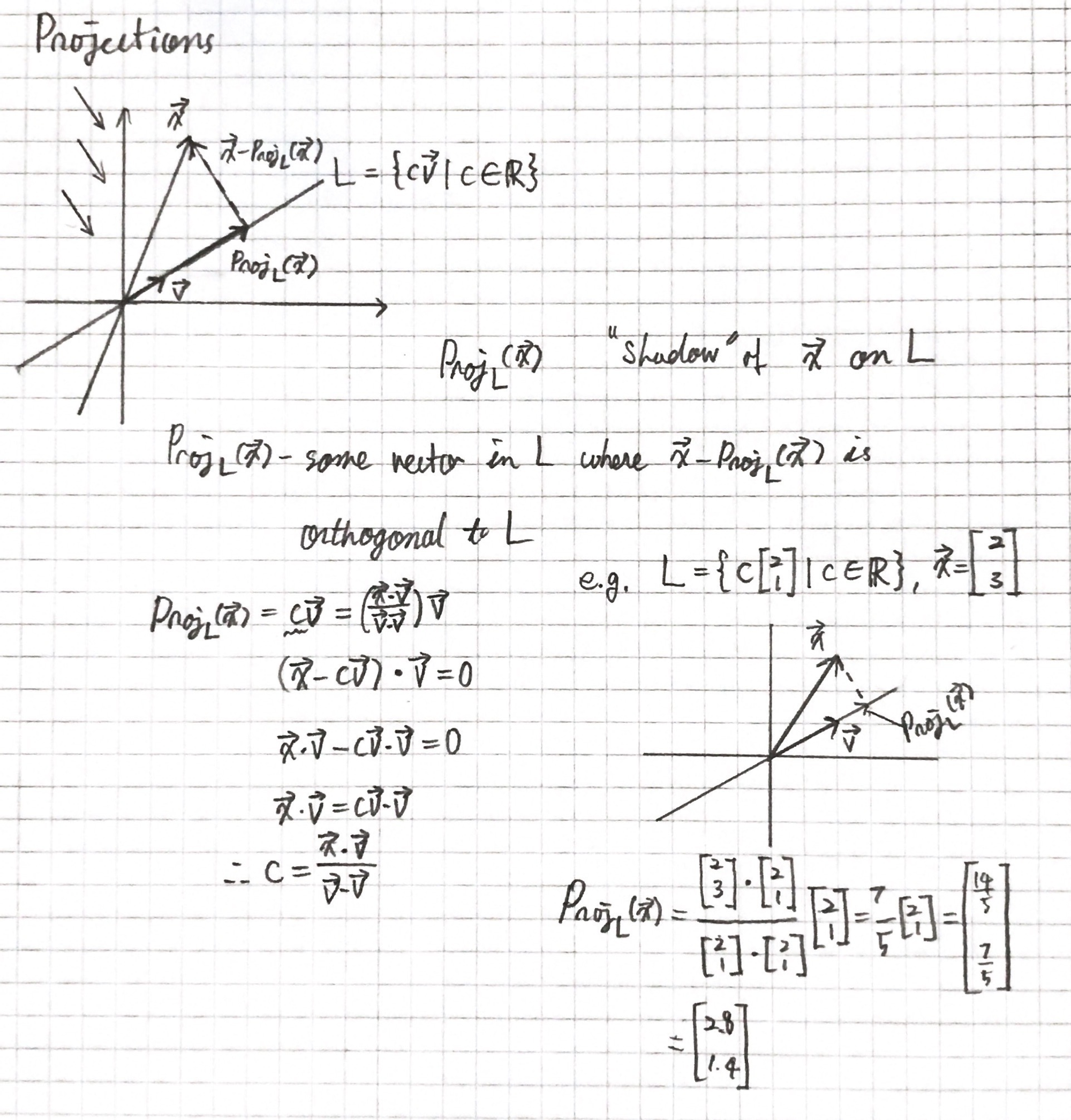
프로젝션(정사영)도 선형성 만족 → 선형 변환

Projection transformation

회전 변환 행렬 유도

Rodrigues' rotation formula

위의 역행렬은 각만 바꾸면 된다. 따라서 row-major일때는 $\vec{v}R_n$ , column-major일 때는 $R_n^T\vec{v}$

위의 변환 행렬은 짐벌락이라는 문제점을 야기시킨다. 자유도 3 → 2로 되는 상황.

Gimbal lock

이 문제점을 예방하기 위해서 사원수(quaternion) 사용하여 회전을 표현해야하는데 이는 더 안전할 뿐만 아니라 컴퓨터 친화적이다. 뒤에서 더 다뤄볼 예정

Combining matrices (Affine Transformation)

여러가지 변환들을 묶어서 사용할 수 있는 것이 변환 행렬 사용의 큰 장점이다.

이제 이러한 수학적 개념을 사용하는데 OpenGL은 행렬과 벡터에 관한 형식을 가지고 있지 않다. 그래서 수학 클래스와 함수를 따로 정의해야한다. 다행히도 OpenGL에 맞춰진, 사용하기 쉬운 수학 라이브러리가 있다.

GLM(OpenGL Mathematics)

GLM은 header-only 라이브러리이다. 이는 헤더만 include만 하면 끝이다. 링킹과 컴파일은 필요하지 않다. glm.g-truc.net/0.9.8/index.html 여기서 다운로드 가능하다. 헤더파일의 루트 디렉토리를 includes 폴더에 복사하여 사용.

Eigen 이라는 C++로 만들어진 선형대수 라이브러리도 있다.

우리가 필요한 GLM의 기능 대부분은 아래의 3가지 헤더에서 다 찾을 수 있다.

#include <glm/glm.hpp>
#include <glm/gtc/matrix_transform.hpp>
#include <glm/gtc/type_ptr.hpp>

한번 테스트 겸 아래와 같이 코드를 작성해보자.

glm::vec4 vec(1.0f, 0.0f, 0.0f, 1.0f);
glm::mat4 trans = glm::mat4(1.0f);
trans = glm::translate(trans, glm::vec3(1.0f, 1.0f, 0.0f));
vec = trans * vec;
std::cout << vec.x << vec.y << vec.z << std::endl;

위 코드를 살펴보면 GLM built-in 클래스를 사용하여 4차원 벡터를 vec으로 생성, 그 다음 4x4행렬을 1.0f만 입력하여 대각선이 다 1.0으로 초기화되는 항등 행렬을 생성한다. 만약 초기화 값 1.0f를 넣지 않으면 요소들 전부 0인 null 행렬이 된다.

다음은 변환 행렬을 생성하는데 glm::translate함수에 항등 행렬을 전달하고 translation 벡터 값도 함께 전달한다. 그리고 벡터와 변환 행렬을 곱하여 결과물을 출력해보면 210이 나온다.

한번 이전에 만들었던 컨테이너 오브젝트를 한번 크기 조정하고 회전해보자.

glm::mat4 trans = glm::mat4(1.0f);
trans = glm::rotate(trans, glm::radians(90.0f), glm::vec3(0.0, 0.0, 1.0));
trans = glm::scale(trans, glm::vec3(0.5, 0.5, 0.5));

먼저 각 축으로 0.5배 만큼 크기 조정하고 z축으로 90도 회전 시킨다. GLM은 그 각을 라디안으로 받기에 glm::radians함수로 변환해준다. 그리고 이전에 만든 오브젝트는 xy 평면에 있으므로 z축을 회전시킨다. 우리가 회전시키는 축은 단위 벡터이여야하는 것을 명심. X 또는 Y나 Z축으로 회전하는게 아니면 normalize하자.

이제 어떻게 shader로 전달할까? shader도 이전 GLSL에서 공부했듯이 mat4 형이 있다. 따라서 uniform 으로 mat4 형 변수를 만들어서 전달하면 된다.

#version 330 core
layout (location = 0) in vec3 aPos;
layout (location = 1) in vec2 aTexCoord;

out vec2 TexCoord;

uniform mat4 transform;

void main()
{
	gl_Position = transform * vec4(aPos, 1.0f);
	TexCoord = vec2(aTexCoord.x, aTexCoord.y);
}

gl_Position에 uniform 변환 행렬을 벡터와 연산하여 전달한다.

unsigned int transformLoc = glGetUniformLocation(ourShader.ID,"transform");
glUniformMatrix4fv(transformLoc, 1, GL_FALSE, glm::value_ptr(trans));

먼저 uniform 변수의 위치를 묻고 그 다음 glUniform에 Matrix4fv를 접미사를 붙여 사용하여 행렬 데이터를 shader로 보낸다.

첫번째 인자는 데이터를 보낼 uniform 변수의 위치, 두번째는 보낼 행렬의 수. 세번째 인자는 행렬을 전치 행렬로 바꾸길 원하는지에 대한 값을 넣어야한다(column과 row를 바꾸는 것). OpenGL 개발자는 종종 내부 행렬 레이아웃을 사용하며, 이는 column-major 형식이고 GLM에서의 디폴트 행렬 레이아웃이다. 따라서 전치할 필요가 없다. 마지막 매개변수에는 실제 행렬의 데이터를 전달하는데 OpenGL의 원하는 방식에 항상 부합하지 않는 방식으로 GLM은 행렬의 데이터를 저장하므로 데이터를 GLM built-in 함수인 glm::value_ptr함수를 사용하여 변환한다.

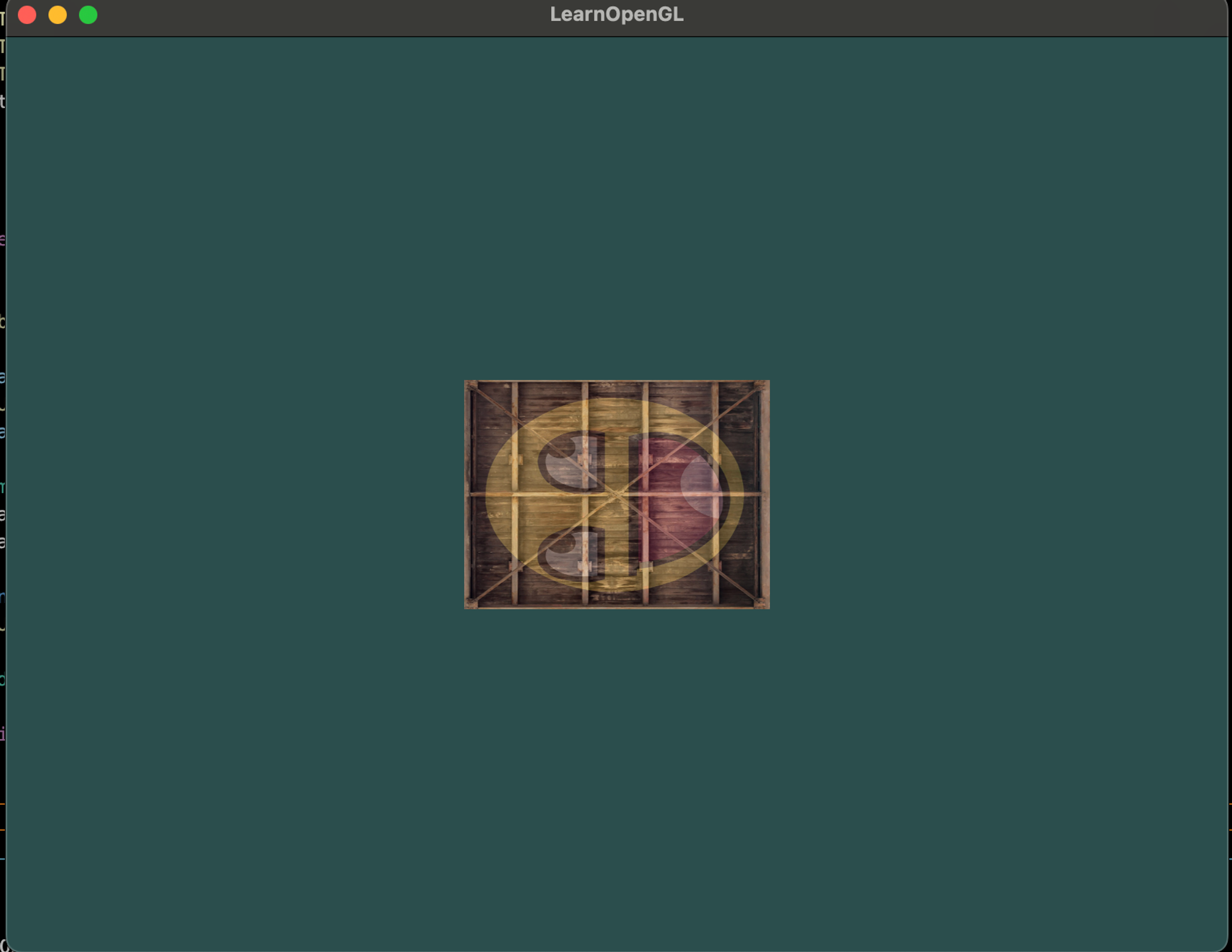
사이즈가 두배 작아지고 z축에서 90도로 회전시킨 결과물이 나온다.

여러가지 테스트를 해볼 수 있다. 다시 오브젝트를 우하단쪽으로 위치시키게 한다. 이 오브젝트를 시간이 지나는 것에 따라 회전시키기 위해서 변환 행렬을 렌더링 루프안에서 업데이트해줘야한다. 왜냐하면 각 프레임마다 업데이트해야하기 때문에.

glm::mat4 trans = glm::mat4(1.0f);
trans = glm::translate(trans, glm::vec3(0.5f, -0.5f, 0.0f));
trans = glm::rotate(trans, (float)glfwGetTime(),
glm::vec3(0.0f, 0.0f, 1.0f));

GLFW의 시간 함수를 사용하여 시간의 변화에 따라 회전각도 변하게 한다. 이전 경우에는 변환 행렬을 어디든 선언할 수 있었지만 이같은 경우에는 변환 행렬을 렌더 루프안에서 다시 생성해야한다. 보통 렌더링할 때 각 프레임에 대한 새로운 값을 가지고 재생성된 여러가지 변환 행렬을 가진다.

여기서 처음에 컨테이너 오브젝트를 원점에서 회전시키고 회전된 버전을 우하단으로 이동시킨다. 실제 변환 순서는 반대인 것을 기억하자. 비록 코드에서는 이동시키고 회전하지만 실제 변환은 회전을 먼저 적용하고 이동시킨다. 이러한 모든 복합 변환들의 조합들을 이해하는 것과 어떻게 오브젝트들에 적용되는지 이해하기 어렵다.

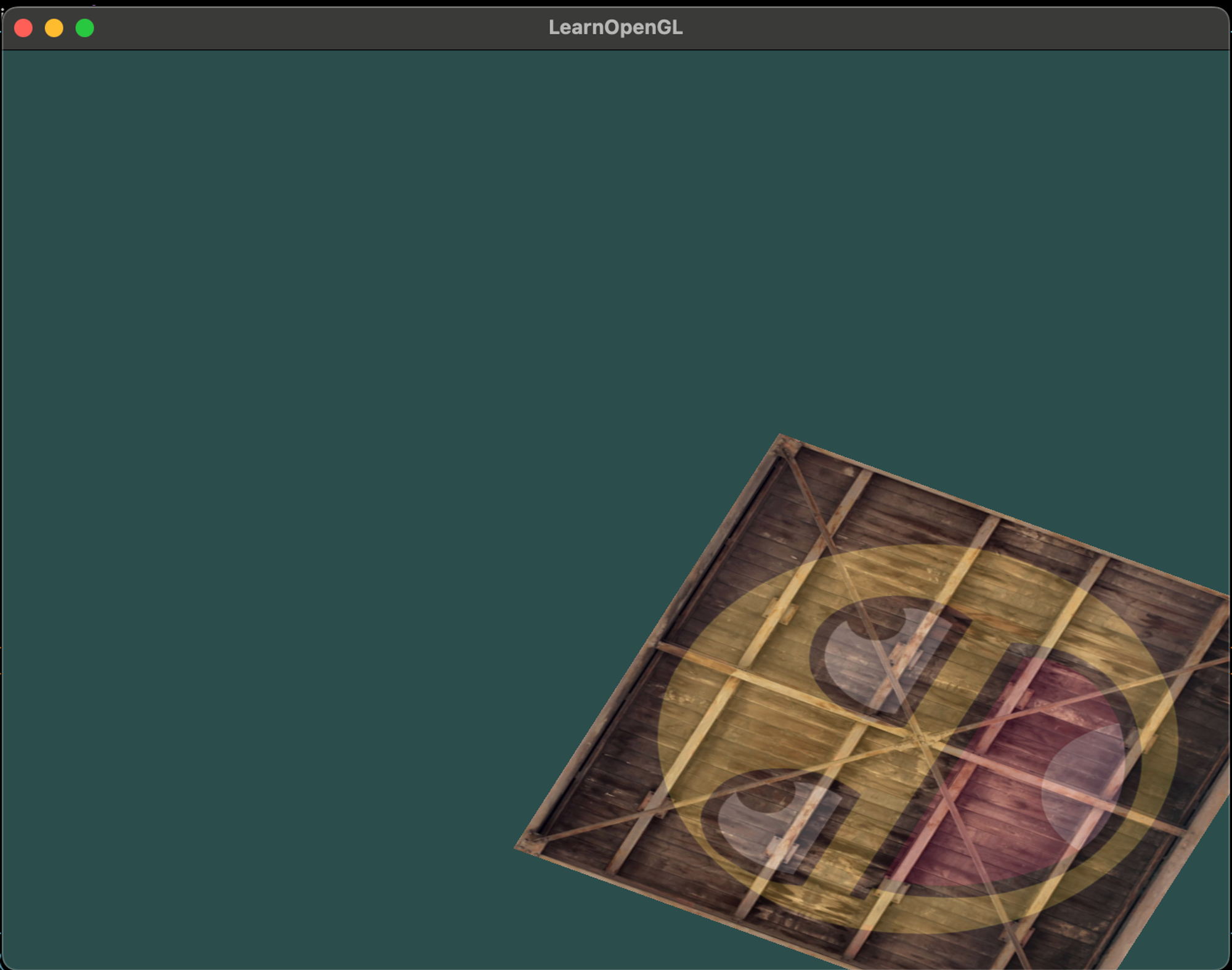
위와 같이 우하단에서 계속 회전하는 결과물을 얻을 수 있다. 이동과 회전을 하나의 행렬로 했다. 이는 그래픽스에서 매우 중요한 부분이다. 무한히 많은 양의 변환을 정의할 수 있고 이것들을 원하는 만큼 재사용할 수 있게 하나의 행렬로 결합할 수 있다. 이같은 변환을 vertex shader에서 사용하는 것은 vertex 데이터들을 다시 재정의하는 수고를 덜 수 있으며 처리하는 시간 또한 절약한다. 매번 데이터를 다시 보낼 필요가 없기 때문이다. 해야할 일은 변환 uniform을 업데이트하는 것이다.