알고리즘
1.허프만 인코딩
고정길이코드 VS 가변길이코드 > 고정길이코드는 각 문자당 비트 수(code word의 길이)가 정해져있기 때문에 인코딩, 디코딩 시 분석이 쉽다. 가변길이코드는 각 분자당 비트 수(code word의 길이)가 다르기 때문에 인코딩, 디코딩 시 분석이 어렵다. BUT,
2.그리디 알고리즘2(Greedy Algorithm)

그리디 알고리즘? > 그리디 알고리즘은 현재 주어진 상황에서 할 수 있는 최선의 선택하는 알고리즘이다. 물론 현재 상황의 최적의 해가 전체 문제의 최적의 해가 되는 것은 보장할 수 없다. 그러므로, 그리디 알고리즘은 한정된 문제에서만 사용할 수 있다. 각 선택에서 전의
3.완전탐색(Brute-Force) 기법

완전탐색? > Brute(단순히,순전히)Force(힘): 순전히 힘으로 밀어붙이는 문제 해결 기법. 컴퓨터의 빠른 계산 능력을 사용하여 모든 경우의 수를 다 계산하는 것을 의미한다. ex) 4자리 비밀번호 풀기 -> 0000~9999까지 모두 대입해본다. *효율성 완
4.DFS / BFS

DFS / BFS 유형 > DFS, BFS는 가능한 모든 경우의 수를 체크해서 정답을 찾는 Brute-Froce(완전탐색) 문제를 해결할 수 있는 알고리즘이다. DFS, BFS를 사용해야 하는 문제 유형으로, 1. A지점에서 B지점까지 도달하는데 걸리는 최단경로(시간)
5.DP(다이나믹 프로그래밍)

어떤 문제를 작은 문제(subproblem)들로 쪼개고, 작은 문제들을 해결하여 그 답을 이용해 큰 문제를 해결하는 알고리즘으로, 중복되는 subproblem의 답을 저장(memoization)해두어 재활용 함으로써 효율성을 높이며 문제를 해결하는 테크닉이다.문제를 s
6.최장 증가 부분 수열(LIS)
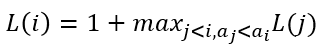
LIS(Longest Increasing Subsequence)? > 최장 증가 부분 수열이란, 원소가 n개인 수열의 부분수열 중 각 원소가 이전 원소보다 크면서 그 길이가 최대인 수열이다. ex)
7.[알고리즘 유형 / 접근법] 이분탐색
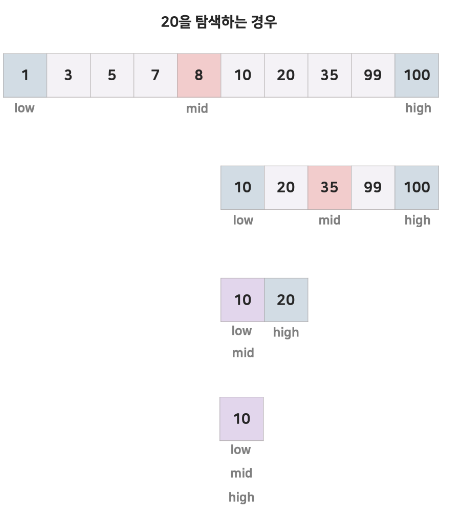
정렬된 배열에서 어떠한 값을 빠르게 찾을 때 사용할 수 있는 알고리즘이다. 배열의 양 끝을 가리키는 인덱스를 left = 0, right = N - 1로 설정하고 mid = (left + right) / 2로 설정한 후, 인덱스 mid에 해당하는 값과 찾는 값을 비교하
8.[알고리즘 유형 / 접근법] 코드 구현력

> 뇌지컬로 최대한 풀면 되는데, 몇가지 스킬을 쓸 수 있음. 배열 선언해서 값 저장 > 출처 : 인프런 파이썬 알고리즘 문제풀이 입문 (코딩테스트 대비) 강의 풀이 > 정4면체 : 1,2,3,4 / 정6면체 : 1,2,3,4,5,6 나올 수 있는 두 눈의 합 중
9.[알고리즘 유형 / 접근법] 그리디 알고리즘

어떤 문제를 푸는 단계에서 선택의 순간마다 당장의 최적을 선택하여 최종 문제의 최적의 해를 찾아내는 알고리즘이다. 보통의 그리디 문제는 정렬을 수행한 후 문제를 풀면 된다. Local Optimal Solution = Global Optimal Solution 전 단계
10.[알고리즘 유형 / 접근법] 투 포인터
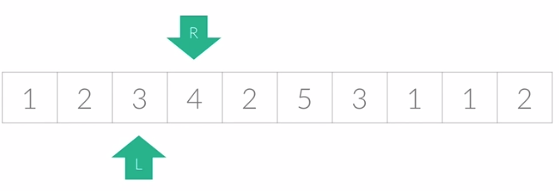
C에서 포인터라는 개념이 있다. 어떤 변수의 주소를 값으로 갖는 변수인데, 알고리즘에서 이와 비슷한 개념을 활용하여 문제를 해결할 수 있다. 배열, 리스트 같은 순차 자료구조에서 특정 범위를 탐색하거나, 부분 수열(문자열) 등을 찾는 문제에서 사용할 수 있다. 위와 같
11.[알고리즘] 유니온 파인드 알고리즘 (union-find)

위와 같은 그림에서 연결된 그래프의 집합을 찾아내는 알고리즘이다. 1은 7과 연결돼있고, 7은 6과 연결돼 있을 때, 1과 6이 연결됨을 쉽게 찾아낼 수 있는 알고리즘이다. 해당 알고리즘에는 두 가지 핵심 동작이 있다. union : 서로 다른 두 개의 집합을 하나의
12.[알고리즘] 최소 신장 트리 MST

무방향 그래프에서 간선의 비용을 최소로 하는 사이클이 없는 트리이다. N개의 정점을 연결하는 N-1개의 간선을 선택한다. MST를 구하는 알고리즘에는 크루스칼(Kruskal) 알고리즘, 프림(Prim) 알고리즘이 있다.크루스칼 알고리즘은 간선을 중심으로 MST를 구하는
13.[알고리즘] java 문자열 스킬
public String substring (int startIndex, int endIndex) //endIndex는 불포함public String split (String regex)public String split (String regex, int limit)
14.[알고리즘] 그래프 사이클
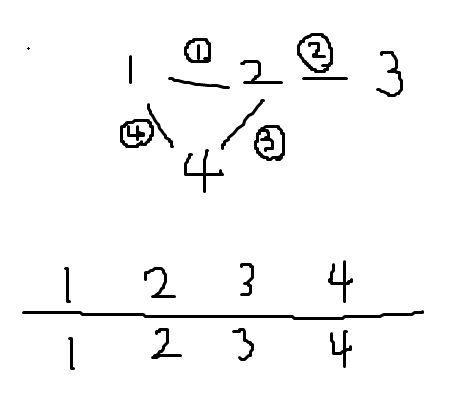
그래프에서 사이클을 판별하는 방법 정리union-find 알고리즘을 사용할 수 있다. 초기 상태이다. 1번 간선을 탐색한다. 2번 간선을 탐색한다.3번 간선을 탐색한다. 4번 간선을 탐색할 때, 1과 4의 parent 배열 값이 같기 때문에, 사이클이 존재한다고 판단할
15.[알고리즘] 위상정렬
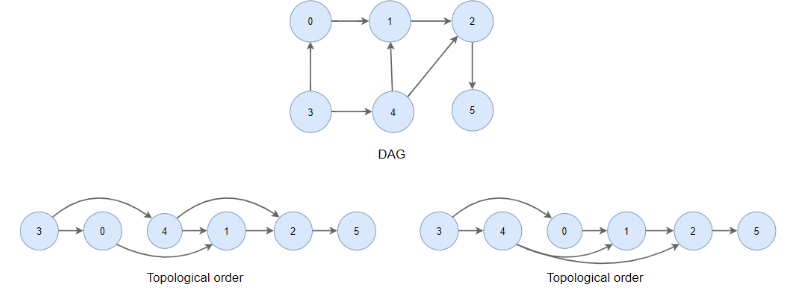
위상정렬은 순서가 정해진 작업을 처리할 때, 그 순서를 정하기 위해 사용하는 알고리즘이다. 사이클이 없는 방향 그래프(DAG)에서 노드의 순서를 구할 수 있다. 물론 정렬 결과는 여러개가 될 수 있다. 생각해보면 당연하지만 주의할 점은 그래프에 사이클이 있으면 안된다는