최장 증가 부분 수열(LIS)

LIS(Longest Increasing Subsequence)?

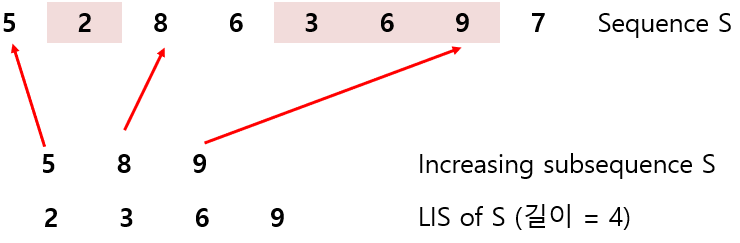
최장 증가 부분 수열이란, 원소가 n개인 수열의 부분수열 중 각 원소가 이전 원소보다 크면서 그 길이가 최대인 수열이다.
ex)

DP를 이용한 LIS 구하기

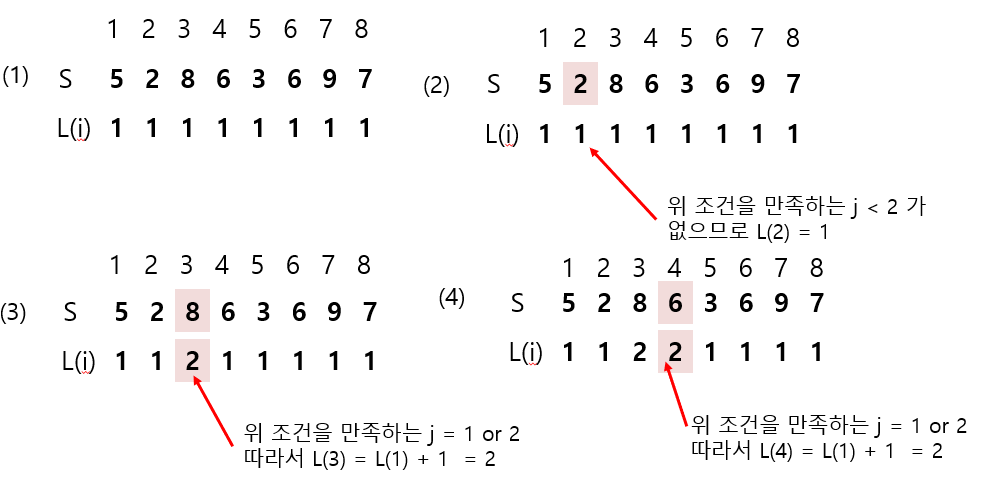
1. LIS의 길이를 저장할 dp배열(길이는 수열의 길이와 같음)을 하나 선언한다. (1로 초기화)
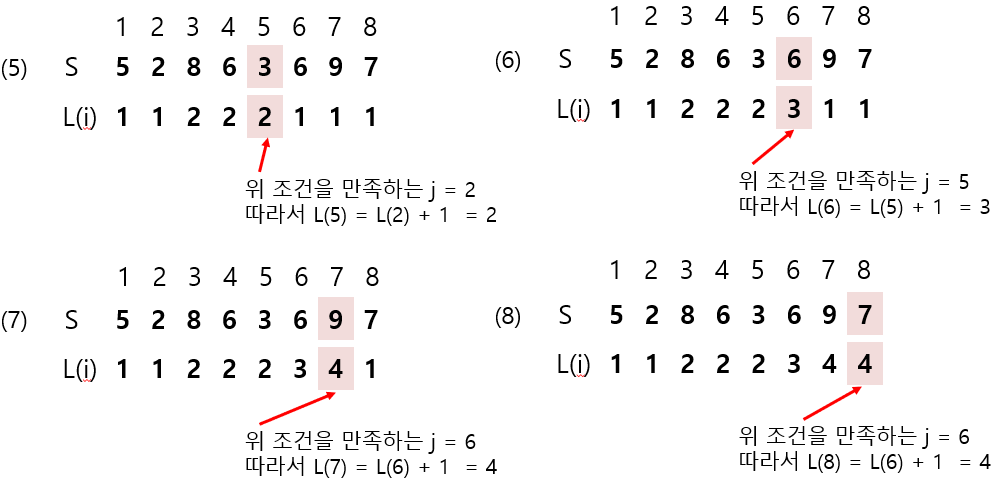
2. 수열을 처음부터 탐색하면서 현재 탐색중인 원소보다 작으면서, dp배열의 값이 가장 큰 원소의 dp배열 값을 더해 dp배열에 넣는다. (dp배열의 값 == 길이)
   식으로 나타내면 위와 같다.
3. 2를 수열의 끝까지 반복한다.

• 뭔소린지 모르겠지? 그림을 보자 (S는 수열, L은 dp배열
  
  
  
  위의 예시에서 S의 LIS의 길이는 4이고, 2367, 2368 두개가 있다.
  시간복잡도: O(n^2)

+다른 방법

lower bound(?)를 이용하는 방법도 있다고 하는데, 그 방법은 시간복잡도가 O(nlogn)이라고 한다.
나중에 공부해보기

관련 백준 문제

11053