개념
어떤 문제를 작은 문제(subproblem)들로 쪼개고, 작은 문제들을 해결하여 그 답을 이용해 큰 문제를 해결하는 알고리즘으로, 중복되는 subproblem의 답을 저장(memoization)해두어 재활용 함으로써 효율성을 높이며 문제를 해결하는 테크닉이다.
방법
- 문제를 subproblem으로 쪼갤 수 있는지 확인
- subproblem간의 재귀적 관계 파악(중복 파악)
- n차원 배열을 통해 subproblem의 값 저장
ex)피보나치 수열
피보나치 수열은 DP의 대표적인 예이다.
f(n) = f(n-1) + f(n-2)
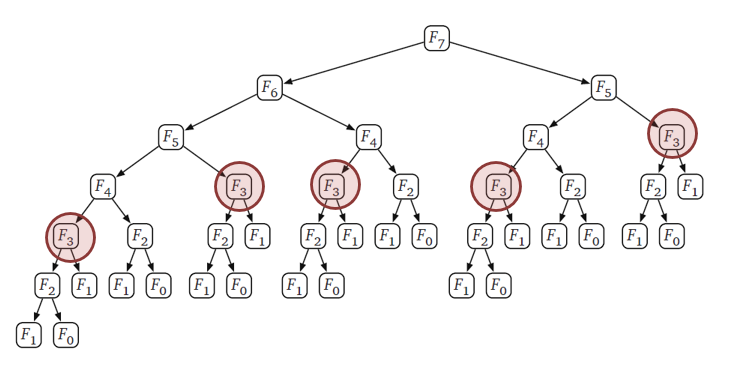
위의 그림에서 보면, DP를 사용하지 않고 f(n)을 구하려 하면 시간복잡도는 O(2^n)이 된다.
여기서 f5,4,3,2는 중복되어 계산됨을 알 수 있는데, 이 부분을 memoization을 이용하여 개선할 수 있다.
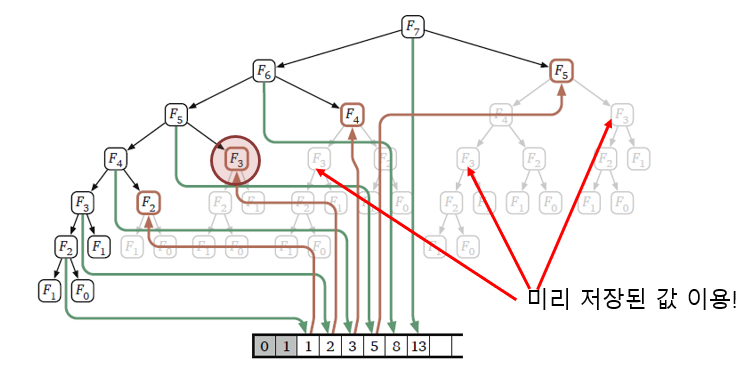
위와 같이 중복되는 부분들을 배열에 저장해두고 사용하면, 시간복잡도는 O(n)으로 줄어들게 된다.
**recursion과 memoization을 사용하여 알고리즘을 설계하는 테크닉이 DP!!**
피보나치 코드
#include <iostream>
using namespace std;
int memo[100] = { 0, }; //memoization을 위한 배열
int fib(int n) {
if (n == 1) return 1; //1
if (n == 2) return 1; //fib(0) + fib(1) = 0 + 1 = 1
//만약 n의 값이 이전에 구한 값이라 memo배열에 저장되어 있다면 그 저장된 값 리턴.
if (memo[n] != 0) return memo[n];
return memo[n] = fib(n - 1) + fib(n - 2); //계산값을 memoization
}
int main(void) {
cout << fib(10); //55
return 0;
}대표적이 DP문제(하나씩 포스팅 할 것)
- Longest Increasing Subsequence (LIS)
- Minimum Edit Distance (최소 편집 거리)
- single-source shortest path problem - 다익스트라, 벨먼-포드 알고리즘
- all-pairs shortest path problem - 플로이드-워셜 알고리즘
- Optimal Binart Search Tree