로지스틱 회귀

로지스틱 회귀 모델은 시그모이드 함수를 사용하여 데이터를 설명하는 최적의 선으로 답을 찾는 알고리즘이다.
로지스틱 회귀는 분류에 주로 사용되는 알고리즘이다.

로지스틱 회귀의 산식

$S(x) = \frac{1}{1+e^{-x}} = \frac{e^{x}}{e^{x}+1}$

시그모이드 함수 만들기

#시그모이드 함수 만들기
import numpy as np
import matplotlib.pyplot as plt

#시그모이드 함수 정의하기
def sigmoid(x):
  #numpy.exp() 함수는 밑이 자연상수 e인 지수함수(e^x)로 변환
  return 1 / (1 + np.exp(-x))

#함수 테스트용 데이터 생성하기
#test = np.array([-1,0,1])

#print(sigmoid(test))
#시그모이드 함수 그래프 그리기
#그래프 적용 위한 데이터 만들기
sigmoid_x = range(-6,7)
# 시그모이드 함수를 적용한 값
sigmoid_y = sigmoid(np.array(sigmoid_x))
# 선 그래프 그리기
plt.plot(sigmoid_x, sigmoid_y, color = 'blue', linewidth = 0.5)
#백그라운드에 모눈종이 설정
plt.rcParams['axes.grid'] = True

#선 굵기 설정
plt.axvline(x =0, color= 'black', linewidth =3)
plt.yticks([0,0.5,1])
plt.show()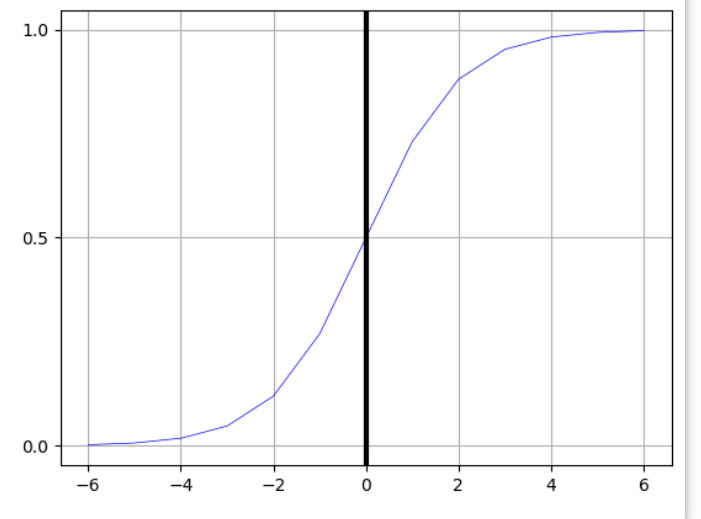

위와 같이 -6 ~ 6사이의 정수를 배열로 생성하여 시그모이드 함수의 수식을 활용해 데이터를 0에서 1 사이의 수로 변환시켜주었다.

로지스틱 회귀 실습

로지스틱은 앞서 설명한바와 같이 분류를 위한 모델로 많이 사용된다고 하였다. 특정 수의 집합을 0에서 1 사이의 수로 분류하여 컴퓨터가 이해하기 쉬운 수로 변환된다.
다음 실습 자료는 학습 데이터를 생성하고 추론 데이터를 이용하여 학습된 로지스틱 함수가 학습데이터를 분류시키는 모습을 볼 수 있다.

# 학습 데이터 생성하기
x_train = [3,4,5,6,7,8,9,10,11,12,13,14,15,16,17]
y_train = [0,0,0,0,0,0,0,1,1,1,1,1,1,1,1]

# 추론을 위한 데이터 생성하기
x_test= [0,1,2,18,19]
y_test= [0,0,0,1,1]

#학습 데이터에 대해 numpy로 변경 및 행을 열로 변경하기
x_train = np.array(x_train).reshape([-1,1])
y_train = np.array(y_train)

# 로지스틱 회귀 학습하기

#라이브러리 불러오기
from sklearn.linear_model import LogisticRegression
#생성
logi_reg = LogisticRegression()
#학습
logi_reg.fit(x_train, y_train)
#역산을 위한 기울기 절편 여부 확인
print('intercept : ', logi_reg.intercept_)
print('coef : ', logi_reg.coef_)

#기울기와 절편을 수동으로 결과 만들기
odd =[]
for i in x_train :
  odd.append((logi_reg.coef_*i)+logi_reg.intercept_)
sigmoid_y = sigmoid(np.array(odd))
sigmoid_y = sigmoid_y.reshape(-1,1)

#역산된 그래프 표시하기
plt.scatter(x_train, y_train, color='red')
plt.plot(np.array(x_train), sigmoid_y, color='blue')
plt.yticks([0,0.5,1])
#y축의 범위 : [Ymin, Ymax]
plt.ylim([-0.1,1.1])
plt.show()

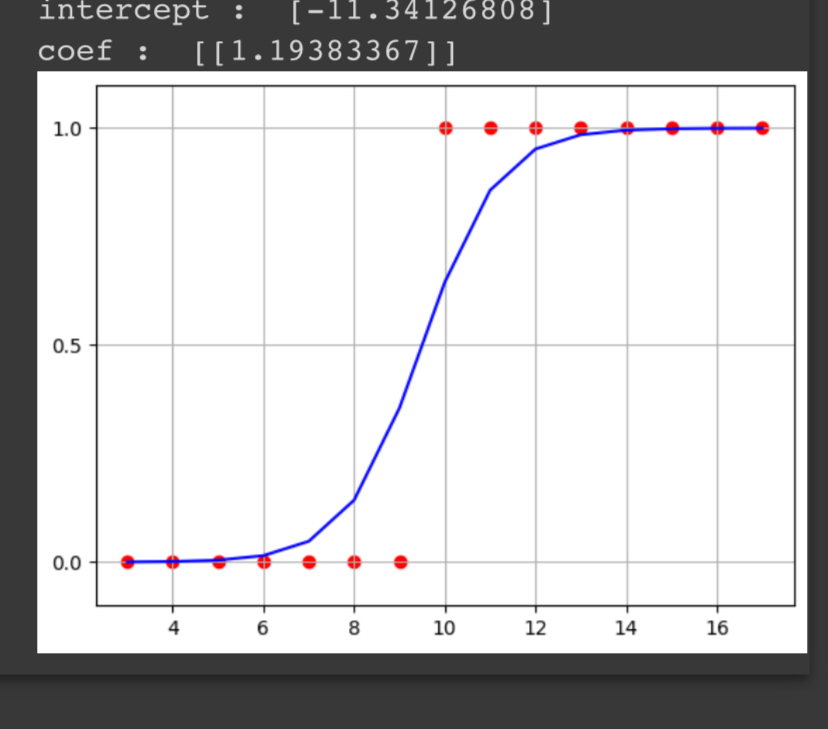
위 그래프와 같이 10 이상인 수를 1로 분류하고 이하인 수를 0으로 분류하는 모습을 볼 수 있다.
이처럼 로지스틱 회귀는 시그모이드 함수를 이용하여 데이터를 0 또는 1로 분류하는 모델이다.