[Open DMQA Seminar] Unsupervised Domain Adaptation in Regression 리뷰

[Video Label]

Intro

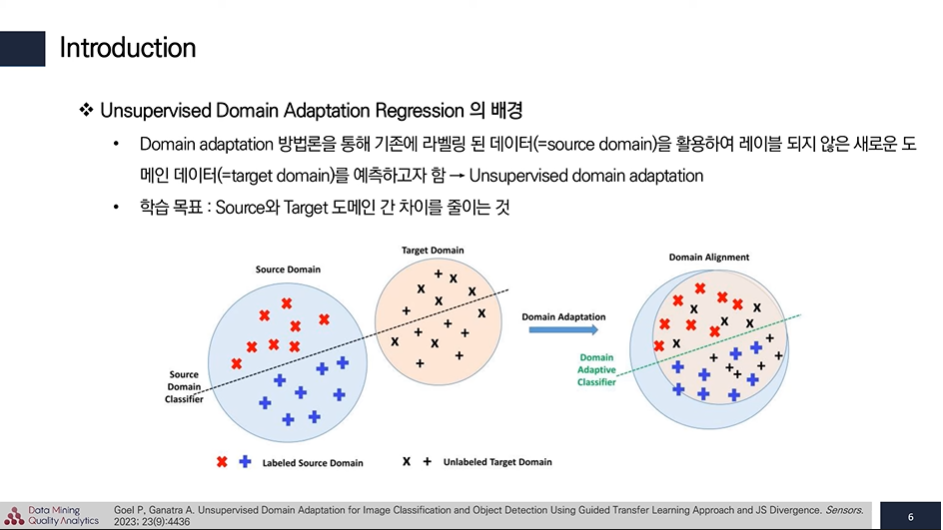
label 데이터 부족 현상을 해결하기 위해 Unsupervised Domain Adaptation을 활용해 레이블 되지 않은 새로운 도메인 데이터를 예측하는 방법을 사용한다.

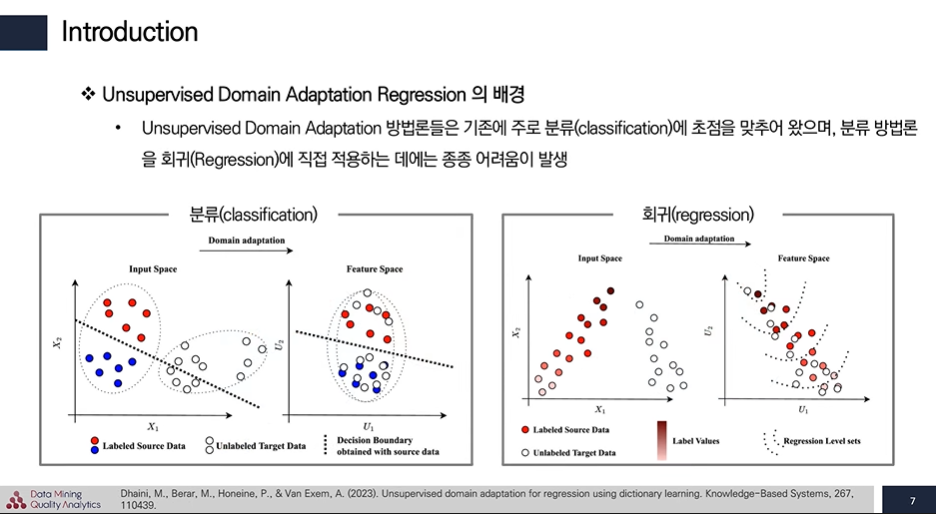
기존 Domain adaptation을 분류 문제에 초점 되어 왔다. 이러한 분류 문제를 풀때에 Domain adaptation을 회귀 문제에 적용할 때 어려움을 겪는다.

Representation Subspace Distance for Domain Adaptation Regression (ICML, 2021)

Method

• Regression의 대표 손실 함수 = MSE
• Classification의 대표 손실 함수 =Cross Entropy loss
  

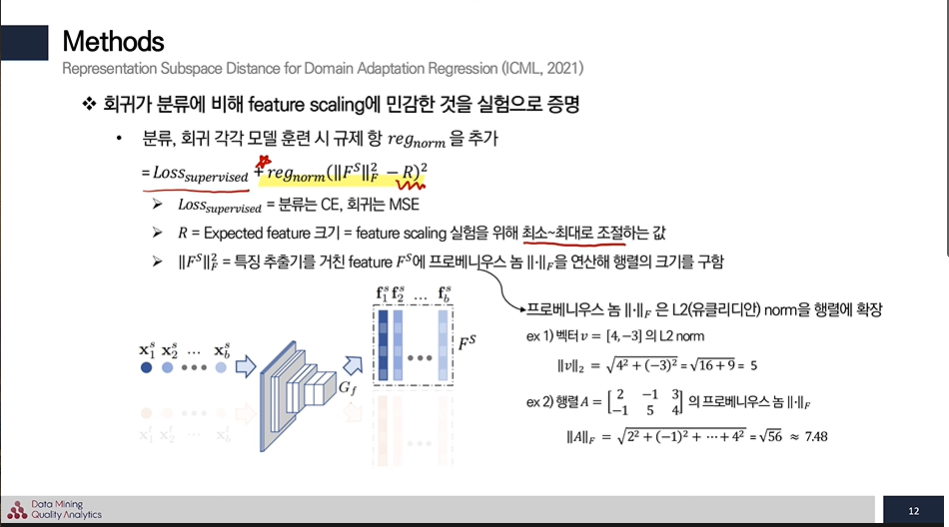
이에 R을 우리가 예측하는 Feature의 크기이고
프로베니우스 놈은 실제 Feature의 크기를 뜻한다.

따라서 회귀가 분류에 비해 feature scaling에 민감한 것을 실험으로 증명하기 위해 feature 크기를 통제해서 동일한 조건에서 R이 변할 때 얼마나 값이 민감하게 반응하는지를 살펴보기 위한 규제값이다.

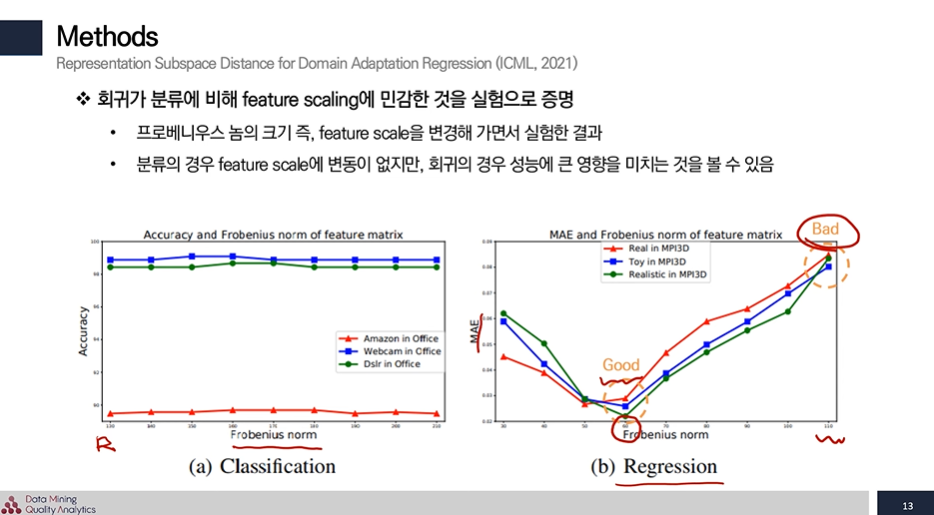
결과로 Classification은 결과에 큰 변화가 없지만, Regression은 feature 크기에 따라 성능이 크게 바뀌는 것을 볼 수 있었다.

모델 훈련 방법

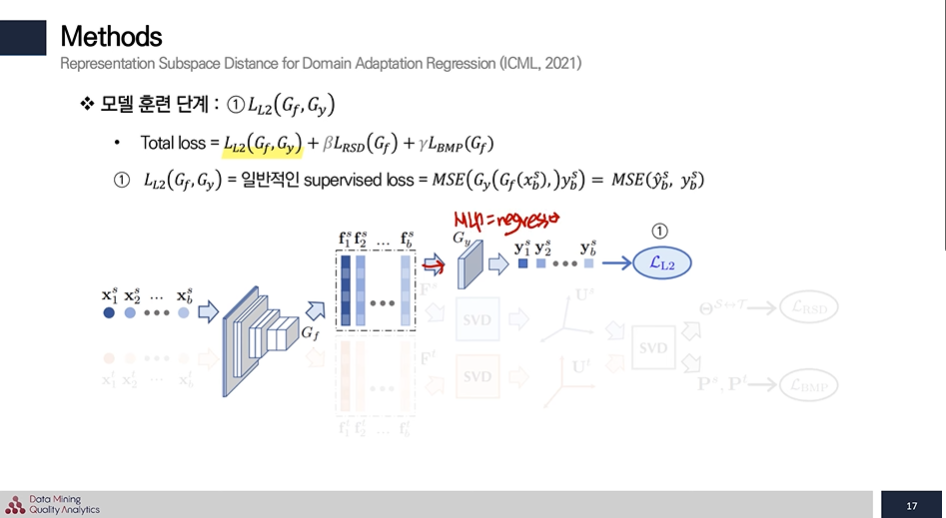
• 1번 : Loss식은 회귀에서 일반적으로 쓰이는 supervised loss로 사용된다.

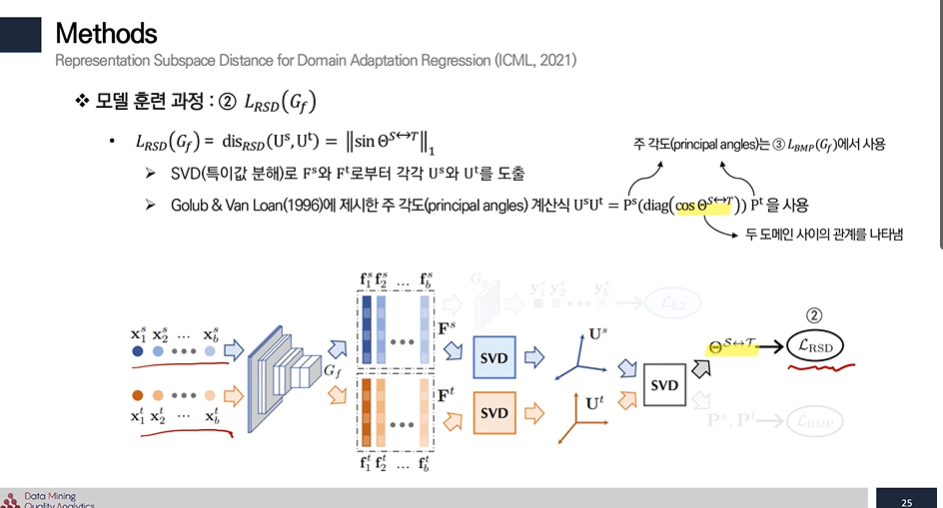
• 2번 : Source 와 Target SVD(특이값 분해 U열) 차 → 두 도메인간 차이를 Loss로 두어 유사해지게!

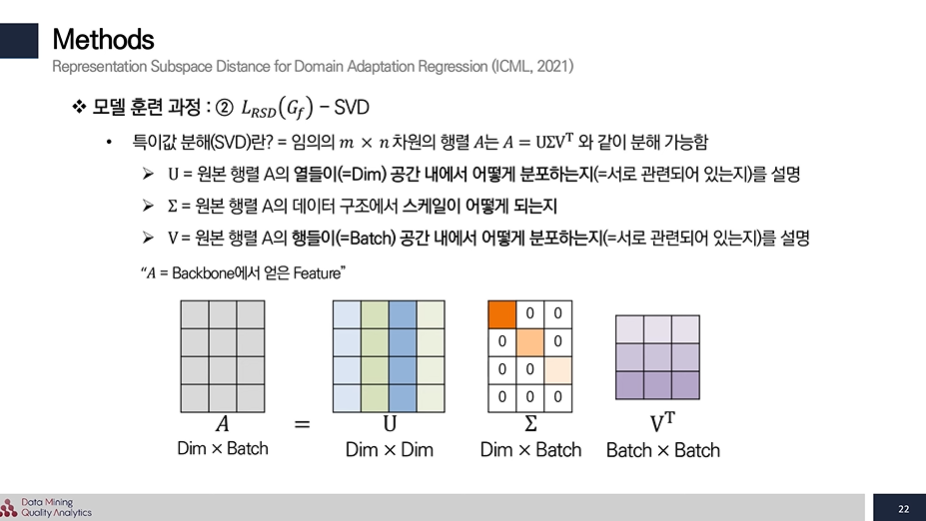
특이값 분해
특이값 분해는 mxn 차원 문제를 3가지 방식으로 나눌 수 있는데 이는 차원 축소 및 특성 유지를 가능케 한다.

(3가지 방식

• 열 기반 직교 행렬: 원본 행렬 A의 열들이 공간 내에서 어떻게 분포하는지를 설명
• 대각 행렬 (벡터의 길이를 조절하는 특이 값, feature scale에 영향을 준다.) : 원본 행렬 A의 데이터 구조에서 스케일이 어떻게 되는지
• 행 기반 직교 행렬 : 원본 행렬 A의 행들이 공간 내에서 어떻게 분포하는지를 설명

)

이중 U열 (열 기반 직교 행렬)만 사용하는데 그 이유는

리만 기하학 이론을 기반으로 U는 원본 행렬 A의 방향을 나타내며, 스케일과 독립적, U를 통해 원본 행렬 A의 구조적 형태를 충분히 특정할 수 있기 때문이라고 한다.

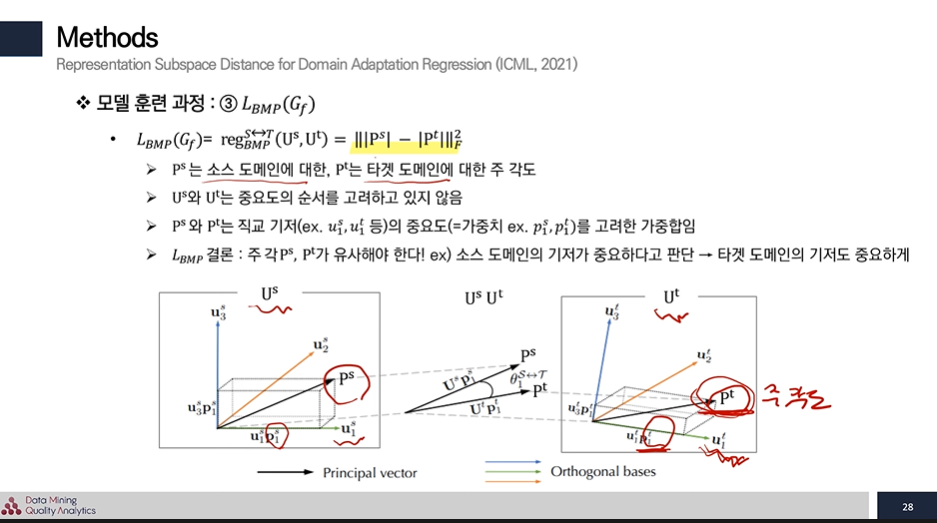
3번 : Source 와 Target의 기저 차 → Source와 Target의 서브스페이스 기저를 추출해서 소스 도메인에서 중요하다고 생각하는 방향을 target에서도 중요하게 하는 Loss다.

따라서 실험을 통해 확인한 결과 feature scale에 민감한 회귀 문제를 SVD를 통해 새로운 거리를 정의하여 차이를 줄이 되 feature scale은 유지하면 좋은 성능을 달성 했다.

DARE-GRAM: Unsupervised domain adaptation regression by aligning inverse gram matrices. (IEEE/CVF)

Method

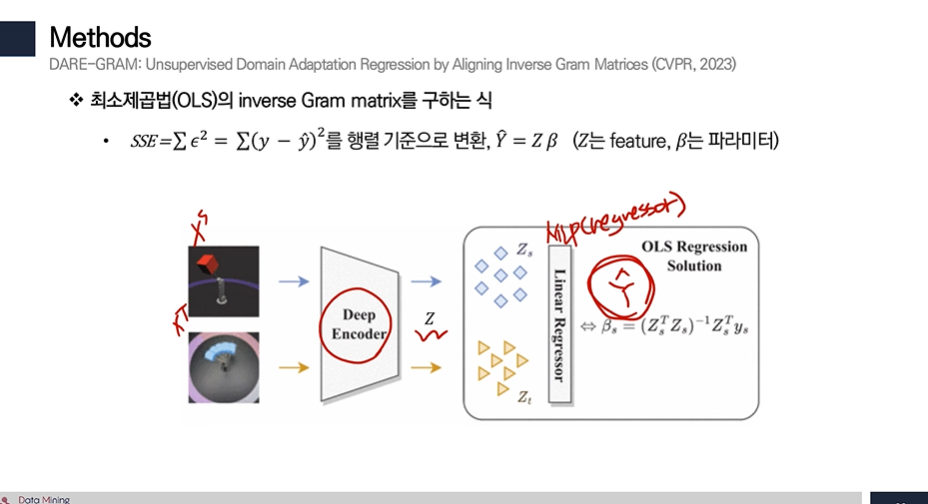
최소제곱법 (OLS)에서 inverse Gram matrix를 구해서 사용해야 한다고 하는데 이를 보여주기 위한 증명이 다음에서 나온다.

• 실제 값 Y와 가장 가깝게 되도록 b를 구한다.
• 따라서 SSE를 최소화하는 b를 찾아야 하며,
  최솟값을 찾기 위해 미분해서 0이 되는 지점을 찾게 되면 다음과 같다.
• 미분한 값에서 결국 역행렬이 나오게 되며, 이는 회귀 task에서 역행렬을 사용하는 것이 올바를 것이라는 근거가 된다.

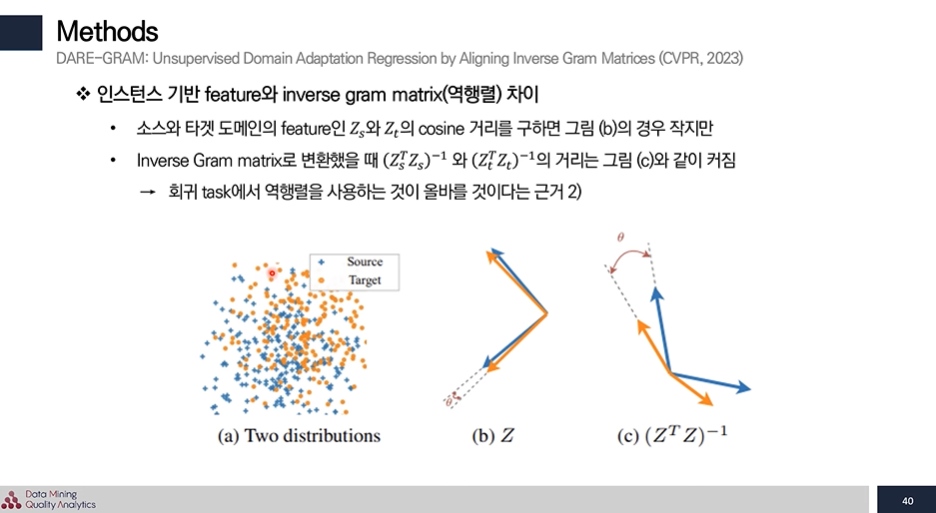
이를 실제로 적용해 보면 cosine 거리를 구하면 Z로 봤을 때는 거리가 가까워 보이지만 역행렬로 구하면 실제로 거리가 멀어 역행렬로 구하는 것 올바를 것이라는 근거를 보여준다.

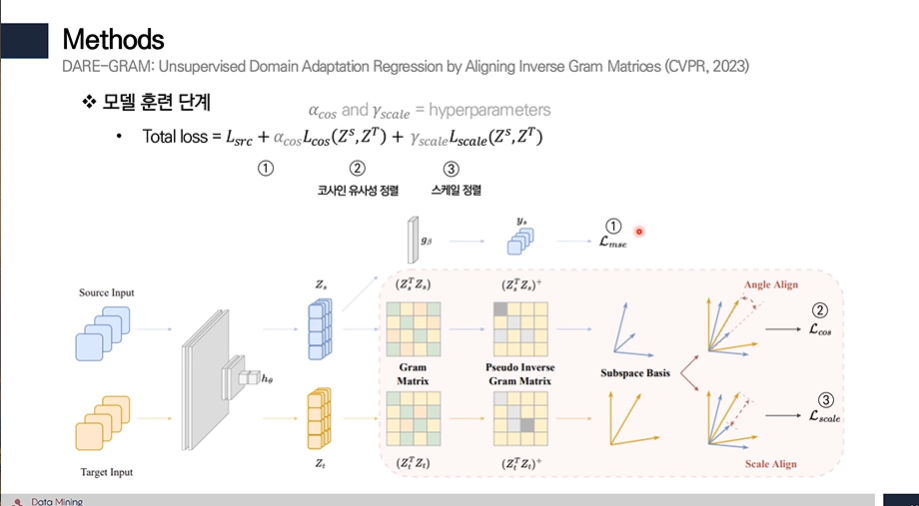
1번 : 일반적인 supervised loss → MSE 값

2번 :

• 이번에는 벡터의 길이를 조절하는 diagonal matrix를 추출하여 특이 값을 추출하고,
• 이를 이절 threshold 이상의 분산을 가진 특이 값 만을 선택하여 유사 역행렬을 도출한다.
• source 와 target의 유사 역행렬로부터 코사인 유사도를 계산해 angle이 같고, 이상적인 유사도인 1이 되게 정렬을 한다.

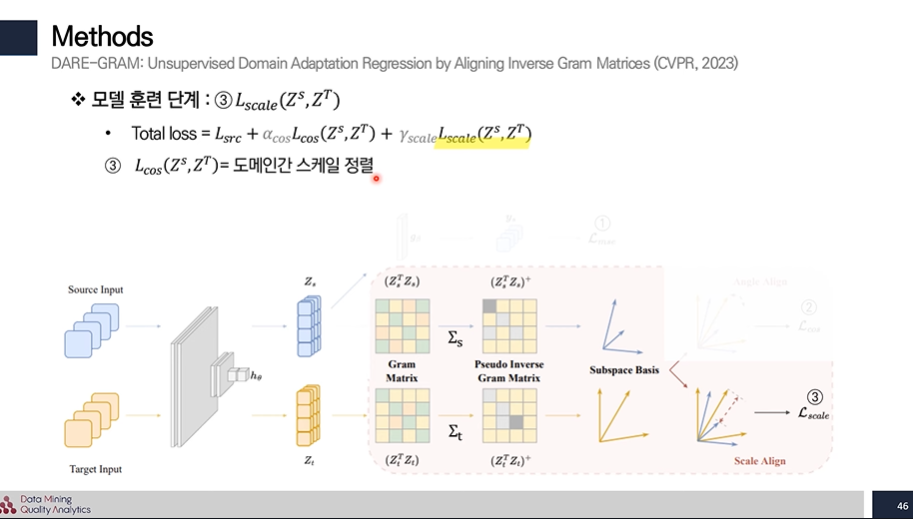
3번 :
아까 구한 특이 값의 차를 L2 norm으로 계산하여 스케일을 일치 시켜준다.