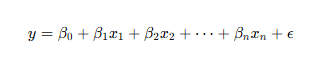1. 통계적 회귀 모델

1-1. 기본 개념

회귀(Regression)란?
회귀 분석은 한 변수(종속 변수)가 다른 변수들(독립 변수)에 의해 어떻게 설명되는지를 알아보기 위한 통계적 방법입니다.
예) 광고비(독립 변수)가 매출(종속 변수)에 미치는 영향을 분석

독립 변수(설명 변수): 결과에 영향을 줄 것으로 예상되는 변수

종속 변수(반응 변수): 예측하고자 하는 결과 값

1-2. 선형 회귀 (Linear Regression)

모델의 가정

선형 관계 : 독립 변수와 종속 변수 간에 직선(선형) 관계가 있다고 가정

오차항의 정규성 : 실제 값과 예측 값의 차이가 정규분포를 따른다고 가정

최소제곱법(OLS: Ordinary Least Squares)

• 관측된 데이터와 예측된 값 사이의 오차 제곱합을 최소화하는 방식으로 계수를 찾습니다.

1-3. 로지스틱 회귀 (Logistic Regression)

• 사용 목적:
  결과가 이진형(예: 성공/실패, 낙찰/비낙찰)일 때 확률을 예측

• 모델의 수학적 표현:
  선형 회귀와 비슷하지만, 출력 값을 0과 1 사이의 확률로 변환하기 위해 시그모이드 함수를 사용합니다.

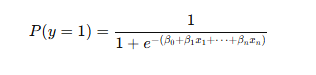
개념 설명:
시그모이드 함수는 입력값이 아주 작으면 0, 아주 크면 1에 가까워지는 S자 모양의 함수입니다.

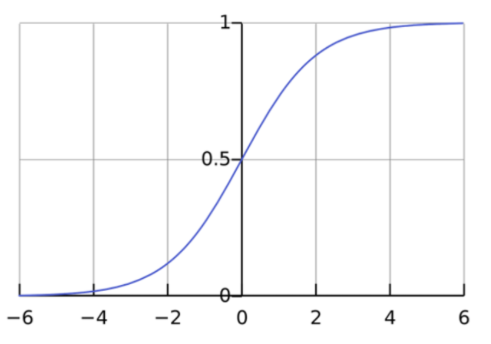
출처 : https://aws.amazon.com/ko/what-is/logistic-regression/

---

2. 머신러닝 모델

2-1. 머신러닝의 기본 개념

• 정의:
  데이터에서 패턴이나 규칙을 학습하여 새로운 데이터에 대해 예측하거나 분류하는 알고리즘과 기술의 집합입니다.

<학습 유형>

지도 학습(Supervised Learning): 입력과 출력 데이터가 모두 주어지고, 모델이 이 관계를 학습

비지도 학습(Unsupervised Learning): 데이터만 주어지고, 데이터 내의 구조나 패턴을 찾음

강화 학습(Reinforcement Learning): 환경과 상호작용하며 보상을 극대화하는 행동을 학습

2-2. 주요 알고리즘과 개념

랜덤 포레스트(Random Forest)

개념: 여러 개의 결정 트리(Decision Tree)를 만들어 투표나 평균을 통해 예측

장점: 과적합(overfitting)을 줄이고, 다양한 데이터 패턴을 잡아내는 강력한 앙상블 기법

XGBoost

개념: Gradient Boosting 알고리즘의 한 종류로, 여러 약한 예측기를 순차적으로 결합하여 강력한 예측 모델을 만듦

특징: 빠른 계산 속도와 높은 예측 성능

신경망(Neural Networks)

구조: 입력층, 은닉층, 출력층으로 구성된 네트워크

활성화 함수(Activation Function): 비선형 변환(예: ReLU, sigmoid)을 통해 복잡한 패턴을 학습

학습 방법: 역전파(Backpropagation) 알고리즘을 사용하여 가중치를 업데이트

2-3. 추가 개념

과적합(Overfitting)과 일반화(Generalization)

과적합 : 학습 데이터에 너무 치중하여, 새로운 데이터에 대해 예측력이 떨어지는 현상

해결 방법: 정규화, 교차 검증, 데이터 증강 등

편향-분산 트레이드오프(Bias-Variance Tradeoff)

편향(Bias): 모델이 단순해서 데이터의 복잡한 패턴을 충분히 반영하지 못하는 문제

분산(Variance): 모델이 너무 복잡해, 작은 데이터 변화에도 크게 흔들리는 문제

목표: 두 요소 사이의 균형을 찾아, 최적의 예측 성능을 달성

---

3. 게임 이론 기반 접근

3-1. 게임 이론의 기본 개념

정의:
여러 참가자(플레이어)가 서로의 전략을 고려하면서 의사결정을 내리는 상황을 분석하는 수학적 틀

<기본 용어>
플레이어(Player): 의사결정을 내리는 주체(예: 기업, 개인)

전략(Strategy): 각 플레이어가 선택할 수 있는 행동 방침

• 전략은 순수 전략(확정된 선택)과 혼합 전략(확률적으로 여러 선택 중에서 결정)이 있습니다.

보수(Payoff): 각 전략 조합에 따른 결과(이익 또는 손실)

균형(Equilibrium): 모든 플레이어가 자신의 전략을 바꾸지 않는 상태

정보(information) : 플레이어들이 게임 내에서 갖고 있는 정보의 양(완전 정보 vs 불완전 정보)에 따라 게임의 분석 방식이 달라짐
게임의 형태:

<게임의 형태>

정적 게임(Static Game) : 모든 플레이어가 동시에 또는 순서 없이 전략을 선택하는 게임.

동적 게임(Dynamic Game) : 플레이어들이 순차적으로 전략을 선택하며, 이전 플레이어의 선택이 이후 선택에 영향을 미칩니다.

완전 정보 게임(Perfect Information Game) : 모든 플레이어가 이전에 이루어진 행동이나 게임의 구조를 완전히 알고 있는 게임.

불완전 정보 게임(Imperfect Information Game) : 일부 정보가 숨겨져 있거나 불완전한 경우.

<게임의 표현 방식>

정규형 게임(Normal Form Game)

• 행렬 형태로 플레이어들의 전략과 그에 따른 보수를 나타냄 -> 각 플레이어의 전략 조합과 결과가 한눈에 들어오도록 표현

확장형 게임(Extensive Form Game)

• 게임 트리를 사용하여 시간 순서에 따라 플레이어들이 내리는 결정과 그 결과를 나타냄
• 순차적 의사결정을 분석할 때 유용

3-2. 내쉬 균형 (Nash Equilibrium)

• 개념:
  모든 플레이어가 상대방의 전략을 고려한 후, 더 이상 자신의 전략을 변경할 유인이 없는 상태

• 특징:
  내쉬 균형은 게임이 여러 개 존재할 수 있으며, 때로는 순수 전략 균형이 없고 혼합 전략 균형으로 나타나기도 합니다.

• 비유:
  두 사람이 동시에 무엇을 먹을지 결정할 때, 둘 다 서로의 선택을 알고 최적의 선택을 하게 되는 상황. 이 때 어느 한 쪽도 선택을 바꿀 이유가 없는 상태가 내쉬 균형입니다.

• 응용:
  실제 입찰에서는 경쟁 업체들이 서로의 전략을 예상하면서 최적의 투찰 금액을 결정하게 됩니다.

3-3. 추가 개념

순수 전략: 플레이어가 특정 행동을 확실하게 선택하는 전략

혼합 전략:

• 정의:
  플레이어가 여러 순수 전략을 일정 확률로 선택하는 전략입니다.

예:
매칭 페니(Matching Pennies) 게임에서 두 플레이어는 동전 앞면 또는 뒷면을 선택하는데, 한 플레이어는 상대방의 선택을 예측할 수 없도록 확률적으로 전략을 섞어 사용합니다.

• 균형:
  혼합 전략 균형은 각 플레이어가 상대의 전략에 대해 자신의 기대 보수를 최대화할 수 있는 확률 분포를 찾는 것입니다.

• 제한된 합 게임(Non-zero-sum game):
  모든 플레이어의 이익이 반드시 한쪽의 손실로 귀결되지 않는 게임 상황

---

4. 베이지안 추론

4-1. 기본 개념

베이즈 정리(Bayes' Theorem):

• 새로운 데이터가 주어졌을 때,기존 확률(사전 확률)을 업데이트하여 사건이 발생할 확률(사후 확률)을 계산하는 방법

전체 확률 공식 활용
베이즈 정리를 계산하려면 전체 확률

P(B)=P(B∣A)P(A)+P(B∣¬A)P(¬A)
이는 "검사 양성"이라는 사건이 "병 있음" 또는 "병 없음" 두 경우 모두에서 발생할 가능성을 더한 값입니다.

• 조건부 독립성
  베이즈 정리는 변수 간 독립성이 없더라도 조건부 독립성을 가정하여 계산
  EX) 환자의 나이가 병에 영향을 줄 수 있지만 검사 결과와 독립일 수 있음

4-2. 베이지안 네트워크(Bayesian Network)

• 정의:
  변수들 간의 확률적 관계를 그래프로 표현하는 방법입니다.

노드(Node) : 변수

엣지(Edge) : 변수 간의 인과 관계(조건부 의존성)

• 역할:
  복잡한 확률 모델에서 변수들 간의 관계를 시각화하고, 확률 업데이트를 쉽게 수행

4-3. 변분 추론(Variational Inference)

• 개념:
  복잡한 베이지안 모델의 사후 확률을 근사하는 방법입니다.

• 원리:
  복잡한 분포 대신 계산하기 쉬운 분포(예: 가우시안)를 사용해 근사하고, 이 근사 분포가 실제 사후 분포에 가까워지도록 최적화합니다.

• 비유:
  어려운 퍼즐 문제를 직접 풀기보다는, 비슷한 형태의 더 간단한 퍼즐로 대체하여 풀어내는 것과 비슷합니다.

4-4. 베이지안 추론의 장점과 단점

장점

• 불확실성 관리: 데이터가 부족하거나 불확실한 상황에서 사전 정보를 효과적으로 활용할 수 있습니다.

• 연속적 업데이트: 새로운 데이터가 들어올 때마다 기존의 믿음을 업데이트하여 점진적으로 개선 가능

단점

• 계산 비용: 특히 복잡한 모델에서는 계산량이 많아질 수 있습니다.

• 사전 확률 설정: 올바른 사전 정보를 선택하는 것이 어렵고, 결과에 큰 영향을 미칠 수 있습니다.

---

종합 정리

통계적 회귀 모델

• 기본 이론: 선형 회귀, 로지스틱 회귀

• 핵심 개념: 독립/종속 변수, 최소제곱법, 시그모이드 함수

• 특징: 단순하고 빠르지만, 복잡한 비선형 관계는 포착하기 어려움

머신러닝 모델

• 기본 이론: 지도 학습, 비지도 학습, 강화 학습

• 핵심 알고리즘: 랜덤 포레스트, XGBoost, 신경망

• 추가 개념: 과적합, 편향-분산 트레이드오프

• 특징: 복잡한 데이터 패턴을 학습할 수 있으나, 많은 데이터와 계산 자원이 필요

게임 이론 기반 접근

• 기본 이론: 플레이어, 전략, 보수, 균형

• 핵심 개념: 내쉬 균형, 순수 전략, 혼합 전략

• 특징: 경쟁 상황에서의 상호작용을 모델링하지만, 계산이 복잡하고 현실의 변수들을 모두 반영하기 어려울 수 있음

베이지안 추론

• 기본 이론: 베이즈 정리

• 핵심 개념: 사전 확률, 우도, 사후 확률, 베이지안 네트워크, 변분 추론

• 특징: 불확실성을 효과적으로 다루며, 새로운 데이터로 지속적으로 업데이트 가능하지만, 계산량이 많고 초기 설정이 중요

---

<투찰 시뮬레이션>
players

• pre_data의 모듈을 통해 사전에 생성된 플레이어 객체가 사용됨
• 각각의 플레이어는 pq_score를 가지고 있음 -> 투찰결과에 영향을 줌

Strategy

• player가 선택하는 투찰 가격 = 전략
• generate_random_bid 함수 => 특정 구간 내에서 랜덤으로 투찰가격을 결정,
• 목표 가격평점 계산하는 함수 사용

---

로지스틱 회귀 참고자료 - https://aws.amazon.com/ko/what-is/logistic-regression/