1. 베이지안 통계 및 실습

• 통계학의 주요 접근법
  빈도주의 : 데이터를 통해 사건의 빈도를 계산하고, 확률을 반복 실험의 결과로 이해
  베이지안 접근법 : 기존의 믿음(사전 정보)을 수치화하여(사전분포) 데이터를 관찰한 후 이 믿음을 업데이트 하는 방식(사후분포)을 사용

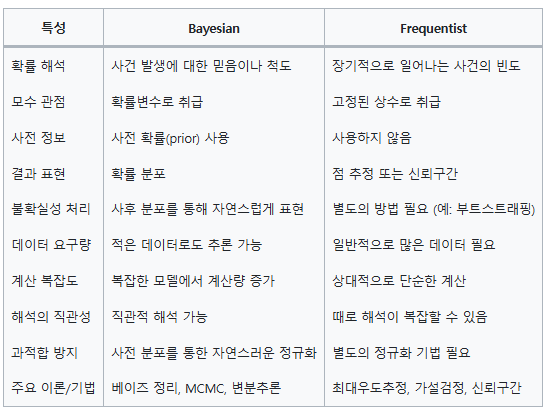
• 두 접근법의 주요 차이점
  확률 해석:

Frequentist: 확률을 장기적인 사건의 빈도로 해석합니다.
Bayesian: 확률을 사건 발생에 대한 믿음 또는 주관적 척도로 해석합니다.
모수(Parameter) 취급:

Frequentist: 모수를 미지의 고정된 상수로 간주합니다.
Bayesian: 모수를 확률적으로 변하는 확률변수로 취급합니다.
사전 정보의 활용:

Frequentist: 주로 현재 데이터에만 의존합니다.
Bayesian: 사전 정보를 명시적으로 모델에 통합합니다.
불확실성 처리:

Frequentist: 주로 점 추정과 신뢰구간을 사용합니다.
Bayesian: 모수의 전체 확률 분포를 통해 불확실성을 표현합니다.
계산 복잡성:

Frequentist: 일반적으로 계산이 상대적으로 단순합니다.
Bayesian: 복잡한 사후 분포 계산이 필요할 수 있어 계산량이 많을 수 있습니다.

<개념>
사전분포(prior): 데이터 관측 전,우리에게 있는 정보나 믿음을 수학적으로 표현한 것입니다. 예를 들어, 동전의 앞면이 나올 확률에 대해 ‘동전은 공평하다’라는 믿음을 반영할 때 사용됩니다.

우도(likelihood): 데이터를 통해 모델이 얼마나 잘 설명되는지를 나타내는 함수입니다. 관찰된 데이터가 주어졌을 때, 모델이 이 데이터를 만들어낼 확률로 생각할 수 있습니다.

사후분포(posterior): 관찰된 데이터를 바탕으로 사전분포를 업데이트한 결과입니다. 이제 우리가 원하는 모수(parameter)의 분포를 갖게 됩니다.

확률 기초 및 베이지안 기초 수학

• 확률 분포 및 조건부 확률
  확률 분포는 변수의 가능한 값들과 각 값이 발생할 확률을 의미
• 조건부 확률 : 어떤 사건이 일어났을 때 다른 사건이 일어날 확률 -> 베이즈 정리의 근본 원리

베이즈 정리

사후분포∝우도×사전분포

사전분포 설계와 선택

비정보적 vs. 정보적 사전분포:

비정보적 사전분포(noninformative prior): 이전에 특별한 정보가 없을 때 사용하며, 가능한 모든 값에 대해 거의 평평한(일정한) 확률을 부여합니다.

정보적 사전분포(informative prior): 과거 연구나 경험 등으로부터 얻은 구체적 정보를 반영합니다.

공액 사전분포(conjugate prior):
특정한 우도 함수와 결합하면 사후분포가 같은 분포 형태를 유지하는 사전분포입니다. 예를 들어, 베르누이 모형에서는 베타분포가 공액 사전분포로 활용됩니다.

사후분포 유도와 해석

사후분포

• 관측 데이터가 주어졌을 때 모수의 분포
• 사후분포는 데이터가 모수에 대해 어떤 정보를 제공하는지, 모수에 대한 불확실성이 얼마나 남아있는지 직관적으로 나타냄

베이지안 추정 및 결정 이론

점 추정 vs 구간추정
점 추정

• 사후 분포에서 하나의 '요약'값을 선택하는 방법
  => 사후분포로 부터 단 하나의 값을 뽑아내는 것

• 사후분포에서 평균, 중앙값 또는 최빈값 등 한 가지 대표값을 뽑아내는 방법
  -> 이 대표값은 어떤 방식으로 "최적"이라고 평가될 수 있는 추정치

• 사후 평균: 사후분포의 평균 값

• 사후 중앙값: 50%의 누적 확률을 가지는 값

• 사후 최빈값 (MAP): 가장 가능성이 높은 값

구간추정

• 사후 분포 전체의 형태를 고려하여 모수가 포함될 확률이 높은 범위를 제시
• 구간 추정은 점 추정치만으로 포착할 수 없는 추정치의 불확실성을 정량적으로 표현한 것

왜 불확실성 반영이 중요한지 ?

• 전체 사후분포 : 하나의값 X, 모수가 취할 수 있는 여러 가능성을 확률적으로 보여주는 것 (점 추정은 물론 구간 추정까지 제공 가능)

손실함수와 베이지안 의사결정 이론

손실함수

• 추정 혹은 의사결정 과정에서 발생하는 "비용" 또는 "손실"을 수치화하는 함수
  

• 손실함수가 주어지면, 베이지안 분석가는 사후 분포를 이용해 각 추정 방법의 기대 손실을 계산하고, 이를 최소화하는 추정량을 선택합니다. 예를 들어, 특정 손실함수 하에서 점 추정량을 선택하는 과정은 "베이지안 추정"이라고 하며, 이는 실제로 손실 최소화를 기반으로 합니다.

베이지안 추론에서 손실함수의 구체적인 역할

• 최적 추정치 결정 : 손실함수를 최소화하는 추정치를 선택

  • 제곱 오차 손실을 사용할 때는, 사후분포의 평균이 기대 손실을 최소화합니다.

  • 절대 오차 손실을 사용할 때는, 사후분포의 중앙값이 최적의 추정치가 됩니다.

  • 0-1 손실 같은 경우에는 사후분포의 최빈값(모드)이 선택될 수 있습니다.

손실함수는 실제 의사결정 상황에서 어느 정도의 오차나 위험을 감수할 수 있는지(또는 감수해서는 안되는지)를 정해주므로, 추정 과정과 밀접하게 연관

예측 분포와 모델 평가 기법

예측분포

• 관측된 데이터를 바탕으로 미래의 또는 미관측 데이터x에 대한 분포를 나타냄
  => 우리가 얻은 사후분포를 활용하여, 아직 관찰하지 않은 새로운 데이터가 어떻게 나올지를 예측
  

• Bayes Factor:
  두 모델이 주어졌을 때, 각각의 데이터를 설명하는 정도를 비교하는 지표입니다. 수치가 높을수록 해당 모델이 데이터를 더 잘 설명한다고 판단합니다.

• DIC (Deviance Information Criterion):
  모델의 적합도와 복잡도를 같이 고려하는 지표입니다. 값이 낮으면 더 좋은 모델로 평가합니다.

수치적 통합 및 몬테카를로 기법

수치적 통합

• 수학적으로 적분이 어려울 때, 컴퓨터를 사용해 근사적으로 계산하는 방법입니다.
  예를 들어, 사후분포가 매우 복잡해서 적분이 어려운 경우 이를 근사하는 식

몬테카를로 기법

• 많은 무작위 샘플을 생성해서, 그 샘플들을 이용해 평균, 분산 같은 값을 추정하는 방법
• "반복적인 무작위적 샘플링"
  

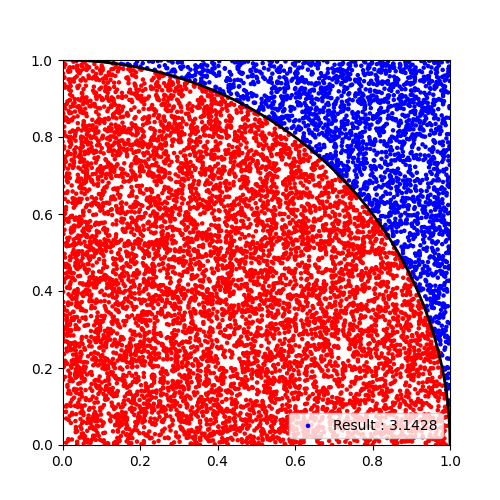
MCMC (Markov Chain Monte Carlo)

=> Markov Chain + Monte Carlo
Monte Carlo-> 반복적인 무작위적 샘플링(시뮬레이션)
Markov Chain -> 어떤 상태에서 다른 상태로 넘어갈 때, 바로 전 단계의 상태에만 영향을 받는 확률 과정

• 기본 개념:
  MCMC는 ‘마르코프 체인’이라는 연속된 상태를 만들어가며, 이 체인이 장시간 후에 목표하는 사후분포를 잘 반영하도록 합니다.

• 복잡한 분포:
  MCMC는 복잡한 사후 분포로부터 샘플을 생성하는 방법, 여기서 생성된 샘플은 사후 분포의 특성을 잘 반영하며, 이를 통해 평균, 분산, 신뢰구간 등 다양한 통계량을 근사할 수 있습니다.

• 기본 개념:
  MCMC는 ‘마르코프 체인’이라는 연속된 상태를 만들어가며, 이 체인이 장시간 후에 목표하는 사후분포를 잘 반영하도록 합니다.
  참고 자료 : https://angeloyeo.github.io/2020/09/17/MCMC.html

MCMC가 베이지안 이론에 사용되는 이유?

• 사후분포는 이론적으로 정확한 값:
  베이지안 정리에 따라 사전분포와 우도를 사용해 "정확한" 사후분포를 정의할 수 있습니다.

• 실제 문제에서는 닫힌 해가 어려움:
  실제 복잡한 모델에서는 이 사후분포가 해석적으로 표현하기 어려운 "더럽게 복잡한" 형태가 되고, 이를 직접 계산하기 어렵습니다.

• MCMC의 역할:
  MCMC는 그러한 복잡한 사후분포에서 많은 시뮬레이션을 통해 샘플을 생성함으로써, 이론적으로 정의된 사후분포를 근사하게 하고, 이 근사된 분포로부터 평균, 중앙값 등의 점 추정량을 도출하는 데 도움을 줍니다.

MCMC에서 Markov Chain의 역할:

• Markov Chain은 "현재 상태에 기반한 다음 상태 결정"이라는 규칙을 통해 샘플을 생성합니다. 이 때, 전체 체인(연속된 샘플의 집합)이 충분히 길어지면, 이 샘플들의 분포가 우리가 계산하고자 했던 사후분포와 거의 같아지게 됩니다.
• 이 규칙을 반복하다 보면, 전체 체인(샘플들)이 목표한 사후분포와 동일한 분포를 갖게 됩니다.

<MCMC의 주요 알고리즘 예시>

Metropolis–Hastings
과정 요약:

현재 상태에서 새로운 후보 값을 제안합니다.

후보 값을 목표 분포(예: 사후분포)와 비교해 수용 확률(acceptance probability)을 계산하고, 이 확률에 따라 후보를 채택하거나 현재 상태를 유지

=> 제안-수용/거부 방식을 통해 샘플을 생성하는 구체적인 알고리즘

쉽게 말하면:
“현재 위치에서 조금씩 이동하면서, 이동할 때마다 ‘이쪽이 더 좋은가?’를 판단하는 방식”이라고 이해할 수 있습니다.

깁스 샘플링 (Gibbs Sampling)
아이디어:
다변량 분포(여러 변수가 있는 경우)에 대해, 각 변수의 조건부 분포를 차례로 샘플링하는 방식입니다.

예시:
두 변수가 있을 때, 먼저 X를 고정하고 Y의 값을 뽑고, 다시 Y를 고정하고 X를 뽑는 것을 반복함으로써 전체 분포를 근사합니다.

고급 MCMC 기법과 확장

Hamiltonian Monte Carlo (HMC)
핵심 개념:
물리학의 운동 법칙을 모방하여, 고차원 공간(변수가 많은 경우)에서도 효율적으로 샘플을 생성합니다.

장점:
단순 랜덤 워크보다 빠르고, 더 잘 섞여(혼합) 전체 분포를 빠르게 탐색할 수 있습니다.

No-U-Turn Sampler (NUTS)
정의:
HMC의 단점을 보완해, 샘플링 경로가 과도하게 길어지거나 되돌아가지 않도록 자동으로 제어하는 알고리즘입니다.

활용:
Stan, PyMC3와 같은 최신 베이지안 라이브러리에서 사용

---

새롭게 알게된 사실
물리적 차원 VS 추상적 차원

• 물리적 차원 : 우리가 경험하는 세계는 3차원 공간(길이, 너비, 높이)으로 구성

• 물체의 위치(X, Y, Z)

• 통계적/수학적 차원 :
  통계나 머신러닝, 베이지안 모델에서는 각 변수나 모수가 하나의 차원으로 취급

• EX. 10개의 서로 다른 변수(특징)를 가진 데이터를 다룬다면 -> 10차원 공간의 한 점으로 표현(물리적 공간이 아닌 데이터나 모수를 표현하는 추상적인 좌표축)

---

참고자료 :
베이지안 이론 - https://bioinformaticsandme.tistory.com/47
https://velog.io/@euisuk-chung/%EC%9A%A9%EC%96%B4%EC%A0%95%EB%A6%AC-%EB%B9%88%EB%8F%84%EC%A3%BC%EC%9D%98Frequentist-VS-%EB%B2%A0%EC%9D%B4%EC%A7%80%EC%95%88Baysian
https://bioinformaticsandme.tistory.com/42
공고- https://www.wanted.co.kr/wd/259136?client_id=KK03NuM8GrpMbYP7vrf8FxsI