1. 수리 통계 1 : 기초 통계 추론과 이론의 탄탄한 기초 마련
1-1. 표본분포
정의 :
- 모집단에서 동일한 크기의 표본을 무수히 많이 추출하여 계산한 통계량(예: 평균, 분산, 중앙값 등)의 분포
- 모집단에서 표본만을 뽑아 통계량을 계산하면 값들이 조금씩 달라짐 -> 표본에서 나온 통계량들이 나타내는 분포
EX) 예를 들어, 학교 전체 학생의 키를 알 수 없을 때, 30명의 학생을 여러 번 뽑아서 평균 키를 계산하면, 매번 조금 다른 평균이 나오는데, 이들이 모인 분포가 표본분포
1-2.확률 변수의 독립성 및 중심극한정리(Central Limit Theorem, CLT)
독립성
정의:
두 확률 변수 X와 Y가 서로 독립적이라는 것은, X의 결과가 Y의 결과에 어떠한 영향을 주지 않는다는 의미입니다.
수학적으로, 임의의 x와 y에 대해 P(X≤x,Y≤y)=P(X≤x)⋅P(Y≤y)
라는 성질을 만족합니다.
예시:
동전을 두 번 던졌을 때 첫 번째 던짐의 결과(앞면 혹은 뒷면)는 두 번째 던짐의 결과에 영향을 주지 않습니다.
중심극한정리(CLT):
정의:
표본의 크기 n이 충분히 크면, 개별 확률 분포가 어떠하든지 간에, 독립적인 표본들로 구성된 표본 평균의 분포는 근사적으로 정규분포에 가까워진다는 정리입니다.

- CLT는 실제 데이터를 분석할 때 복잡한 분포를 단순화하는 역할을 함
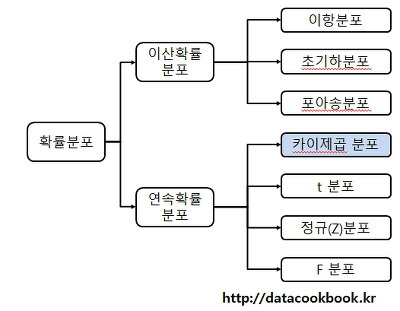
1-3. 다양한 확률분포
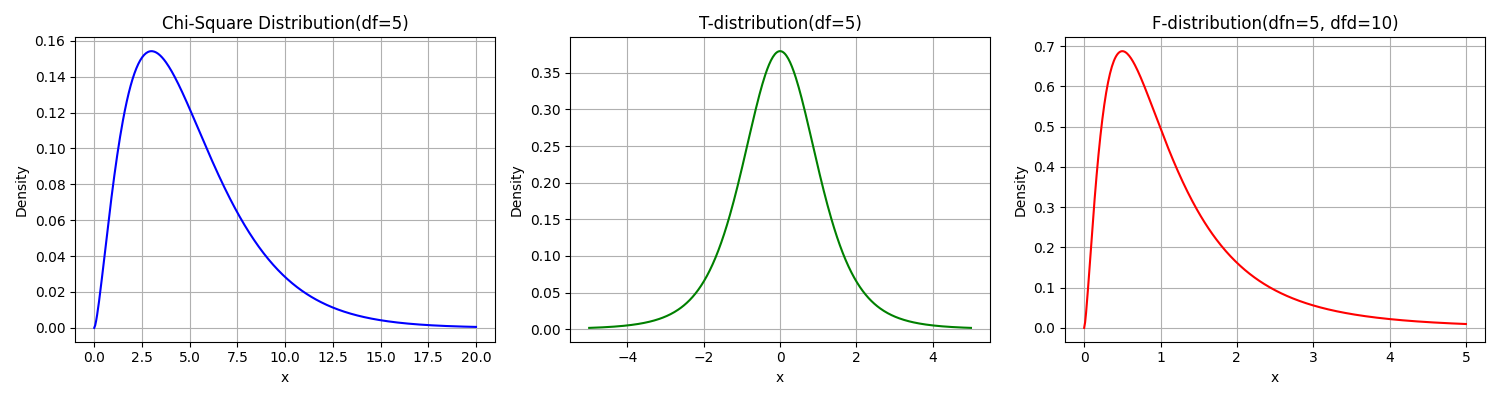
카이제곱 분포 : 표본 분산이나 분산의 추정을 할 때 활용, N개의 독립 정규 분포 변수의 제곱합이 따라짐
- 독립적인 표준 정규 분포 변수들의 제곱합으로 구성됩니다.
(예: Z₁, Z₂, …, Zₙ이 독립인 표준 정규 변수라면, χ² = Z₁² + Z₂² + … + Zₙ²)
t-분포 : 표본평균에서 모평균을 뺀 값을, 표본 표준편차로 나눴을 때 나타나는 분포
- 작은 표본의 경우 정규분포 대신 사용, 모평균 추정의 불확실성을 보완할 때 이용
F-분포 : 두 개의 독립적인 카이제곱 분포를 각각의 자유도로 나눈 값의 비율로 구성됩니다.
(즉, F = (χ²₁/df₁) / (χ²₂/df₂))
두 개의 표본 분산을 비교할 때 사용, 분산분석(ANOVA)에서 주요한 역할함

1-4. 확률변수의 함수와 Jacobian 기법
함수 변환의 개념
- 확률변수 x가 주어졌을 때, Y=g(x)와 같이 함수로 변환하면 y 또한 확률분포를 가지게 됨
-> 원래 분포를 fx(x)라고 할 때, 변환된 분포fy(y)를 구하는 것이 목표
Jacobian기법
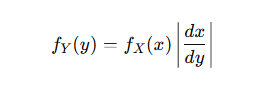
1-5. 기초 추정 이론
모멘트 추청
- 표본의 모멘트를 이용하여 모수를 추정하는 방법
최대가능도 추청(Maximum Likelihood Estimation, MLE)
- 주어진 데이터가 관측될 확률(우도함수)을 최대화 하는 모수를 찾는 방법


2. 수리 통계 2
2-1. 가설 검정 (Hypothesis Testing)
목적:
“무엇이 사실인가?”를 결정하기 위해, 데이터에 기초하여 어떤 가정(가설)을 채택할지 판단합니다.
예를 들어, “새로운 치료법이 기존 치료법보다 효과가 있다”라는 주장에 대해 데이터를 통해 검증할 때 사용합니다.
귀무가설과 대립가설
귀무가설 (Null Hypothesis,
보통 “차이가 없다”, “효과가 없다”와 같은 기본 가정을 말합니다.
예: 두 집단의 평균에 차이가 없다는 가정.
대립가설 (Alternative Hypothesis,
귀무가설과 반대되는 주장입니다.
예: 한 집단의 평균이 다른 집단의 평균보다 크다거나 작다는 주장을 의미합니다.
단측 vs. 양측 검정
단측 검정 (One-tailed test):
특정 방향으로의 차이만을 확인합니다.
예시: “신약이 기존 약보다 효과가 좋다”라고 할 때, 단지 신약의 효과가 더 크다는 증거만 찾고자 함.
양측 검정 (Two-tailed test):
차이가 존재하는지만 확인합니다.
예시: “신약과 기존 약의 효과가 다르다”는, 어느 한쪽으로 더 크다는 것뿐 아니라 양쪽 모두 차이를 검토함.
p-value (유의확률)
정의:
귀무가설이 참이라는 가정 하에서, 우리가 관측한 데이터(또는 더 극단적인 데이터)가 나타날 확률.
해석:
작은 p-value (일반적으로 0.05 이하)는 관측된 데이터가 귀무가설 하에서는 발생하기 어려워 귀무가설을 기각하게 만드는 근거가 됩니다.
예시:
만약 p-value가 0.02라면, “우연히 이런 결과가 나올 확률이 2%밖에 안 된다”는 뜻이므로 귀무가설을 기각하고, 대립가설을 채택할 가능성이 높습니다.
일반적인 기준
- p-value < 0.05: 통계적으로 유의미하다 → 귀무가설 기각
- p-value ≥ 0.05: 통계적으로 유의미하지 않다 → 귀무가설 채택
<오류의 유형>
제1종 오류 (Type I Error):
실제로 차이가 없는데(귀무가설이 참임에도 불구하고) 차이가 있다고 잘못 판단하는 오류.
예: 치료 효과가 없는데도 효과가 있다고 결론 내림.
제2종 오류 (Type II Error):
실제로 차이가 있는데(대립가설이 참임에도 불구하고) 차이가 없다고 잘못 판단하는 오류.
예: 효과가 있는 치료법을 효과 없다고 판단.
2-2. 추정량의 점근적 성질(Asymptotic Properties)
대표본 이론
- 표본이 모집단의 특성을 잘 반영하는가를 다루는 개념
- 표본의 크기가 충분히 크면, 표본의 통계량이 모집단의 특성을 잘 대표하게 됨
- 중심극한정리에 따라, 표본 평균이나 표본 비율은 표본 크기가 커질수록 정규분포에 근사함
점근 분포
정의:
"점근"이라는 단어는 표본 크기가 매우 클 때(수렴하는 경우)를 의미합니다.
대규모 표본을 모았을 때, 추정치(예: 표본 평균)의 분포가 특정한 모양(예, 정규분포)에 가까워진다는 것이 대표본 이론입니다.
예시:
만약 동전을 던져서 앞면이 나오는 비율을 구할 때, 표본이 1000회 이상이면 표본 비율의 분포는 정규분포에 근사하게 됩니다.
일관성 (Consistency)
정의:
추정량이 표본 크기가 커질수록 실제 모수에 점점 가까워지는 성질입니다.
즉, n→∞일 때 θ에 “수렴”합니다.
예시:
동전 던지기의 경우, 표본 크기가 작을 때는 앞면 비율이 다소 편차가 있으나, 표본이 매우 많아지면 실제 앞면 발생 확률(예: 0.5)에 가까워집니다.
중앙극한정리의 심화
심화 내용:
단순히 평균이 정규분포에 근사한다는 것뿐 아니라, 다른 통계량(예: 분산, 비율)도 충분한 표본 크기에서 정규분포로 근사될 수 있음을 연구합니다.
활용:
복잡한 통계 검정을 할 때 이론적 기반을 제공하며, 데이터를 통해 얻은 추정량의 분포 형태를 예측하는 데 사용됩니다.
2-3. 충분통계량
충분통계량
- 주어진 모수에 관한 모든 정보를 데이터에서 "압축"해 담고 있는 통계량
- 원래 데이터를 모두 봐야할 필요 없이 모수에 관한 모든 중요한 정보를 얻을 수 있음
팩토르라이제이션 정리
- 어떤 통계량이 충분통계량인지 확인하는 방법을 제공
- 데이터의 확률 밀도 함수가 “모수 정보가 포함된 부분”과 “그 외의 부분”으로 나눠질 수 있으면, 그 나눠진 부분에 해당하는 함수값이 충분통계량임을 보이는 방법
2-4. 크래머 - 라오 부등식(Cramer-Rao Inequality)
- 불편 추정량이 가질 수 있는 분산의 최소 한계를 제시
=> 어떤 추정량도 이 한계보다 분산(오차)이 작을 수 없다는 기준을 알려주는 것
효율적 추정량
- 크래머-라오 부등식에서 제시한 최소 분산 한계(최저 오차)를 실제로 달성하는 추정량
피셔정보
- 데이터가 모수에 대해 얼마나 많은 정보를 주는지를 나타냄 -> 이론상 달성할 수 있는 최소 오차(정확한 추정)를 낼 수 있음
3. 회귀 분석 및 실습 : 모델링과 데이터 분석의 실제 주요 학습 내용 및 개념
3-1. 단순 선형 회귀 분석
- 두 변수 간의 관계를 직선 형태로 모델링하여, 독립 변수가 종속 변수에 미치는 영향을 파악하고 예측
최소 제곱법
- 주어진 데이터를 기준으로 "예측 직선"을 찾는데, 이 직선은 각 데이터 포인트와 직선 간의 수직 거리를 제곱한 값의 합(잔차 제곱합)이 최소가 되도록 결정
잔차 분석
- 각 데이터 포인트에 대해 실제 값과 모델이 예측한 값의 차이
3-2. 다중 선형 회귀 분석
- 여러 독립 변수들이 한 종속 변수에 미치는 영향을 동시에 분석
다중 공선성 문제 (Multicollinearity)
정의:
독립 변수들 사이에 높은 상관관계가 존재하면, 각 변수의 효과를 명확하게 분리하기 어려워집니다.
문제점:
계수 추정치의 분산이 커져서 해석이 어려워집니다.
모델의 안정성이 떨어지고, 변수의 중요성을 정확히 평가할 수 없게 됩니다.
해결 방안:
상관관계 높은 변수 중 하나를 제거하거나 변수를 결합하는 방법
Ridge, LASSO 회귀 등의 정규화 기법을 적용하여 변수 선택 및 계수 조정을 수행합니다.
모형 비교 기준 (AIC, BIC)
AIC (Akaike Information Criterion):
모델의 적합도와 복잡도(변수 수)의 균형을 고려하는 지표로, 값이 작을수록 좋은 모델로 평가합니다.
BIC (Bayesian Information Criterion):
AIC와 유사하지만, 데이터 수에 따라 패널티가 더 강하게 부여되어, 복잡한 모델보다 단순한 모델을 선호하는 경향이 있습니다.
헷갈렸던 부분
-
대표본 이론 vs 중심극한정리의 관계와 차이
대표본 이론(표본이 모집단을 잘 반영하는지)
-> 핵심 "모집단 전체의 성격을 잘 나타내는 샘플을 뽑는 것이 중요" -
중심극한정리(CLT)
-> 핵심 "샘플 평균의 특성"
<둘의 관계>
대표본 이론:
"우리의 샘플이 정말 모집단 전체를 제대로 대표하고 있는가?"에 집중합니다. (즉, 샘플을 어떻게 뽑느냐가 중요합니다.)
중심극한정리:
"샘플 평균을 여러 번 뽑으면 그 분포가 어떻게 되나?"에 집중합니다. (즉, 샘플의 평균이 정규분포에 가까워진다는 점)
자코비안 참고자료 - https://angeloyeo.github.io/2020/07/24/Jacobian.html
