[신경망기초]forward pass, backward pass에 대한 수학적 이해

민서·2024년 3월 24일
ML/DL신경망기초
0

신경망기본

목록 보기
1/4

들어가기 앞서

  • 이 게시글은 Deep learning from scarch, seth Weidman을 공부하고 작성한 게시물입니다.
  • 공부 기록과 추후 복기를 위해 작성하였기 때문에, 책 없이 게시물만 보고 공부하기에는 설명의 한계가 있습니다.

신경망

신경망이란?

신경망이란 무엇인가? 에 대한 물음의 답을 한다면 아래 4개의 문장으로 이루어 질 수 있다.

  • 신경망은 입력과 출력을 갖는 함수다.
  • 신경망은 다차원 배열이 흘러가는 계산 그래프다.
  • 신경망은 여러 개의 '층'으로 구성되며, 층은 다시 여러 개의 '뉴런'으로 구성된다.
  • 신경망은 어떤 함수라도 근사할 수 있는 능력(universal function approximator)이 있으며, 이론적으로 모든 지도 학습문제를 풀 수 있다.

각각의 4문장을 완전히 이해하려면 합성함수나 함성함수의 도함수 등등 여러 멘탈모델들의 완벽한 이해가 전제되어야 하고, 각 문장들이 서로 어떤 관계를 갖는지까지 모두 이해해야한다.

진행

신경망의 이론적 이해를 위해, 이번 글에서는기초적인 수학적인 모델을 정리할 것이다.
각각의 기초적인 멘탈모델의 기본적인 구성요소를 아래 세 가지 관점에서 설명한다.

  • 수식 : 수식 형태로 설명한다.
  • 코드 : 간단한 문법만을 사용해 설명한다.
  • 다이어그램 : 다이어그램을 통해 구조나 과정을 설명한다.

이해의 편의성을 위해 이 3가지의 순서는 바뀔 수 있다.

01. 함수

01.1 수식

아래에 두 예시함수가 있다.

f1(x)=x2f_1(x)=x^2
f2(x)=max(x,0)f_2(x)=max(x,0)

이 표기법은 우리가 임의로 f1f_1과 f2f_2라고 부르는 함수들이 숫자 xx를 입력으로 받아서 첫 번째 경우에는 &x^2&로, 두 번째 경우에는 max(x,0)max(x, 0)으로 변환한다는 것을 나타낸다.

01.2 다이어그램

수학적 표현

def square(x: ndarray) -> ndarray:
    '''
    인자로 받은 ndarray 배열의 각 요솟값을 제곱한다.
    '''
    return np.power(x, 2)

def leaky_relu(x: ndarray) -> ndarray:
    '''
    ndarry 배열의 각 요소에 'Leaky ReLU' 함수를 적용한다.
    '''
    return np.maximum(0.2 * x, x)

fig, ax = plt.subplots(1, 2, sharey=True, figsize=(12, 6))  # 2 Rows, 1 Col

input_range = np.arange(-2, 2, 0.01)
ax[0].plot(input_range, square(input_range))
ax[0].plot(input_range, square(input_range))
ax[0].set_title('Square function')
ax[0].set_xlabel('input')
ax[0].set_ylabel('output')

ax[1].plot(input_range, leaky_relu(input_range))
ax[1].plot(input_range, leaky_relu(input_range))
ax[1].set_title('ReLU function')
ax[1].set_xlabel('input')
ax[1].set_ylabel('output')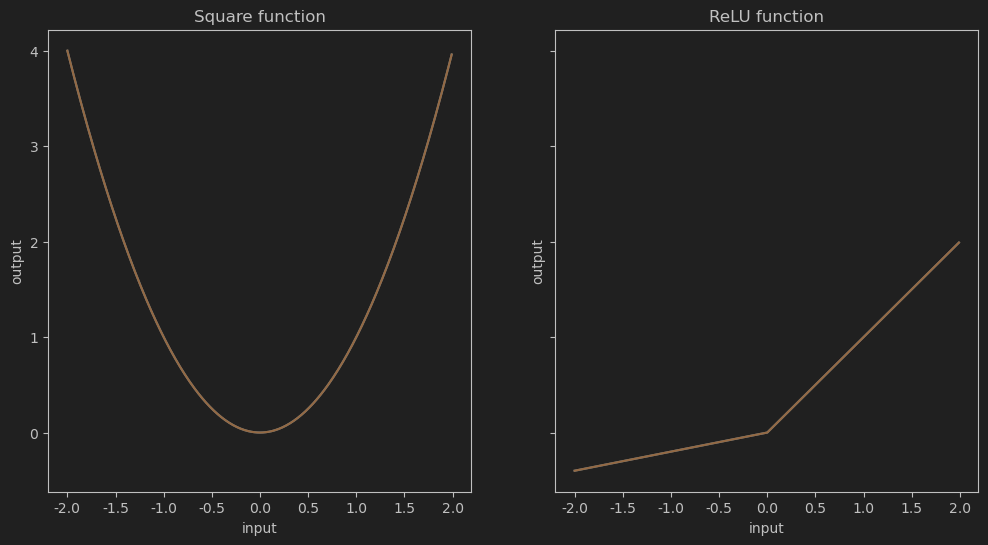


이는 x,y 축에 표현한 일반적인 함수의 도식적 표현이다. 르네 데카르트가 처음으로 제안했으며 수학의 많은 영역(특히 미적분학)에서 많이 사용한다.

딥러닝을 위한 표현


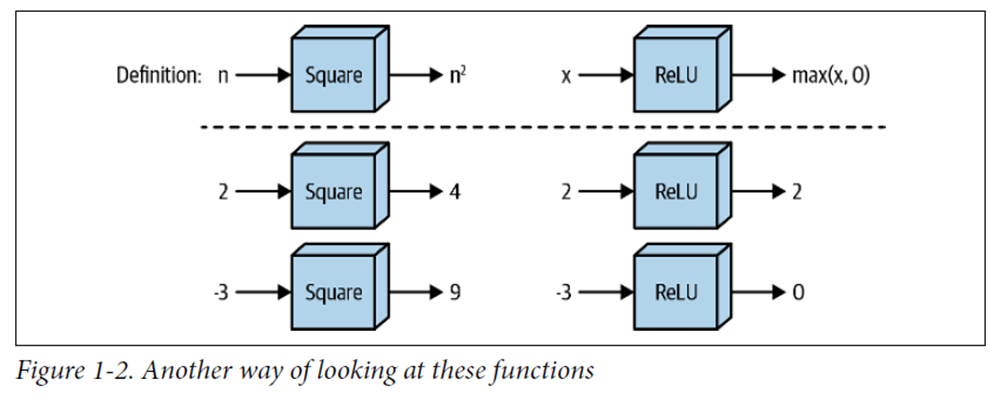
미적분학에는 그리 도움되지 않지만, 딥러닝 모델을 이해하는데 유용한 방법이다.
상자는 숫자로 입력값을 집어 넣으면 상자 안에 정의된 규칙에 따라 계산된 출력값이 튀어나온다.

01.3 코드

함수를 구현하기 이전 어떤 방법론으로 함수를 코드로 구현할지 생각해보자.

Numpy in python

넘파이는 고속 수치 연산분야에서 주로 사용되는 파이썬 라이브러리이다.
내부 대부분이 C로 구현되어있어 속도가 빠르다.
신경망에서 다루는 데이터는 모두 다차원 배열에 담기는데, 넘파이의 ndarray 클래스를 사용하면 직관적이고 효율적으로 다룰 수 있다.

elementwise calculation

또한, 파이썬의 기본 list와 달리 요소단위(elementwise) 덧셈 혹은 곱셈을 수행할 수 있다. 간단한 예시는 아래와 같다.

list1 = [1, 2, 3]
list2 = [4, 5, 6]
print(list1 + list2)  # Output: [1, 2, 3, 4, 5, 6]

scalar = 2
print(list1 * scalar)  # Output: [1, 2, 3, 1, 2, 3]

파이썬 리스트를 활용한 연산이다. elementwise 연산을 수행할 수 없다.

import numpy as np

array1 = np.array([1, 2, 3])
array2 = np.array([4, 5, 6])
print(array1 + array2)  # Output: array([5, 7, 9])

scalar = 2
print(array1 * scalar)  # Output: array([2, 4, 6])

numpy 라이브러리를 활용하면 이러한 연산이 가능하다.

axis calculation

직관적으로 특정 축을 선택해 해당 축의 방향으로 함수를 적용할 수도 있다.예를 들어 axis=0방향(2차원 배열의 열 방향) 합을 구하는 방법이 있다.

import numpy as np

# 2차원 배열 생성
arr = np.array([[1, 2], [3, 4]])

# axis=0 방향으로 합계 계산 (열 방향)
print('a.sum(axis=0):', a.sum(axis=0))  # Output: array([4, 6])

# axis=1 방향으로 합계 계산 (행 방향)
print('a.sum(axis=1):', a.sum(axis=1))  # Output: array([3, 7])

bias calculation(broadcastiong)

배열에 마지막 축의 방향으로 다른 1차원 배열을 합할 수 있다. 이는 배열의 곱셈에서 편향(bias)를 더할 때 활용된다. Ma∗b+M1∗bM_{a*b}+M_{1*b}연산을 확인해보면, 다음과 같이 2차원 배열에 열이 b개인 1차원 배열b를 각각 합하는 연산이 진행된다.

Ma∗b+M1∗b=[m11m12⋯m1bm21m22⋯m2b⋮⋮⋱⋮ma1ma2⋯mab]+[m1m2⋯mb]=[m11+m1m12+m2⋯m1b+mbm21+m1m22+m2⋯m2b+mb⋮⋮⋱⋮ma1+m1ma2+m2⋯mab+mb]M_{a*b} + M_{1*b} = \begin{bmatrix} m_{11} & m_{12} & \cdots & m_{1b} \\ m_{21} & m_{22} & \cdots & m_{2b} \\ \vdots & \vdots & \ddots & \vdots \\ m_{a1} & m_{a2} & \cdots & m_{ab} \end{bmatrix} + \begin{bmatrix} m_{1} & m_{2} & \cdots & m_{b} \end{bmatrix} = \begin{bmatrix} m_{11}+m_{1} & m_{12}+m_{2} & \cdots & m_{1b}+m_{b} \\ m_{21}+m_{1} & m_{22}+m_{2} & \cdots & m_{2b}+m_{b} \\ \vdots & \vdots & \ddots & \vdots \\ m_{a1}+m_{1} & m_{a2}+m_{2} & \cdots & m_{ab}+m_{b} \end{bmatrix}

import numpy as np

# 2차원 배열 생성
arr_2d = np.array([[1, 2, 3], [4, 5, 6]])

# 1차원 배열 생성 (bias)
bias = np.array([10, 20, 30])

# bias를 더함
result = arr_2d + bias

print(result)
"""
Output : 
[[11 22 33]
 [14 25 36]]
"""

타입을 확인하는 함수

https://velog.io/@kms39273/파이썬문법타입-어노테이션
이전에 정리해둔 내용과 같은 내용이다.
요약하자면, 함수 인자의 데이터타입과 리턴 데이터 타입을 아래와 같이 명시적으로 작성하여 실행해보지 않고 정보를 얻는다.

def leaky_relu(x: ndarray) -> ndarray:

입력되는 x가 narray Type이고, 출력 역시 narray Type타입임을 알 수 있다.

02. 도함수

도함수란 어떤 특정 지점에서 함수의 입력값 변화에 대한 함숫값(출력값)의 변화율이라는 사실에서 출발한다. 수식, 다이어그램, 코드 관점에서 도함수의 동작원리에 대한 멘탈 모델을 확립해보자.

02.1 수식

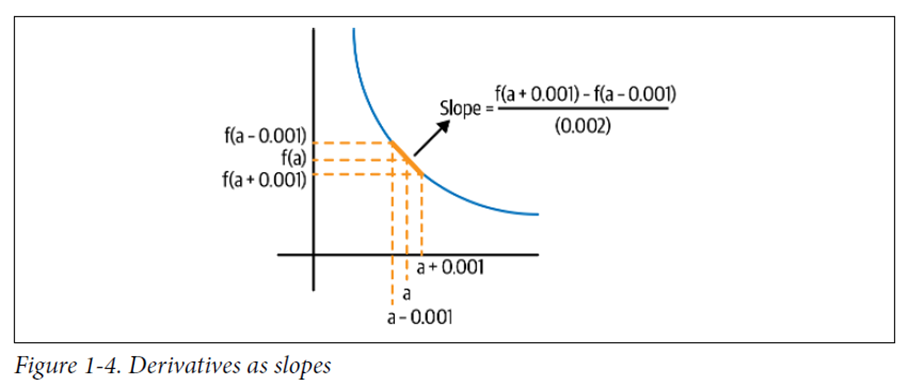
함수의 입력값에 대한 함숫값의 변화율을 정확히 계산하기 위해 극한을 이용한다.
dfdu(a)=lim⁡Δ→0f(a+Δ)−f(a−Δ)2Δ\frac{df}{du}(a) = \lim_{\Delta \to 0} \frac{f(a+\Delta) - f(a-\Delta)}{2\Delta}
Δ\Delta에 매우 작은 값, 예를 들어 0.001을 대입하는 방법으로 다음과 같이 표현된다.
dfdu(a)=f(a+0.001)−f(a−0.001)0.002\frac{df}{du}(a) = \frac{f(a+0.001) - f(a-0.001)}{0.002}

02.2 다이어그램


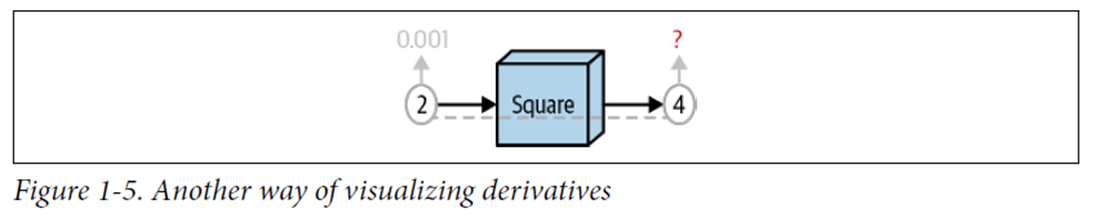
02.3 코드

from typing import Callable

def deriv(func: Callable[[ndarray], ndarray],
          input_: ndarray,
          diff: float = 0.001) -> ndarray:
    '''
    배열 input의 각 요소에 대해 함수 func의 도함숫값 계산
    '''
    return (func(input_ + diff) - func(input_ - diff)) / (2 * diff)

이는 도함수를 구하는 코드이다.

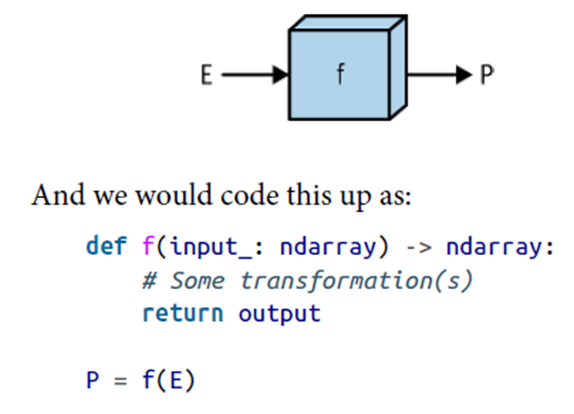
이 표현은 %f(E)=P%를 만족하는 함수 f가 있다는 것이다. 바꿔말하면 객체 E를 입력받아 객체 P를 내놓는 함수 f라는 뜻이다. 이것은 다시 P는 E에 의해 정의된다고 표현할 수 있다.

03. 합성함수

03.1 다이어그램


다이어그램을 통해 확인하는 것이 더 직관적이다.

03.2 수식

조금 덜 직관적인 수식을 이용해 표현해보자.
f1(f2(x))=yf_1(f_2(x))=y
f1f_1의 xx의 함숫값에 대한 f2f_2의 함숫값이다.

03.3 코드

from typing import List

# ndarray를 인자로 받고 ndarray를 반환하는 함수
Array_Function = Callable[[ndarray], ndarray]

# Chain은 함수의 리스트다.
Chain = List[Array_Function]

def chain_length_2(chain: Chain,
                   x: ndarray) -> ndarray:
    '''
    두 함수를 연쇄(chain)적으로 평가
    '''
    assert len(chain) == 2, \
    "인자 chain의 길이는 2여야 함"

    f1 = chain[0]
    f2 = chain[1]

    return f2(f1(x))

03.4 두번째 다이어그램


이는 함성함수를 나타내는 또다른 다이어그램이다.
다음은 합성함수의 도함수를 나타내는 방법을 알아보자.

04. 연쇄법칙(Chain Rule)

연쇄법칙을 이용해 합성함수의 도함수를 계산한다.
딥러닝 모델은 수학적으로 보면 합성함수이며, 딥러닝 모델 학습은 합성함수의 도함수가 활용된다.

04.1 수식

df2du(x)=df2du(f1(x))∗df1du(x)\frac{df_2}{du}(x)=\frac{df_2}{du}(f_1(x))*\frac{df_1}{du}(x)
*이때 u는 입력이 하나라고 가정할 때의 가변수이다.

04.2 다이어그램


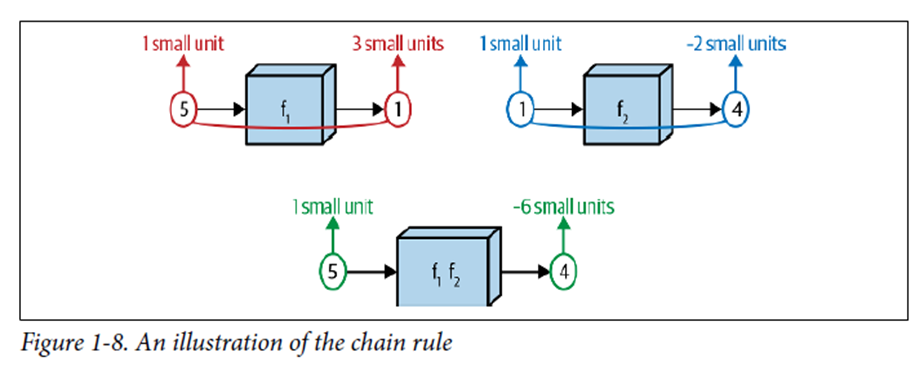
f_1(5)=1일때 도함숫값은 3이다.
f_2(1)=4일때 도함숫값은 -2이다.
따라서 합성함수의 도함숫값은 -6이다.
이는 위에 정리한 수식을 통해 알 수 있다.

04.3 코드

def square(x: ndarray) -> ndarray:
    '''
    인자로 받은 ndarray 배열의 각 요솟값을 제곱한다.
    '''
    return np.power(x, 2)

def sigmoid(x: ndarray) -> ndarray:
    '''
    입력으로 받은 ndarray의 각 요소에 대한 sigmoid 함숫값을 계산한다.
    '''
    return 1 / (1 + np.exp(-x))
    
# Chain은 함수의 리스트다.
Chain = List[Array_Function]

def chain_deriv_2(chain: Chain,
                  input_range: ndarray) -> ndarray:
    '''
    두 함수로 구성된 합성함수의 도함수를 계산하기 위해 연쇄법칙을 사용함
    (f2(f1(x))' = f2'(f1(x)) * f1'(x)
    '''

    assert len(chain) == 2, \
    "인자 chain의 길이는 2여야 함"

    assert input_range.ndim == 1, \
    "input_range는 1차원 ndarray여야 함"

    f1 = chain[0]
    f2 = chain[1]

    # df1/dx
    f1_of_x = f1(input_range)

    # df1/du
    df1dx = deriv(f1, input_range)

    # df2/du(f1(x))
    df2du = deriv(f2, f1(input_range))

    # 각 점끼리 값을 곱함
    return df1dx * df2du
    
def plot_chain(ax,
               chain: Chain, 
               input_range: ndarray) -> None:
    '''
    2개 이상의 ndarray -> ndarray 매핑으로 구성된 합성함수의
    그래프를 input_range 구간에 대해 작도함.
    
    ax: 작도에 사용할 matplotlib의 서브플롯
    '''
    
    assert input_range.ndim == 1, \
    "input_range는 1차원 ndarray여야 함"

    output_range = chain_length_2(chain, input_range)
    ax.plot(input_range, output_range)
    
def plot_chain_deriv(ax,
                     chain: Chain,
                     input_range: ndarray) -> ndarray:
    '''
    연쇄법칙을 이용해 합성함수의 도함수를 계산하고 그래프를 작도함.
    
    ax: 작도에 사용할 matplotlib의 서브플롯
    '''
    output_range = chain_deriv_2(chain, input_range)
    ax.plot(input_range, output_range)

fig, ax = plt.subplots(1, 2, sharey=True, figsize=(16, 8))  # 2 Rows, 1 Col

chain_1 = [square, sigmoid]
chain_2 = [sigmoid, square]

PLOT_RANGE = np.arange(-3, 3, 0.01)
plot_chain(ax[0], chain_1, PLOT_RANGE)
plot_chain_deriv(ax[0], chain_1, PLOT_RANGE)

ax[0].legend(["$f(x)$", "$\\frac{df}{dx}$"])
ax[0].set_title("$f(x) = sigmoid(square(x))$의 함수와 도함수")

plot_chain(ax[1], chain_2, PLOT_RANGE)
plot_chain_deriv(ax[1], chain_2, PLOT_RANGE)
ax[1].legend(["$f(x)$", "$\\frac{df}{dx}$"])
ax[1].set_title("$f(x) = square(sigmoid(x))$의 함수와 도함수");

# plt.savefig(IMG_FOLDER_PATH + "08_plot_chain_rule_1.png");
# plt.savefig(PDF_IMG_FOLDER_PATH + "08_plot_chain_rule_1.pdf");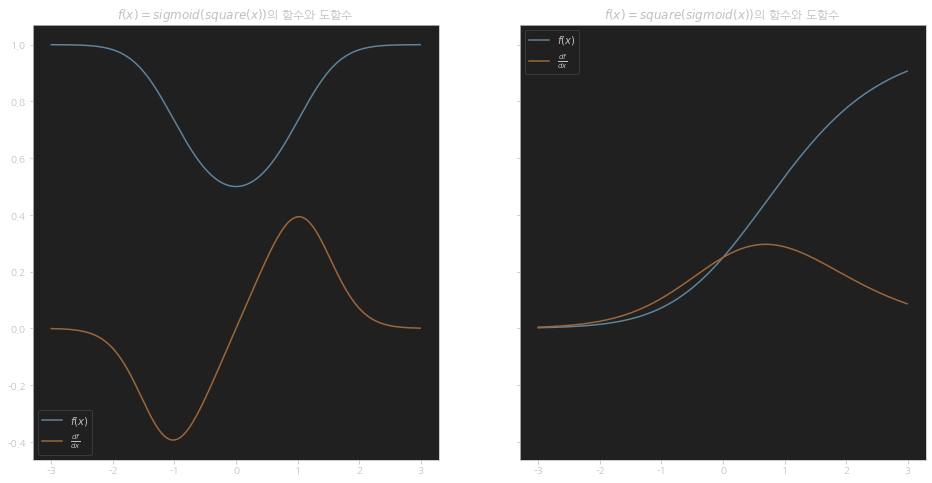

05. 복잡한 예제

05.1 수식

df3du(x)=df3du(f2(f1(x)))∗df2du(f1(x))∗df1du(x)\frac{df_3}{du}(x)=\frac{df_3}{du}(f_2(f_1(x)))*\frac{df_2}{du}(f_1(x))*\frac{df_1}{du}(x)

05.2 다이어그램

05.3 코드

def chain_length_3(chain: Chain,
                   x: ndarray) -> ndarray:
    '''
    3개의 함수를 연쇄적으로 평가함.
    '''
    assert len(chain) == 3, \
    "인자 chain의 길이는 3이여야 함"

    f1 = chain[0]
    f2 = chain[1]
    f3 = chain[2]

    return f3(f2(f1(x)))
def chain_deriv_3(chain: Chain,
                  input_range: ndarray) -> ndarray:
    '''
    세 함수로 구성된 함성함수의 도함수를 계산하기 위해 연쇄법칙을 사용함
    (f3(f2(f1)))' = f3'(f2(f1(x))) * f2'(f1(x)) * f1'(x)
    '''

    assert len(chain) == 3, \
    "This function requires 'Chain' objects to have length 3"

    f1 = chain[0]
    f2 = chain[1]
    f3 = chain[2]

    # f1(x)
    f1_of_x = f1(input_range)

    # f2(f1(x))
    f2_of_x = f2(f1_of_x)

    # df3du
    df3du = deriv(f3, f2_of_x)

    # df2du
    df2du = deriv(f2, f1_of_x)

    # df1dx
    df1dx = deriv(f1, input_range)

    # 각 점끼리 값을 곱함
    return df1dx * df2du * df3du
def square(x: ndarray) -> ndarray:
    '''
    인자로 받은 ndarray 배열의 각 요솟값을 제곱한다.
    '''
    return np.power(x, 2)

def leaky_relu(x: ndarray) -> ndarray:
    '''
    ndarry 배열의 각 요소에 'Leaky ReLU' 함수를 적용한다.
    '''
    return np.maximum(0.2 * x, x)

def sigmoid(x: ndarray) -> ndarray:
    '''
    입력으로 받은 ndarray의 각 요소에 대한 sigmoid 함숫값을 계산한다.
    '''
    return 1 / (1 + np.exp(-x))

3개의 함수와 3번 합성된 합성함수 미분 함수가 정의되었다.

def plot_chain(ax,
               chain: Chain, 
               input_range: ndarray,
               length: int=2) -> None:
               
    '''
    연쇄법칙을 이용해 합성함수의 도함수를 계산하고 그래프를 작도함.
    
    ax: 작도에 사용할 matplotlib의 서브플롯
    '''
    
    assert input_range.ndim == 1, \
    "input_range는 1차원 ndarray여야 함"
    if length == 2:
        output_range = chain_length_2(chain, input_range)
    elif length == 3:
        output_range = chain_length_3(chain, input_range)
    ax.plot(input_range, output_range)
def plot_chain_deriv(ax,
                     chain: Chain,
                     input_range: ndarray,
                     length: int=2) -> ndarray:
    '''
    연쇄법칙을 이용해 합성함수의 도함수를 계산하고 그래프를 작도함.
    
    ax: 작도에 사용할 matplotlib의 서브플롯
    '''

    if length == 2:
        output_range = chain_deriv_2(chain, input_range)
    elif length == 3:
        output_range = chain_deriv_3(chain, input_range)
    ax.plot(input_range, output_range)

그래프를 그리는 함수를 정의한 부분이다.

fig, ax = plt.subplots(1, 2, sharey=True, figsize=(16, 8))  # 2 Rows, 1 Col

chain_1 = [leaky_relu, square, sigmoid]
chain_2 = [leaky_relu, sigmoid, square]

PLOT_RANGE = np.arange(-3, 3, 0.01)
plot_chain(ax[0], chain_1, PLOT_RANGE, length=3)
plot_chain_deriv(ax[0], chain_1, PLOT_RANGE, length=3)

ax[0].legend(["$f(x)$", "$\\frac{df}{dx}$"])
ax[0].set_title("$f(x) = sigmoid(square(leakyRelu(x)))$의 함수와 도함수")

plot_chain(ax[1], chain_2, PLOT_RANGE, length=3)
plot_chain_deriv(ax[1], chain_2, PLOT_RANGE, length=3)
ax[1].legend(["$f(x)$", "$\\frac{df}{dx}$"])
ax[1].set_title("$f(x) = square(sigmoid(leakyRelu(x)))$의 함수와 도함수");

# plt.savefig(IMG_FOLDER_PATH + "09_plot_chain_rule_2.png");
# plt.savefig(PDF_IMG_FOLDER_PATH + "09_plot_chain_rule_2.pdf");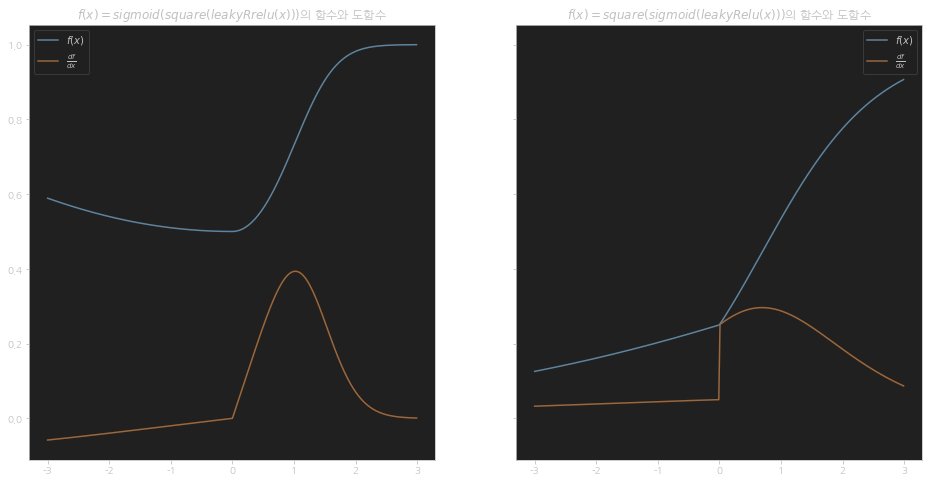


실행하며 연쇄법칙을 계산하는 단계가 두번 겹친다.
처음에 f1_of_x, f2_of_x를 계산하며 앞에서부터 합성함수를 거쳐가는 부분을 순방향 계산(forward pass)라고 부르며, 여기서 수한 함숫값을 통해 거슬러올라가며 도함수를 계산하는 부분(df3du, df2du, df1du)을 역방향 계산(backward pass)라고 부른다.

06. 입력이 두 개 이상인 함수의 합성함수

06.1 수식

다중 입력을 가진 함수
수학
만약 입력값이 xx와 yy라면, 이 함수를 두 단계로 생각해볼 수 있다.
첫 번째 단계에서, xx와 yy를 더하는 함수를 거치게 된다.
이 함수를 α\alpha라고 표시하고, 함수의 출력을 aa라고 표시해보자.

a=α(x,y)a = \alpha(x, y)

두 번째 단계에서는 aa를 어떤 함수 σ\sigma를 거치게 된다. (σ\sigma는 시그모이드 함수, 제곱 함수 또는 어떤 연속 함수도 될 수 있다.)
이 함수의 출력을 우리는 ss라고 표시하자.

s=σ(a)s=\sigma(a)

같은 방법으로 전체 합성함수ff를 다음과 같이 나타낼 수 있다.

f(x,y)=σ(x,y)f(x, y) = \sigma(x, y)

다이어그램으로 보자.

06.2 다이어그램

06.3 코드

def multiple_inputs_add(x: ndarray,
                        y: ndarray,
                        sigma: Array_Function) -> float:
    '''
    두 개의 입력을 받아 값을 더하는 함수의 순방향 계산
    '''
    assert x.shape == y.shape

    a = x + y
    return sigma(a)

07. 입력이 여러 개인 함수의 도함수

07.1 다이어그램


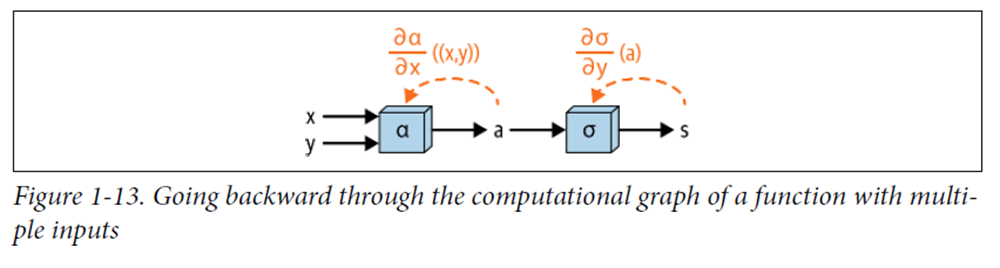
개념적으로 단일 입력을 가진 함수의 경우와 동일하게 진행된다.
계산 그래프를 "역으로" 거슬러 올라가며 각 구성 함수의 도함수를 계산하고, 그 결과를 곱하여 총 도함수를 얻는다.

07.2 수식

f(x,y)=c(a(x,y))f(x, y) = c(a(x, y))와 같은 함수가 있다면, 이것은 a(x,y)a(x, y)라는 함수와 c(a)c(a)라는 함수로 구성된 복합 함수이다.

연쇄 법칙에 따르면, 복합 함수의 도함수는 구성 함수의 도함수들의 곱으로 표현할 수 있다. 즉, f(x,y)f(x, y)의 xx에 대한 도함수는 c(a)c(a)의 aa에 대한 도함수와 a(x,y)a(x, y)의 xx에 대한 도함수의 곱으로 표현된다.

07.3 코드

def multiple_inputs_add_backward(x: ndarray,
y: ndarray,
sigma: Array_Function) -> float:
두 개의 입력 을 받는 함수의 두 입력에 대한 각각의 도함수 계산
# 정방향 계산 수행
a = x + y
# 도함수 계산
dsda = deriv(sigma, a)
dadx, dady = 1, 1
return dsda * dadx, dsda * dady

09. 기존 특징으로 새로운 특징 만들기

신경망에서 가장 일반적으로 사용되는 연산은 특징의 가중합을 구하는 것이다. 이 연산은 각 특징에 대한 가중치를 조절하여 기존 특징들을 조합해 새로운 특징을 만든다. 가중합은 각 특징에 대한 가중치 벡터와 데이터 벡터의 점곱으로 간단히 표현할 수 있다.

09.1 수식

수학적으로 보면, 가중치 벡터 WW는 다음과 같이 정의된다:

W=[w1w2⋮wn]W = \begin{bmatrix} w_1 \\ w_2 \\ \vdots \\ w_n \end{bmatrix}

이 때, 가중합 연산은 다음과 같이 정의된다:

N=v(X,W)=X⋅W=x1⋅w1+x2⋅w2+…+xn⋅wnN = v(X, W) = X \cdot W = x_1 \cdot w_1 + x_2 \cdot w_2 + \ldots + x_n \cdot w_n

여기서 XX는 각 특징에 대한 데이터 벡터이다. 이 연산은 사실 행렬곱의 특수한 경우로, XX는 한 개의 행을 가지고, WW는 한 개의 열을 가진다. 이 연산을 통해 각 특징에 대한 가중치를 적용하여 새로운 특징을 생성한다.

09.2 다이어그램


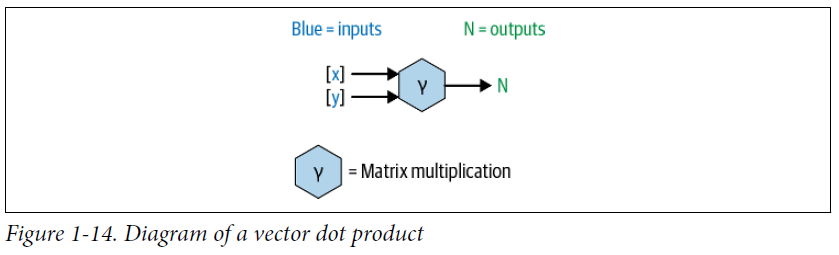
ndarray 객체 두 개를 입력받아 한 개의 ndarray 객체를 출력한다.
생략된 연산을 모두 표현아면 아래와 같다.

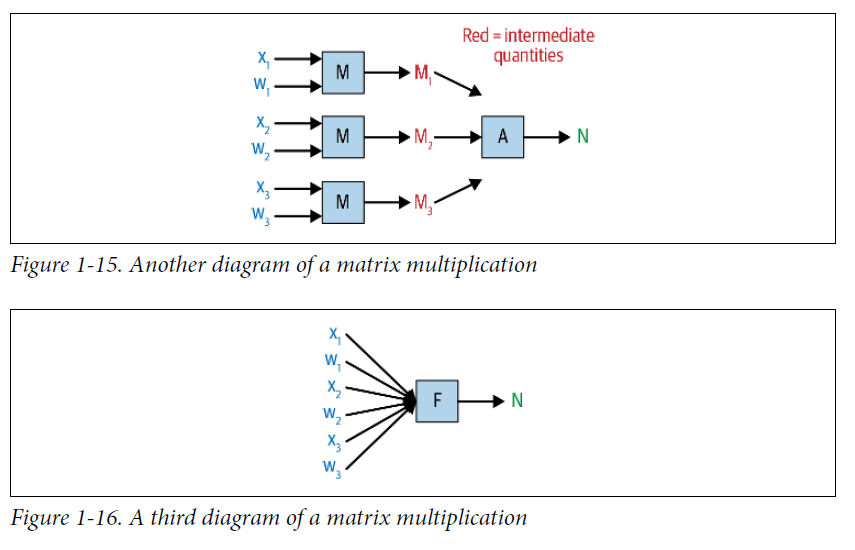
핵심은 dot product(혹은 행렬곱)이 각각의 입력값에 대한 많은 수의 연산을 요약한 것이라는 점이다.

10. 여러 개의 벡터 입력을 갖는 함수의 도함수

10.1 다이어그램

10.2 수식

10.3 코드

11. 벡터 함수와 도함수

11.1 다이어그램

11.2 수식

11.3 코드

12. 두 개의 2차원 행렬을 입력받는 계산 그래프

12.1 수식

12.2 다이어그램

12.3 코드

13. 역방향 계산

13.1 다이어그램

13.2 수식

13.3 코드

profile
민서
CS&ICE, Senior in The Catholic University of Korea. welcome to my page:D http://about.minseo.me/
다음 포스트

Loss function(torch.nn)

0개의 댓글

관련 채용 정보