Digital Building Block
게이트, 멀티플렉서, 디코더, 레지스터, 연산회로, 카운터, 메모리 배열, 논리 배열 등 디지털 시스템 설계의 기본 구성요소를 말한다.
Adder
먼저 1-bit adder를 살펴보자
Half-Adder
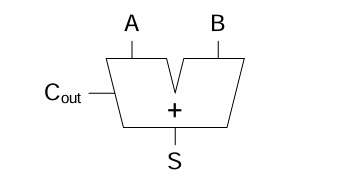
1-bit 이진수 두개(A,B)를 입력 받아 합(S)과 자리 올림(Cout)을 출력하는 회로이다.
| A B | C_out S |
|------|----------|
| 0 0 | 0 0 |
| 0 1 | 0 1 |
| 1 0 | 0 1 |
| 1 1 | 1 0 |
Boolean equation :
S=A⊕B
Cout=AB
carry-in 처리가 불가능하기 때문에 실제 연산회로에서는 잘 사용되지 않는다.
Full adder

1-bit 이진수 두개(A,B)와 이전 연산의 올림(Cin)을 입력으로 받아 합(S)과 자리 올림(Cout)을 출력하는 회로이다. 우리가 주로 사용할 adder의 형태다.
| C_in A B | C_out S |
|------------|----------|
| 0 0 0 | 0 0 |
| 0 0 1 | 0 1 |
| 0 1 0 | 0 1 |
| 0 1 1 | 1 0 |
| 1 0 0 | 0 1 |
| 1 0 1 | 1 0 |
| 1 1 0 | 1 0 |
| 1 1 1 | 1 1 |
Boolean equation :
S=A⊕B⊕Cin (세 비트 중 1이 홀수 개이면 1)
Cout=AB+ACin+BCin (세 비트 중 최소 2개가 1이면 1)
이 것이 adder 설계의 기본 구조이다. 이제 이를 1-bit에서 multibit으로 확장시켜보자.
Multibit Adder
multibit adder는 carry의 처리 방식에 따라 타입이 나뉜다.
간략하게 살펴보면 다음과 같다.
- Ripple-carry (느림)
- Carry-lookahead (빠름)
- Prefix (더 빠름)
블록이 커질 수록 carry-lookahead adder와 prefix adder가 더 빠르게 작동하지만 그만큼 더 많은 하드웨어를 요구한다.
multibit adder의 심볼은 다음과 같다.
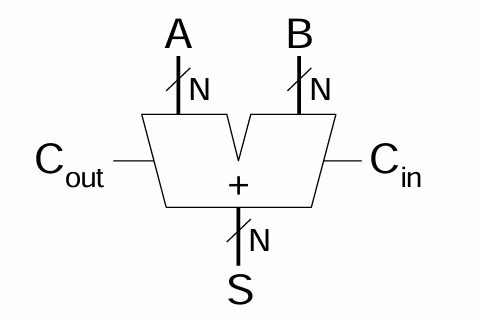
Ripple-Carry Adder
1-bit adder들을 연결하여 구현한다.
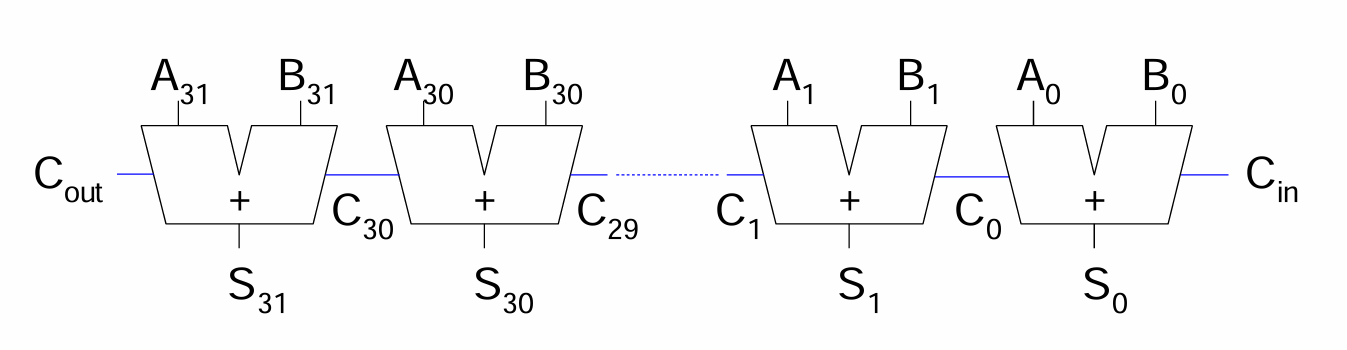
carry가 전체 체인을 타고 나아가기 때문에 Ripple-Carry라고 부른다.
구현이 쉽지만 느리다는 단점이 존재한다.
Ripple-Carry adder의 딜레이는 다음과 같이 계산된다.
tripple=NtFA
N : adder 개수
tFA : 1-bit full adder의 딜레이
Carry-Lookahead Adder
Cout을 generate(생성)와 propagate(전파) 신호를 이용해 계산한다.
쉽게 생각하면 우리가 종이에 연필을 가지고 하는 덧셈 계산 방식과 유사하게 작동한다.
4-bit 이진수 두 개를 가지고 합 연산을 한다고 가정하자.
각 자리 수를 열로 생각할 때, 각 열은 올림을 생성하거나 전파 받을 수 있다.
-
Generate
i 번째 열의 계산은 Ai와 Bi가 모두 1일 때 반드시 Cout을 "생성"한다.
Gi=AiBi
G 계산에 Cin은 고려하지 않는다.
-
Propagate
Ai와 Bi 중 적어도 하나가 1일 경우 Cin을 통해 들어온 carry를 Cout으로 "전파"한다.
Pi=Ai+Bi
-
Carry out
따라서 column i의 Cout은 다음과 같이 계산된다.
Ci=Gi+PiCi−1
두 4-bit 이진수 A3:0=1011, B3:0=0110를 예시로 보면
1011
+0110
-----
0001
P3,P2,P1,P0 = 1,1,1,1
G3,G2,G1,G0 = 0,0,1,0
C3,C2,C1,C0 = 1,1,1,0
이제 이 계산을 열 단위가 아닌 블록 단위로 확장한다.
블록 하나의 크기가 4-bit일 때 Block propagate signal은 다음과 같다.
P3:0=P3P2P1P0
앞서 든 예시에서 P3:0=1이다.
블록에서 캐리는
column 3에서 생성(G)되거나,
column 2에서 생성된 후 column 3에 전파(P)되거나,
column 1에서 생성된 후 column 2와 3에 전파되거나,
column 0에서 생성된 후 column 1, 2, 3에 전파될 경우 발생한다.
G3:0=G3+G2P3+G1P2P3+G0P1P2P3,
즉, G3:0=G3+P3{G2+P2(G1+G0P1)} 이다.
앞서 든 예시에서 G3:0=1이다.
이에 따라서 캐리는
C3=G3:0+P3:0C−1 이다.
4-bit adder block을 이용해 32-bit 구현된 32-bit carry-lookahead adder는 다음과 같다.
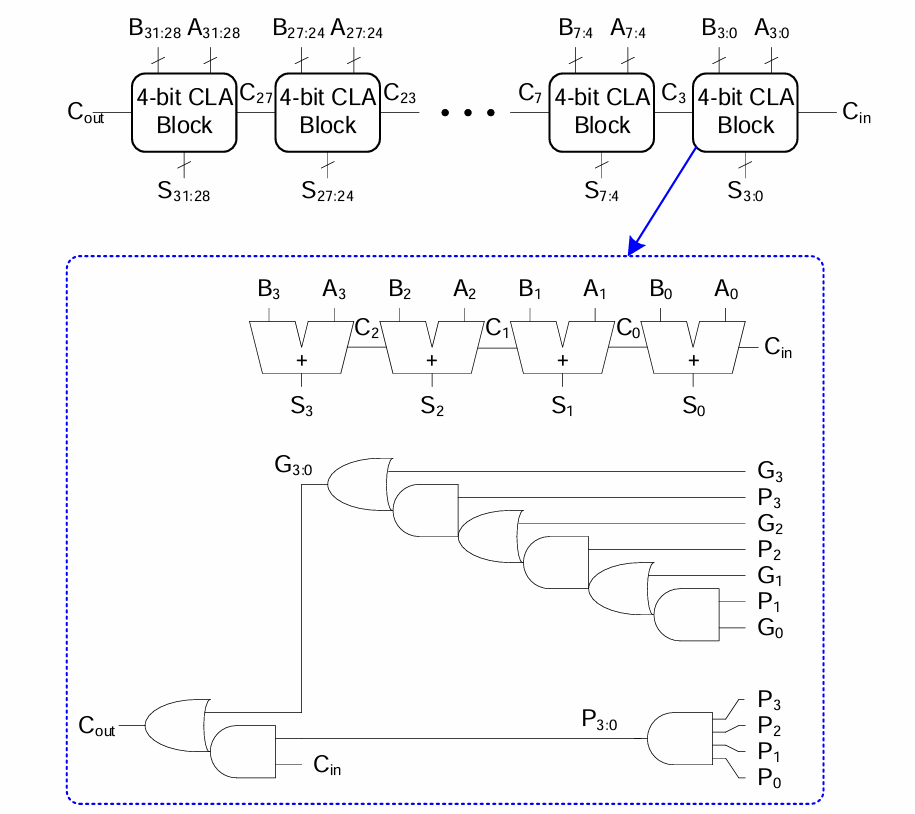
- 모든 열에 대해 Gi와 Pi를 계산한다.
- k-bit 블록에 대한 G와 P를 계산한다.
- 합 계산을 수행하는 동안 Cin이 k-bit의 전파/생성 로직을 통해 전파된다.
- most significant k-bit에 대한 합을 계산한다.
k-bit block으로 구성된 N-bit carry-lookahead adder의 딜레이는 다음과 같이 계산된다.
tCLA=tpg+tpg_block+(kN−1)tAND_OR+ktFA
tpg : 모든 Pi, Gi를 구하는데 걸리는 시간
tpg_block : 모든 Pi:j, Gi:j를 구하는데 걸리는 시간
tAND_OR : k-bit block에 있는 마지막 AND/OR 게이트를 통과하는데 걸리는 시간
Prefix Adder
각 열의 Cin(=Ci−1)을 계산한 후 다음과 같이 sum 한다.
Si=(Ai⊕Bi)⊕Ci−1
Ci−1은 다음 식으로 알아낼 수 있다.
Ci=Gi−1
예: 4-bit block일 경우)
C3=G3:0+P3:0C−1
G3:0=G3+G2P3+G1P2P3+G0P1P2P3
P3:0=P3P2P1P0
C3=G3+G2P3+G1P2P3+G0P1P2P3+P3P2P1P0C−1
C−1=G−1 이므로
C3=G3+G2P3+G1P2P3+G0P1P2P3+G−1P3P2P1P0
∴C3=G3:−1
log2N개의 단계를 통해 sum을 구할 수 있다.
column -1은 Cin을 갖고 있다. 그러므로
G−1=Cin, P−1=X (not used)
column i의 Cin은 column i−1의 Cout이다.
Ci−1=Gi−1:−1
그 결과로 sum을 실행한다.
Si=(Ai⊕Bi)⊕Gi−1:−1
따라서 이 계산법의 목표는 모든 block의 generate(G0:−1,G1:−1,G2:−1,...=C0,C1,C2,...)를 빠르게 계산하는 것이다.
block generate/propagate 시그널은 하위 block의 시그널로 표현할 수 있음을 기억하자.
Gi:j=Gi:k+Pi:kGk−1:j
Pi:j=Pi:kPk−1:j
즉, block i:j는 상위 부분(i:k)에서 carry(Gi:k)를 생성하거나, 하위 부분(k−1:j)에서 carry(Gk−1:j)를 생성하고 상위 부분에서 전파(Pi:k)될 경우 generate signal(Gi:j)을 발생시킨다.
또한 상위 부분과 하위 부분 모두 전파될 경우(Pi:k AND Pk−1:j) propagate signal(Pi:j)을 발생시킨다.
<prefix adder 예시>
A=10102, B=01112
1010
+0111
------
10001
G3,G2,G1,G0,G−1=0,0,1,0,0
P3,P2,P1,P0,P−1=1,1,1,1,X
G2:−1=G2:1+P2:1G0:−1
G2:1=G2+P2G1=0+1⋅1=1
∴G2:−1=1
G1:−1=G1:0+P1:0G−1
G1:0=G1+P1G0=1+1⋅0=1
∴G1:−1=1
G0:−1=G0+P0G−1=0+1⋅0=0
S3=(A3⊕B3)⊕G2:−1=(1⊕0)⊕1=1⊕1=0
S2=(A2⊕B2)⊕G1:−1=(0⊕1)⊕1=1⊕1=0
S1=(A1⊕B1)⊕G0:−1=(1⊕1)⊕0=0⊕0=0
S0=(A0⊕B0)⊕G−1=(0⊕1)⊕0=1⊕0=1
∴S=00012
16-bit prefix adder는 다음과 같이 구현된다.
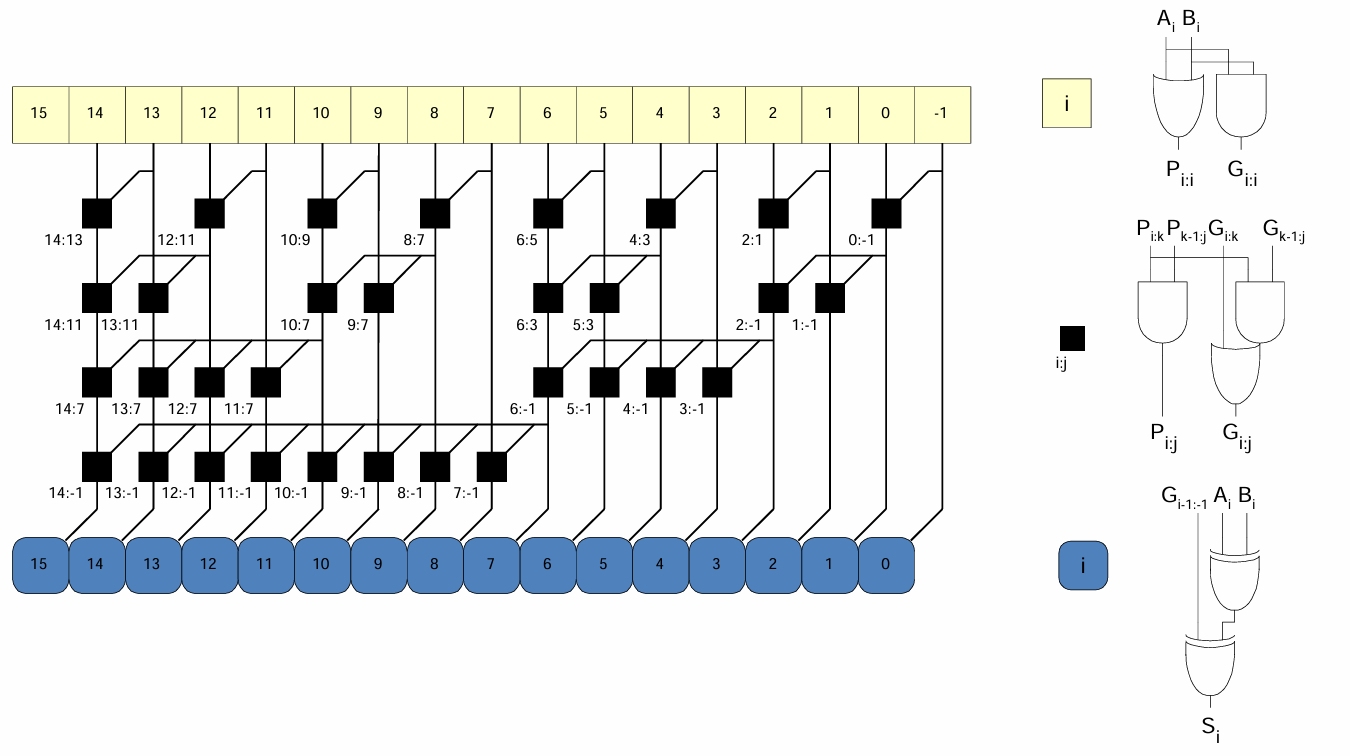
컴퓨터 알고리즘 중 분할정복과 비슷한 원리로 이해할 수 있다.(이건 하드웨어지만)
딜레이는 다음과 같다.
tPA=tpg+log2N(tpg_prefix)+tXOR
tpg : Pi, Gi 계산에 걸리는 시간
tpg_prefix : 위 회로도에서 검은색으로 표시된 prefix 셀의 딜레이
이쯤에서 정리를 한 번 해보자.
Adder summary
| Half adder | Full-adder |
|---|
| 입력 | A, B | A, B, Carry-in |
| 출력 | Sum, Carry-out | Sum, Carry-out |
-
Full-Adder 설계 기본 구조
Si=Ai⊕Bi⊕Cin
-
multibit adder
| 타입 | 방식 | 딜레이 |
|---|
| Ripple-Carry | 1-bit full adder를 직렬로 연결하여 carry를 순차적으로 전파 | tripple=NtFA |
| Carry-Lookahead | 각 자리의 P와 G 신호를 미리 계산하여 carry를 병렬로 처리 | tCLA=tpg+tpg_block+(kN−1)tAND_OR+ktFA |
| Prefix | 각 자리의 Carry-in을 prefix 셀로 빠르게 계산 | tPA=tpg+log2N(tpg_prefix)+tXOR |
Cin을 어떻게 계산하느냐에 차이가 있다.
딜레이 계산 예제
32-bit ripple-carry, CLA, prefix adder의 딜레이를 비교하여라.
<조건>
CLA는 4-bit block들로 구성되었다.
2-input 게이트들의 딜레이는 100ps,
full adder의 딜레이는 300ps이다.
tripple=NtFA=32×300 (ps)=9.6ns
tCLA=tpg+tpg_block+(kN−1)tAND_OR+ktFA=100+100×6+(432−1)×100×2+4×300=100+600+1400+1200 (ps)=3.3ns
tPA=tpg+log2N(tpg_prefix)+tXOR=100+log232×200+100 (ps)=1.2ns
tripple>tCLA>tPA
Subtracter
Subtracter의 기반은 adder다.
이진수 −B=B+1임을 이용한다.
A−B=A+B+1
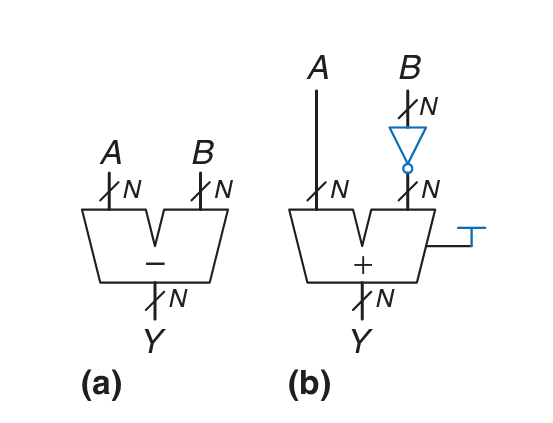
(a) subtracter symbol, (b) implementation
Equality comparator
두 개의 n-bit 이진수가 같은지(A=B) 판별한다.
각 자리수마다 XNOR연산을 수행하여 AND 게이트를 통해 하나의 output을 낸다.
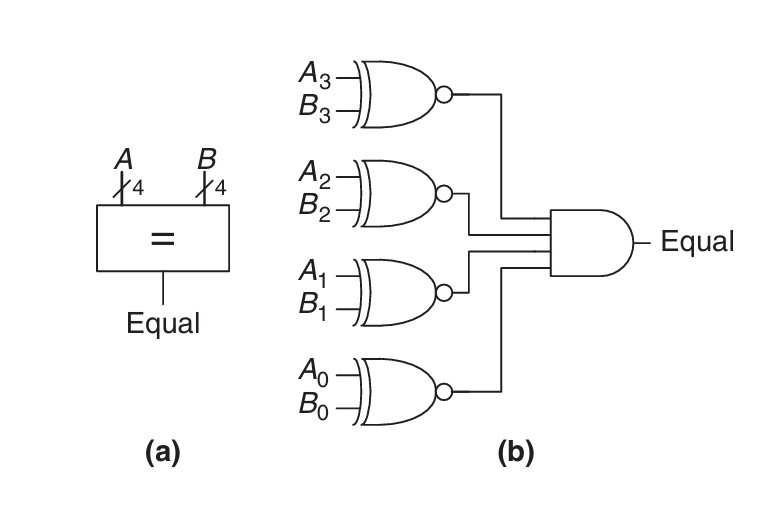
Signed Less Than comparator
대소비교(A<B)는 A−B연산을 사용한다.
A−B의 결과가 음수일 경우 A<B이다.
오버플로우에 주의해야한다.
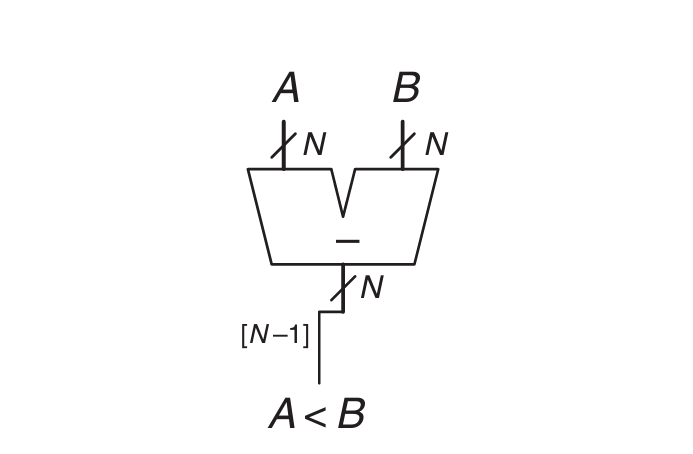
signed만 판별하면 되기 때문에 연산 결과의 msb만 사용한다.
<참고자료>
Harris & Harris, Digital Design and Computer Architecture, RISC-V Edition, 2022.









