Background

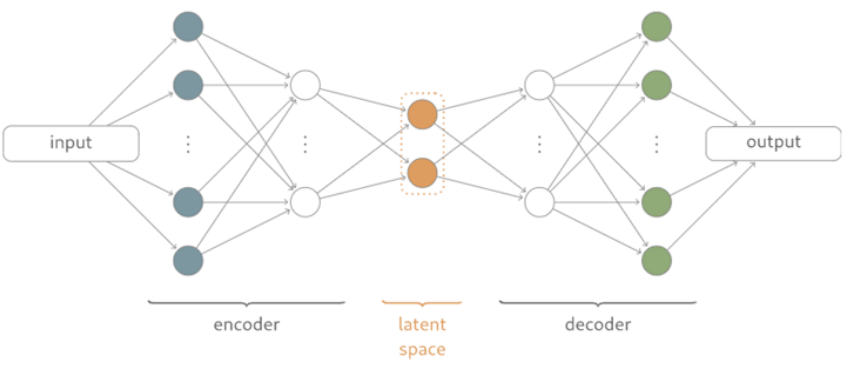
AutoEncoder

• Encoder 와 Decoder로 구성된 딥러닝 모델을 의미한다.

• input 과 output 출력의 크기가 동일하다.

• 가장 핵심은 데이터를 잘 압축하는 latent space vector를 얻고자 하는 것이다.
  
  출처: https://itsnyeong.tistory.com/13

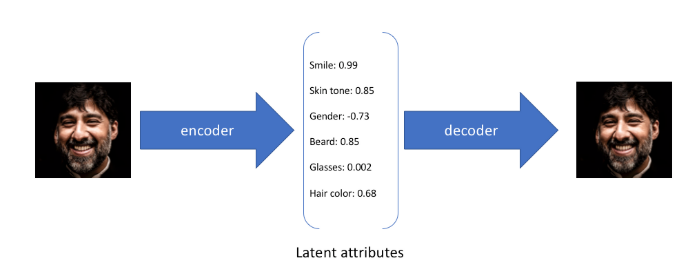latent space vector의 값을 조정하여 입력값을 다양한 형태로 변환이 가능해진다.
출처: https://itsnyeong.tistory.com/13

AutoEncoder의 활용도

Denoising

• 이미지의 노이즈를 제거하는데 사용된다.

• 노이즈가 있는 이미지를 AutoEncoder를 통해 변환하면 노이즈가 제거된 이미지를 생성한다.
  

AutoEncoder 손실함수

• AutoEncoder의 손실함수는 MSE(Mean Square Error)함수를 사용하여 오차역전파를 계산을 진행한다.

• 입력값과 AutoEncoder를 통해서 생성된 출력값의 차이가 최소화 되도록 학습한다.

• 하지만 MSE 값이 작다고 해서 이미지가 더 잘 생성한다고 하기는 어렵다.

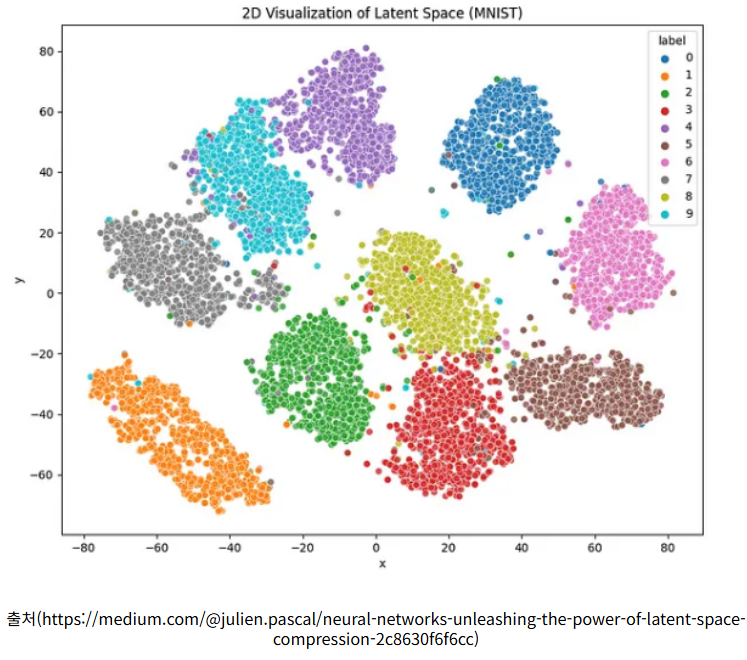
latent vector & latent space

• latent vector는 dataset의 하나의 데이터 샘플이 갖는 hidden 벡터 형태의 변수이고, 그것들이 모여 분포 형태를 이루는것을 latent space를 형성한다.

• latent vector는 데이터를 설명하는 하나의 feature이고 latent space는 데이터를 가장 잘 설명할 수 있는 feature들의 모임을 의미한다.

• 예를 들어 강아지 이미지의 픽셀에 대한 모든 부분은 '강아지'를 표현하지 않지만 latent vector들을 추출하고 latent space를 본다면 결국 '강아지'를 표현하는 것으로 볼수있다.

PyTorch 구현코드: https://github.com/namduhus/AutoEncoder

Bayes Decision Theory

설명: https://process-mining.tistory.com/81

VAE: Auto-Encoding Variational Bayes

https://arxiv.org/pdf/1312.6114

Author: Diederik P. Kingma, Max Welling

Abstract

• 본 논문은 다루기 힘든 사후 분포와 대규모 데이터 세트가 있는 연속 잠재 변수가 있는 상황에서 방향성 확률 모델에서 효율적인 추론과 학습을 어떻게 수행할 수 있을까? 란 질문에서 시작된다.

• 우리는 큰 데이터셋에도 확장할 수 있고 가벼운 미분가능성 조건이 있다면 계산이 불가능한 경우에도 작동하는 stochastic variational inference and learning 알고리즘을 제안한다.

• 첫째, variational lower bound의 reparameterization이 표준적인 stochastic gradient 방법론들을 사용하여 직접적으로 최적화될 수 있는 lower bound estimator를 만들어낸다는 것을 보였다.

• 둘째, 각 datapoint가 연속형 잠재 변수를 가지는 i.i.d.(독립항등분포) 데이터셋에 대해서, 제안된 lower bound estimator를 사용해 approximate inference model(또는 recognition model이라고 불림)을 계산이 불가능한 사후확률에 fitting 시킴으로써 사후 추론이 특히 효율적으로 만들어질 수 있다는 점을 보인다.

Introduction

• VB(variational Bayesian) 접근 방식은 다루기 힘든 사후확률에 대한 근사의 최적화를 포함한다. 불행히도 일반적인 mean-field 접근 방식은 대략적인 사후확률에 대한 기댓값의 분석적 해를 요구하며, 일반적인 경우에 이 또한 계산 불가능하다.

• 논문에서는 variational lower bound의 reparameterization가 lower bound의 단순한 미분 가능한 편향되지 않은 추정치를 산출하는 방법을 보여준다.

• 이 SGVB(Stochastic Gradient Variational Bayes) estimator는 연속형 잠재 변수나 파라미터를 가지는 어떤 모델에서도 효율적인 근사 사후추론를 위해 사용될 수 있으며, 표준 gradient ascent 기법을 사용해서 직접적으로 최적화한다.\

• AEVB 알고리즘에서 우리는 SGVB 추정기를 사용하여 인식 모델을 최적화함으로써 추론 및 학습을 특히 효율적으로 만든다. 이 모델을 사용하면 간단한 샘플링을 사용하여 매우 효율적인 근사 사후 추론을 수행할 수 있다. 학습된 근사 사후 추론 모델은 인식, 잡음 제거, 표현 및 시각화 목적과 같은 다양한 작업에도 사용할 수 있다.

VAE Goal

• VAE는 오토인코더와 목적이 전혀 다르다. 오토인코더는 어떤 데이터를 잘 압축하고 특징을 잘 뽑는지의 관한 Encoder에 중점을 둔 모델이고, VAE는 Generation model로 어떤 새로운 데이터를 잘 만들어 내는지에 관한 Decoder에 중점을 둔 모델이다.

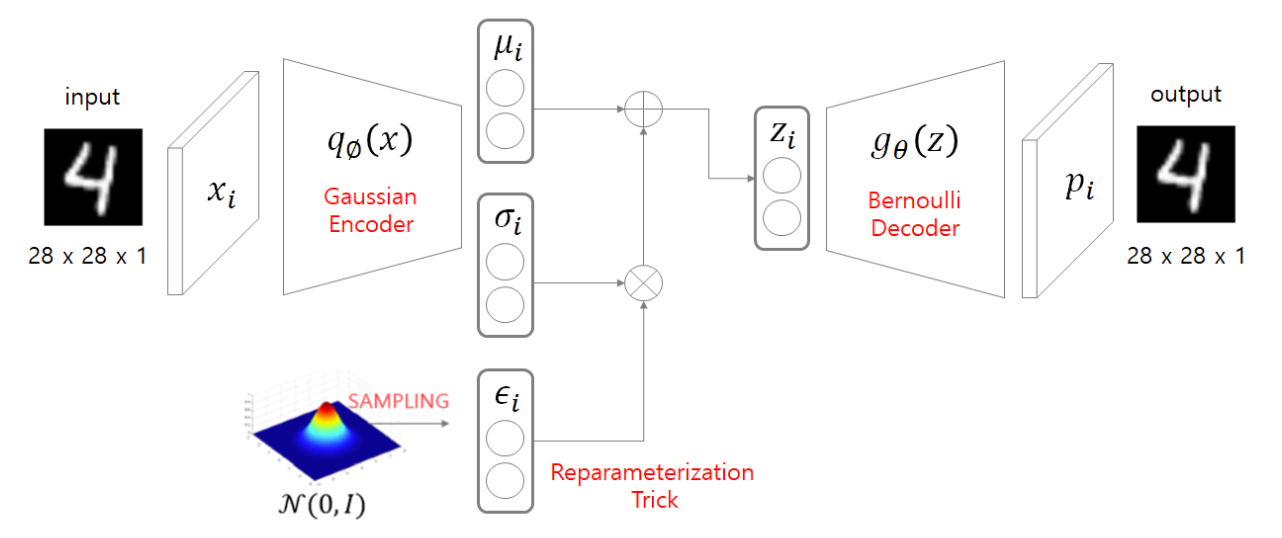
VAE Structure

• 데이터가 Encoder를 통과하면 평균(뮤)와 표준편차(시그마) 두개의 값을 output으로 한다.

• 평균과 표준편차를 알면 정규분포를 만들수 있고, 이 분포에서 z를 샘플링하고 Decoder를 통과하여 input과 비슷한 분포를 가진 데이터를 생성할 수 있다.

• 하지만 Sampling은 랜덤성을 띄기 때문에 계산이 불가능한데, 이를 Reparameterization Trick을 사용하여 미분이 가능하게 만든다.

Reparameterization Trick

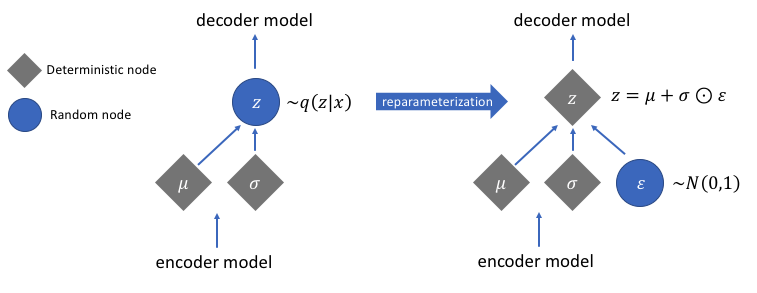
• VAE에서 쓰는 방법이 Encoder를 통과하면 평균(뮤) 와 표준편차(시그마)를 뽑고 그것을 이용해서 정규 분포를 만들어서 Sampling을 해서 z를 만드는 것이다.

• 하지만 이 방법은 미분이 불가능하기 때문에, 평균이 0이고 표준편차가 1인 표준정규분포에서 E를 샘플링한 뒤, 그것을 표준편차에 곱해주고 평균에 더해주면 새로운 Sampling 값이 된다.

Loss Fuction

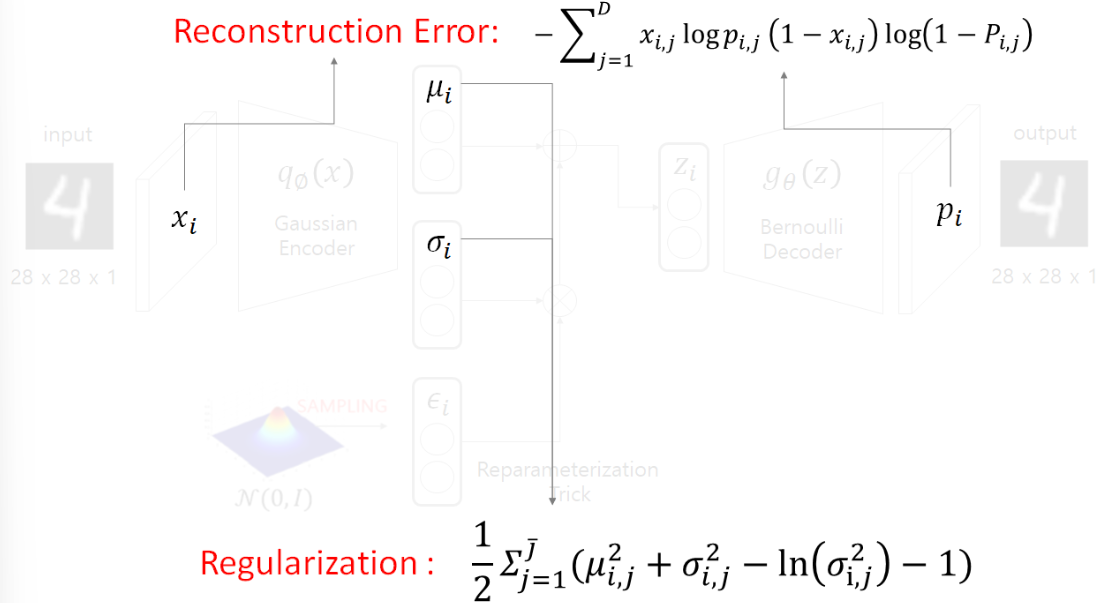
• VAE에서는 손실함수가 2개이고, 2개의 합으로 나타내어 진다.

• Reconstruction Error는 확률을 정규분포로 가정하냐, 베르누이로 가정하냐에 따라 2가지가 있다.

• 본 논문에서는 베르누이로 가정하여서 $Cross Entropy Loss$로 정의를 했다.

Loss Function 배경

• 입력데이터의 분포를 근사하는 모델을 생성하는 것이다.

• 출력값이 있을 때 우리가 원하는 정답인 $x$가 나올 확률이 높길 바라는 것이라고 할 수 있다.

• 따라서 $x$의 가능도(likelihood)를 최대화 하는 확률 분포를 만들고 싶은 것이 목적이 된다.

ELBO

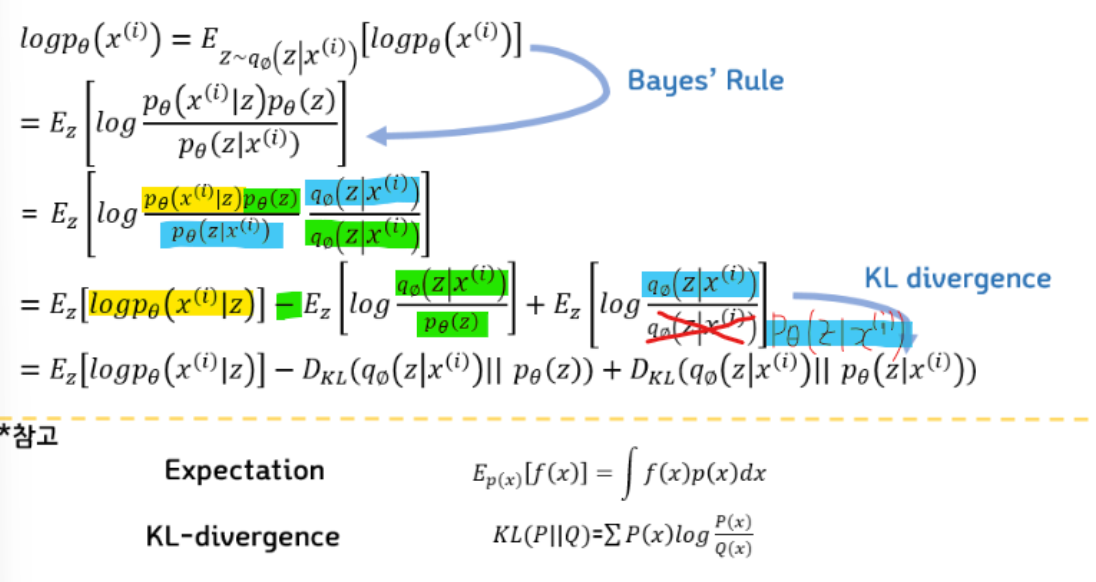
• $p(x)$를 최대화 시키는 것이 목표이다.

• 첫번째 줄에서는 계산을 쉽게 하기위해서 $p(x)$에 $log$ 를 씌우고 기대값 형태로 나타낸다. 기대값은 $z$가 Encoder를 거져서 나오는 확률 분포를 따를 때의 기대값이다.

• 두번째 줄에서는 베이즈 정리를 이용해서 식을 변경한다.

• 세번째 줄에서는 분모분자에 같은 값을 곱해서 $log$안의 분수를 덧셈 뺄셈 형태로 변환한다.

• 4번째 줄에서는 수식이 KLD와 형태가 같기 때문에 KLD로 바꿔주면 최종 식이 된다.

ELBO 최종 목표

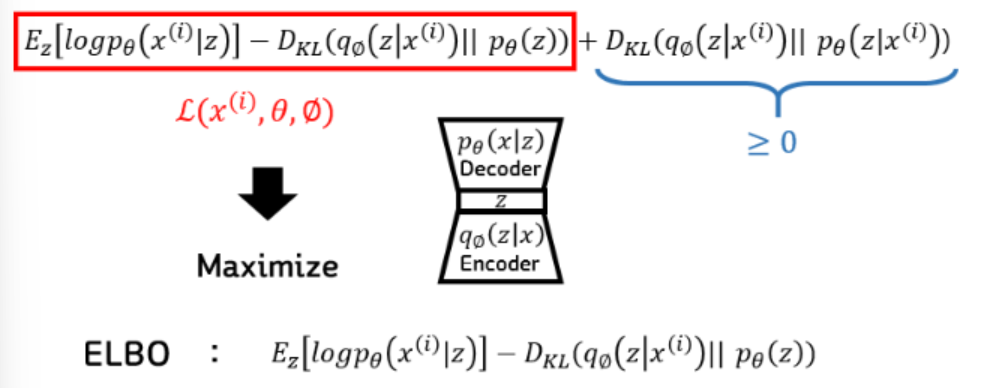
• 맨 뒤의 수식을 최소화하는 것인데, 여기에서도 $p(z|x)$의 값은 구할 수 없다.

• $x$가 주어졌을 때, $z$의 true 값을 알 수 없기 때문이다.

• 이 식이 KLD라는 것을 알고 항상 0보다 크거나 같다는 정도는 알기 때문에, 앞의 부분을 Lower Bound로 해서 최대화를 시켜주면 전체 식을 최대화 한것과 같다는 결론이 나온다.

• 베이즈 정리에서 Evidence에 해당되는 $x$에 대한 확률(Marginal Likelihood)을 구하는 것이기 때문에 Evidence LowerBOund 라고 해서 ELBO라고 불린다.

Regularization 계산

설명: https://dongju923.github.io/paper/VAE/#reconstruction-error-%EA%B3%84%EC%82%B0