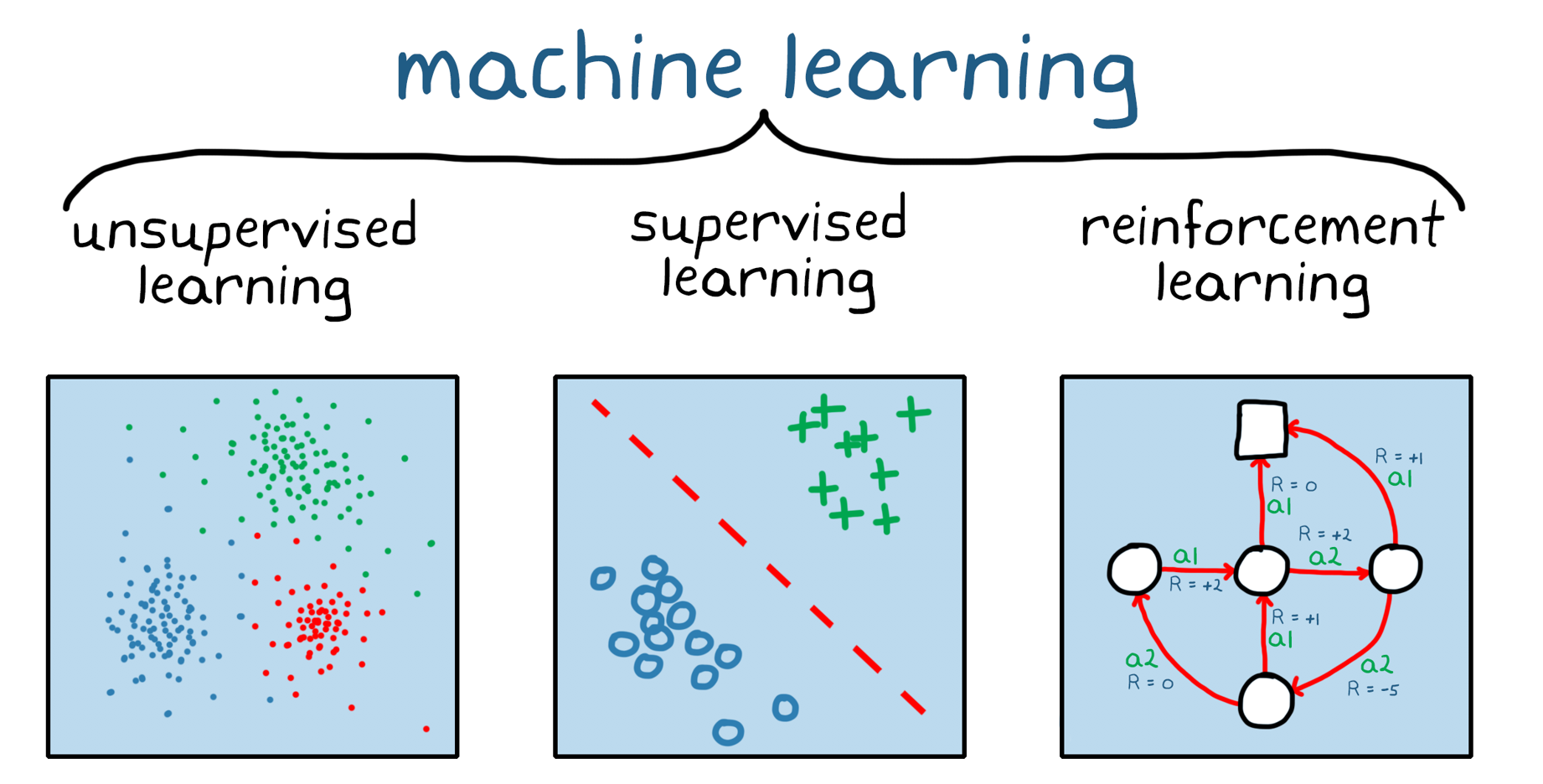
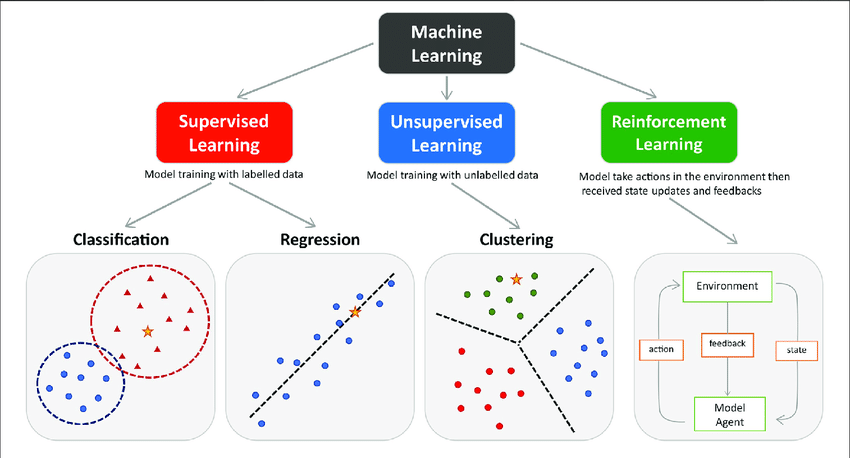
1. 회귀분석이란?

회귀분석은 독립변인(x)이 종속변인(y)에 영향을 미치는지 알아보고자 할 때 실시하는 분석방법이다.
단순 선형 회귀분석은 독립변수 X(설명변수)에 대하여 종속변수 Y(반응변수)들 사이의 관계를 수학적 모형을 이용하여 규명하는 것이다.
규명된 함수식을 이용하여 설명변수들의 변화로부터 종속변수의 변화를 예측하는 분석이다.

예를 들어, 대학운동부 학생들의 신체검사 자료 (아래 그래프)가 있다.
신입생 A가 들어왔다. (키는 175cm이다) 예상 몸무게는?

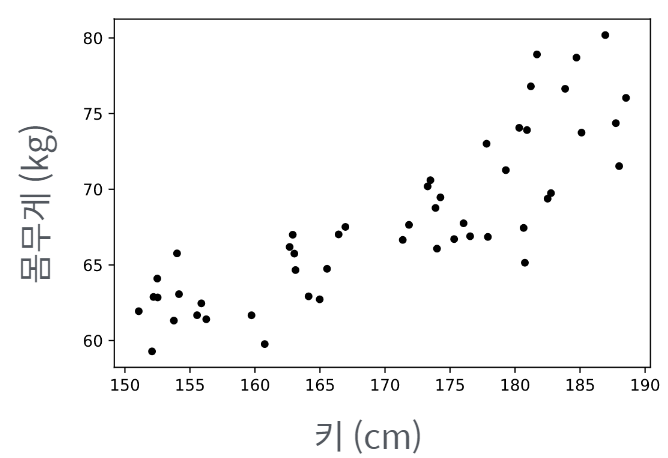
위 그래프에서 아래와 같이 빨간 직선을 그을 수 있게 되는데,

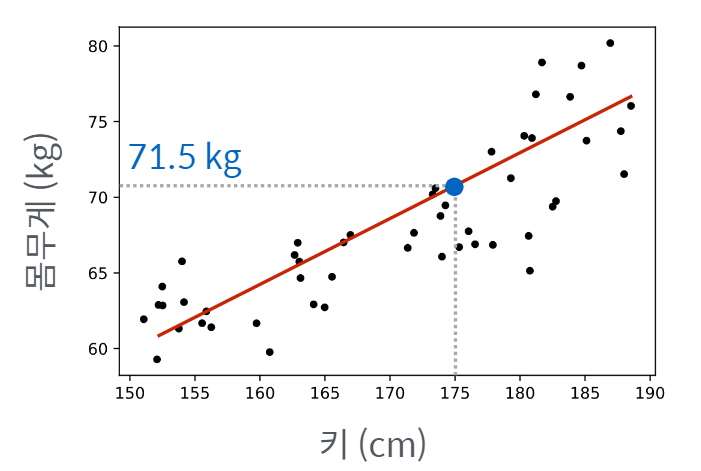
이를 통해 예측 할 수 있는 175cm의 몸무게는 71.5kg가 된다.

즉, 주어진 데이터를 통해 목표값을 예측하기 위해 "데이터를 가장 잘 설명하는 어떠한 직선을 하나 찾는 것" 이 "회귀분석법"이다.

1-1. 기울기와 절편

위의 설명에서 언급했듯, 최적의 직선을 구하기 위해서는 "기울기"와 "절편"을 구해야 한다.
즉, 단순 선형 회귀 분석 수식
$y^{(i)} \sim \beta_0 x^{(i)} + \beta_1$ 의 $\beta_0$, $\beta_1$을 구하는 과정이다.

import matplotlib as mpl
mpl.use("Agg")
import matplotlib.pyplot as plt
import numpy as np

# 실습에 필요한 데이터입니다. 수정하지마세요. 
X = [8.70153760, 3.90825773, 1.89362433, 3.28730045, 7.39333004, 2.98984649, 2.25757240, 9.84450732, 9.94589513, 5.48321616]
Y = [5.64413093, 3.75876583, 3.87233310, 4.40990425, 6.43845020, 4.02827829, 2.26105955, 7.15768995, 6.29097441, 5.19692852]

beta_0 = 0.65   # beta_0에 저장된 기울기 값을 조정해보세요. 
beta_1 = 0.85 # beta_1에 저장된 절편 값을 조정해보세요.

plt.scatter(X, Y) # (x, y) 점을 그립니다.
plt.plot([0, 10], [beta_1, 10 * beta_0 + beta_1], c='r') # y = beta_0 * x + beta_1 에 해당하는 선을 그립니다.

plt.xlim(0, 10) # 그래프의 X축을 설정합니다.
plt.ylim(0, 10) # 그래프의 Y축을 설정합니다.

# 엘리스에 이미지를 표시합니다.
plt.savefig("test.png")

2. 모델의 학습목표

$y^{(i)} \sim \beta_0 x^{(i)} + \beta_1$

각 데이터 $(x^{(i)}, y^{(i)})$의 실제값과 모델이 예측하는 값을 최소한으로 하는 것이 선형회귀모델의 학습 목표!!

i번째 데이터 $(x^{(i)}, y^{(i)})$에 대해 :
- 실제값 : $y^{(i)}$
- 예측값 : $\beta_0 x^{(i)} + \beta_1$
- 차이 : $y^{(i)} - (\beta_0 x^{(i)} + \beta_1)$
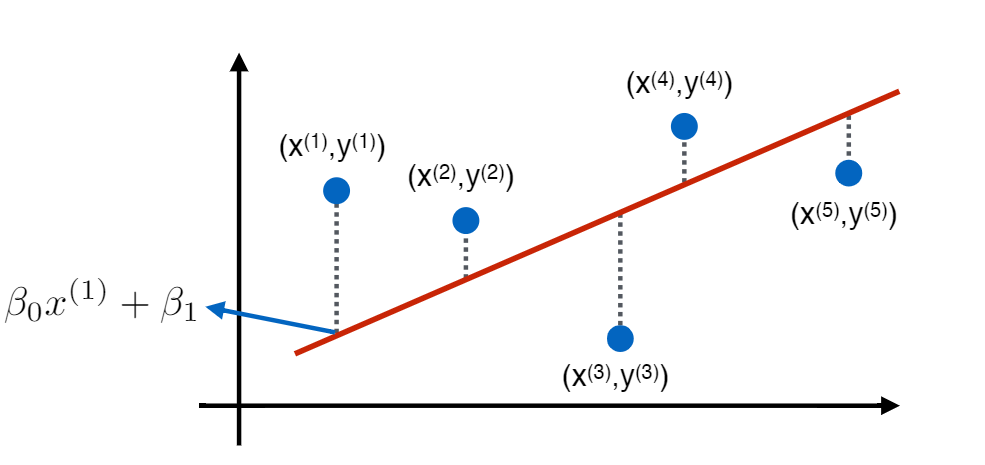
- 전체 모델의 차이 : $\displaystyle\sum_{i}^{N} (y^{(i)} - (\beta_0 x^{(i)} + \beta_1))$

그런데, 단순히 $\Sigma$를 취하면, 차이가 + / - 가 더해지면서 0이 될 수도 있음.
이를 보완하기위해 $\displaystyle\sum_{i}^{N} (y^{(i)} - (\beta_0 x^{(i)} + \beta_1))^2$을 통해 전체 모델의 차이를 최소로 하는 $\beta_0, \beta_1$ 을 구하게 된다.
또한, 이 전체 모델의 차이를 Loss function이라고 부른다.

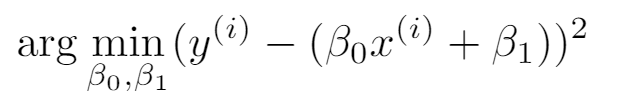
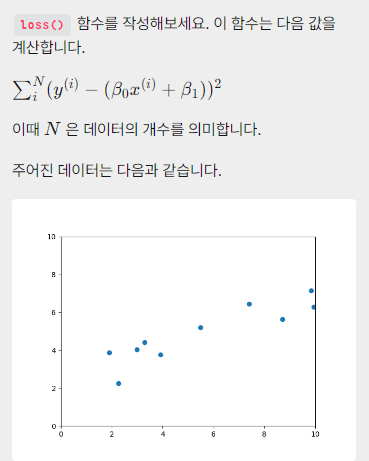
2-1. Loss function 코드로 구현하기

import matplotlib as mpl
mpl.use("Agg")
import matplotlib.pyplot as plt
import numpy as np

def loss(x, y, beta_0, beta_1):
    N = len(x)
    
    '''
    x, y, beta_0, beta_1 을 이용해 loss값을 계산한 뒤 리턴합니다.
    '''
    x=np.array(x)
    y=np.array(y)
    y_predict = beta_0*x + beta_1
    total_loss = np.sum((y- y_predict)**2)
    return total_loss

X = [8.70153760, 3.90825773, 1.89362433, 3.28730045, 7.39333004, 2.98984649, 2.25757240, 9.84450732, 9.94589513, 5.48321616]
Y = [5.64413093, 3.75876583, 3.87233310, 4.40990425, 6.43845020, 4.02827829, 2.26105955, 7.15768995, 6.29097441, 5.19692852]

beta_0 = 1 # 기울기
beta_1 = 0.5 # 절편

print("Loss: %f" % loss(X, Y, beta_0, beta_1))

plt.scatter(X, Y) # (x, y) 점을 그립니다.
plt.plot([0, 10], [beta_1, 10 * beta_0 + beta_1], c='r') # y = beta_0 * x + beta_1 에 해당하는 선을 그립니다.

plt.xlim(0, 10) # 그래프의 X축을 설정합니다.
plt.ylim(0, 10) # 그래프의 Y축을 설정합니다.
plt.savefig("test.png") # 저장 후 엘리스에 이미지를 표시합니다.
eu.send_image("test.png")

2-2. Scikit-learn을 이용한 회귀분석

import matplotlib as mpl
mpl.use("Agg")
import matplotlib.pyplot as plt
import numpy as np
from sklearn.linear_model import LinearRegression

import elice_utils
eu = elice_utils.EliceUtils()

def loss(x, y, beta_0, beta_1):
    N = len(x)
    x = np.array(x)
    y = np.array(y)
    y_predict = beta_0 * x + beta_1
    total_loss = np.sum((y - y_predict) ** 2)  
    return total_loss
    
X = [8.70153760, 3.90825773, 1.89362433, 3.28730045, 7.39333004, 2.98984649, 2.25757240, 9.84450732, 9.94589513, 5.48321616]
Y = [5.64413093, 3.75876583, 3.87233310, 4.40990425, 6.43845020, 4.02827829, 2.26105955, 7.15768995, 6.29097441, 5.19692852]

train_X = np.array(X).reshape(-1, 1)
train_Y = np.array(Y)

'''
여기에서 모델을 트레이닝합니다.
'''
lrmodel = LinearRegression()
lrmodel.fit(train_X, train_Y)

'''
loss가 최소가 되는 직선의 기울기와 절편을 계산함
'''
beta_0 = lrmodel.coef_[0]   # lrmodel로 구한 직선의 기울기
beta_1 = lrmodel.intercept_ # lrmodel로 구한 직선의 y절편

print("beta_0: %f" % beta_0)
print("beta_1: %f" % beta_1)
print("Loss: %f" % loss(X, Y, beta_0, beta_1))

plt.scatter(X, Y) # (x, y) 점을 그립니다.
plt.plot([0, 10], [beta_1, 10 * beta_0 + beta_1], c='r') # y = beta_0 * x + beta_1 에 해당하는 선을 그립니다.

plt.xlim(0, 10) # 그래프의 X축을 설정합니다.
plt.ylim(0, 10) # 그래프의 Y축을 설정합니다.
plt.savefig("test.png") # 저장 후 엘리스에 이미지를 표시합니다.
eu.send_image("test.png")

3. 다중회귀분석

선형회귀분석은 독립변수 X(설명변수)가 하나였지만, 다중회귀분석은 독립변수 X가 여러개인 경우이다.
즉, 예를 들어 설명을 하자면

• 데이터 : N개의 FB, TV, 신문 광고 예산과 판매량 (X1, X2, X3 과 Y)
• 목표 : FB, TV, 신문에 각각 얼마씩을 투자했을 때 얼마나 팔릴까?
• 가정 : 판매량은 FB, TV, 신문 광고료와 선형적 관계

$Y \sim \beta_0X_1 + \beta_1X_2 + \beta_2X_3 + \beta_3$

• 실제값 : $y^{(i)}$
• 모델이 예측한 값 : $\beta_0x_1^{(i)} + \beta_1x_2^{(i)} + \beta_2x_3^{(i)} + \beta_3$
• 차이의 제곱 : $(y^{(i)} - (\beta_0x_1^{(i)} + \beta_1x_2^{(i)} + \beta_2x_3^{(i)} + \beta_3))^2$
• 차이의 제곱의 합 : $\displaystyle\sum_{i}^{N}(y^{(i)} - (\beta_0x_1^{(i)} + \beta_1x_2^{(i)} + \beta_2x_3^{(i)} + \beta_3))^2 = Loss function$

이 Loss function을 최소로 하는 $\beta_0, \beta_1, \beta_2, \beta_3$을 구하는 것이다.

3-1. 다중 회귀 분석

import numpy as np
from sklearn.linear_model import LinearRegression
from sklearn.metrics import r2_score

'''
./data/Advertising.csv 에서 데이터를 읽어, X와 Y를 만듭니다.

X는 (200, 3) 의 shape을 가진 2차원 np.array,
Y는 (200,) 의 shape을 가진 1차원 np.array여야 합니다.

X는 FB, TV, Newspaper column 에 해당하는 데이터를 저장해야 합니다.
Y는 Sales column 에 해당하는 데이터를 저장해야 합니다.
'''

import csv
csvreader = csv.reader(open("data/Advertising.csv"))

x = []
y = []

next(csvreader)
for line in csvreader :
    x_i = [ float(line[1]), float(line[2]), float(line[3]) ]
    y_i = float(line[4])
    x.append(x_i)
    y.append(y_i)

X = np.array(x)
Y = np.array(y)

lrmodel = LinearRegression()
lrmodel.fit(X, Y)

beta_0 = lrmodel.coef_[0] # 0번째 변수에 대한 계수 (페이스북)
beta_1 = lrmodel.coef_[1] # 1번째 변수에 대한 계수 (TV)
beta_2 = lrmodel.coef_[2] # 2번째 변수에 대한 계수 (신문)
beta_3 = lrmodel.intercept_ # y절편 (기본 판매량)

print("beta_0: %f" % beta_0)
print("beta_1: %f" % beta_1)
print("beta_2: %f" % beta_2)
print("beta_3: %f" % beta_3)

def expected_sales(fb, tv, newspaper, beta_0, beta_1, beta_2, beta_3):
    '''
    FB에 fb만큼, TV에 tv만큼, Newspaper에 newspaper 만큼의 광고비를 사용했고,
    트레이닝된 모델의 weight 들이 beta_0, beta_1, beta_2, beta_3 일 때
    예상되는 Sales 의 양을 출력합니다.
    '''
    y = beta_0*fb + beta_1*tv + beta_2*newspaper + beta_3
    return y

print("예상 판매량: %f" % expected_sales(10, 12, 3, beta_0, beta_1, beta_2, beta_3))

3-2. 다항식 회귀분석

import numpy as np
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error
from sklearn.model_selection import train_test_split

'''
./data/Advertising.csv 에서 데이터를 읽어, X와 Y를 만듭니다.

X는 (200, 3) 의 shape을 가진 2차원 np.array,
Y는 (200,) 의 shape을 가진 1차원 np.array여야 합니다.

X는 FB, TV, Newspaper column 에 해당하는 데이터를 저장해야 합니다.
Y는 Sales column 에 해당하는 데이터를 저장해야 합니다.
'''
import csv
csvreader = csv.reader(open("data/Advertising.csv")) #예시파일이라 해당 코드에서는 안불러짐

x = []
y = []

next(csvreader)
for line in csvreader :
    x_i = [ float(line[1]), float(line[2]), float(line[3]) ]
    y_i = float(line[4])
    x.append(x_i)
    y.append(y_i)

X = np.array(x)
Y = np.array(y)


# 다항식 회귀분석을 진행하기 위해 변수들을 조합합니다.
X_poly = []
for x_i in X:
    X_poly.append([
        x_i[0] ** 2, # X_1^2
        x_i[1] ** 2,
        x_i[2] ** 2,
        x_i[1], # X_2
        x_i[0],
        x_i[2],
        x_i[1] * x_i[0],
        x_i[1] * x_i[2], # X_2 * X_3
        x_i[0] * x_i[2]
    ])

# X, Y를 80:20으로 나눕니다. 80%는 트레이닝 데이터, 20%는 테스트 데이터입니다.
x_train, x_test, y_train, y_test = train_test_split(X_poly, Y, test_size=0.2, random_state=0)

# x_train, y_train에 대해 다항식 회귀분석을 진행합니다.
lrmodel = LinearRegression()
lrmodel.fit(x_train, y_train)

#x_train에 대해, 만든 회귀모델의 예측값을 구하고, 이 값과 y_train 의 차이를 이용해 MSE를 구합니다.
predicted_y_train = lrmodel.predict(x_train)
mse_train = mean_squared_error(y_train, predicted_y_train)
print("MSE on train data: {}".format(mse_train))

# x_test에 대해, 만든 회귀모델의 예측값을 구하고, 이 값과 y_test 의 차이를 이용해 MSE를 구합니다. 이 값이 1 미만이 되도록 모델을 구성해 봅니다.
predicted_y_test = lrmodel.predict(x_test)
mse_test = mean_squared_error(y_test, predicted_y_test)
print("MSE on test data: {}".format(mse_test))

3-3. 영어 단어 코퍼스 분석하기

import operator
from sklearn.linear_model import LinearRegression
import numpy as np
import matplotlib
matplotlib.use('Agg')
import matplotlib.pyplot as plt
import elice_utils
import csv

def main():
    words = read_data()
    words = sorted(words, key = lambda x : x[1] , reverse = True) # words.txt 단어를 빈도수 순으로 정렬합니다.
    
    
    # 정수로 표현된 단어를 X축 리스트에, 각 단어의 빈도수를 Y축 리스트에 저장합니다.  
    X = list(range(1, len(words)+1))
    Y = [x[1] for x in words]
    
    
    
    # X, Y 리스트를 array로 변환한 후 각 원소 값에 log()를 적용합니다.
    X, Y = np.array(X), np.array(Y)  
    
    X, Y = np.log(X), np.log(Y)
    
    print(X)
    print(Y)
    
    # 기울기와 절편을 구한 후 그래프와 차트를 출력합니다. 
    slope, intercept = do_linear_regression(X, Y)
    draw_chart(X, Y, slope, intercept)
    
    return slope, intercept


# read_data() - words.txt에 저장된 단어와 해당 단어의 빈도수를 리스트형으로 변환합니다.
def read_data():
    # words.txt 에서 단어들를 읽어, 
    # [[단어1, 빈도수], [단어2, 빈도수] ... ]형으로 변환해 리턴합니다.
    words = []

    filename = 'words.txt'

    x = []
    y = []

    with open(filename) as data:
        lines = data.readlines()
        
    for line in lines:
        word = line.replace('\n','').split(',')
        word[1] = int(word[1])
        words.append(word)
    return words

# do_linear_regression() - 임포트한 sklearn 패키지의 함수를 이용해 그래프의 기울기와 절편을 구합니다.
def do_linear_regression(X, Y):
    # do_linear_regression() 함수를 작성하세요. 
    X = X.reshape(-1,1)
    li = LinearRegression()
    li.fit(X,Y)
    
    slope = li.coef_[0] # 2번째 변수에 대한 계수 (신문)
    intercept = li.intercept_ #
    

    return (slope, intercept)


# draw_chart() - matplotlib을 이용해 차트를 설정합니다.
def draw_chart(X, Y, slope, intercept):
    fig = plt.figure()
    ax = fig.add_subplot(111)
    plt.scatter(X, Y)

    # 차트의 X, Y축 범위와 그래프를 설정합니다.
    min_X = min(X)
    max_X = max(X)
    min_Y = min_X * slope + intercept
    max_Y = max_X * slope + intercept
    plt.plot([min_X, max_X], [min_Y, max_Y], 
             color='red',
             linestyle='--',
             linewidth=3.0)
    
    # 기울과와 절편을 이용해 그래프를 차트에 입력합니다.
    ax.text(min_X, min_Y + 0.1, r'$y = %.2lfx + %.2lf$' % (slope, intercept), fontsize=15)
    
    plt.savefig('chart.png')
    elice_utils.send_image('chart.png')

if __name__ == "__main__":
    main()