[Algorithm] LIS(Longest Increasing Subsequence) 최장 증가 부분 수열 알고리즘

LIS 란

let 'A' is Array
assume that A consists of natural numbers.
A = [2,7,1,6,4,9]

위의 조건에 A에 LIS 를 구하라고 말을 한다면,
[2,7,1,6,4,9] 가 선택되어 [2,4,9]가 최장 증가 부분 수열이 된다.
즉, 수열 내에서 숫자가 증가되는 부분 수열들 중에 가장 긴 부분 수열을 뽑으면 된다.

✍️접근 방식

• Brute Force
  시간 복잡도 : O(2ⁿ)
• dp
  시간 복잡도 : O(N²)
• 이분 탐색
  시간 복잡도 : O(Nlog₂N)

먼저, Brute Force를 통한 접근을 하게 되면, 수열내에 존재하는 모든 부분 수열을 구해야한다.

dp를 통한 접근은, 메모이제이션 기법을 활용해서 해결할 수 있다.

• 변수 i가 n 까지의 반복
  • 변수 j가 i 까지의 반복
    • arr[j] < arr[i] 의 조건이면 현재 이전의 data보다 현재의 data가 크기 때문에 최장 부분 수열이 된다. dp[i] = dp[j] + 1로 갱신을 해주게 된다.

위의 방식은 메모이제이션을 사용하긴했지만, N²이라는 아직까지 높은 시간복잡도를 띄게 된다.

마지막으로, 이분탐색을 통한 접근은 매우 간단하고, 속도 또한 가장 빠르다. 아래의 cpp로 구성된 코드를 보면서 이해하는 것이 가장 빠를 것 같다.

#include <iostream>
#include <algorithm>

int main(){
	int arr[6] = {2,7,1,6,4,9};
    int lis[6];
    int k = 0;
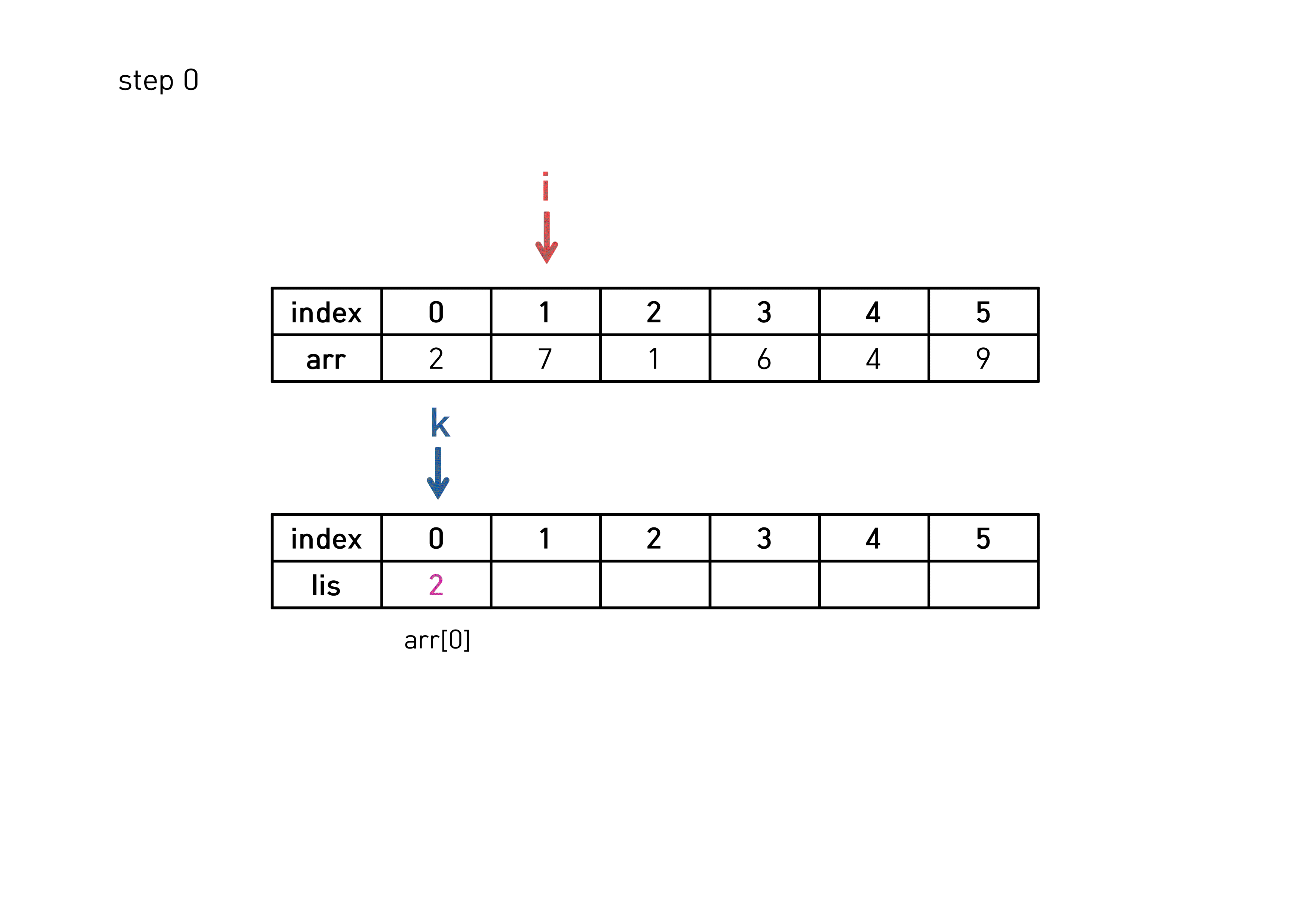
    lis[k] = arr[k];
    
    for(int i=1;i<6;i++){
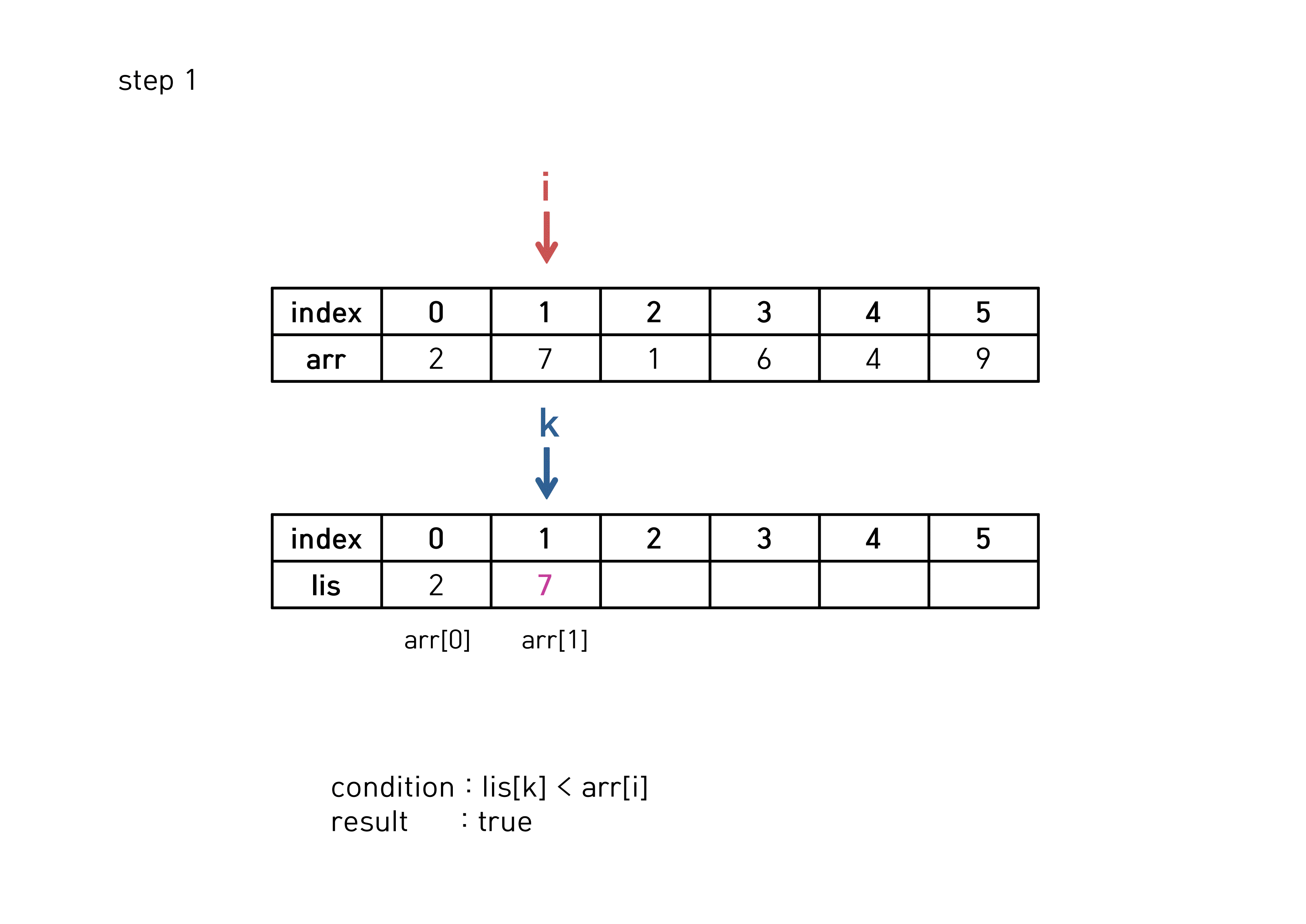
    	if(lis[k] < arr[i]){ //dp때와 마찬가지로, 증가하는 부분수열 조건
        	lis[++k] = arr[i];
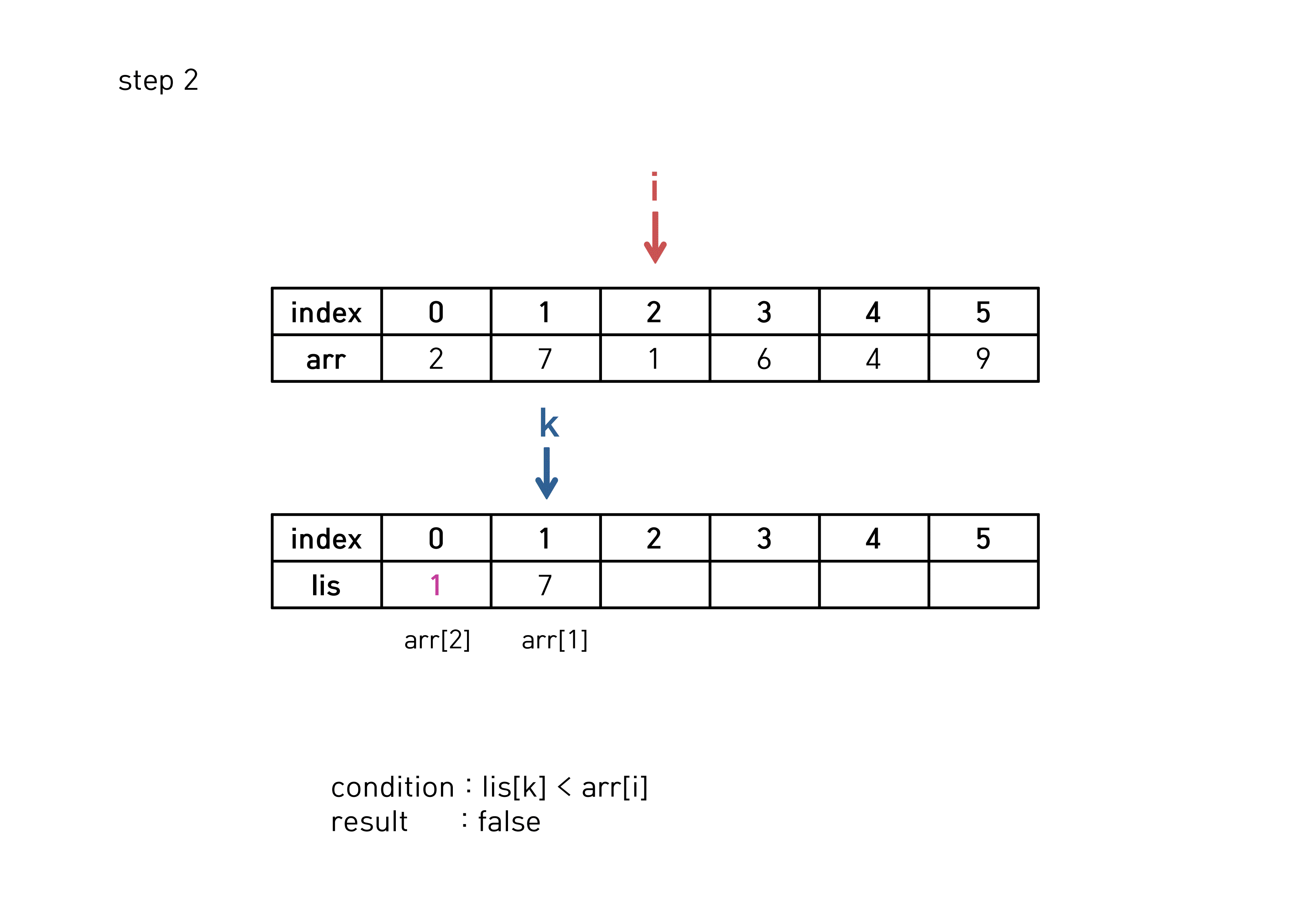
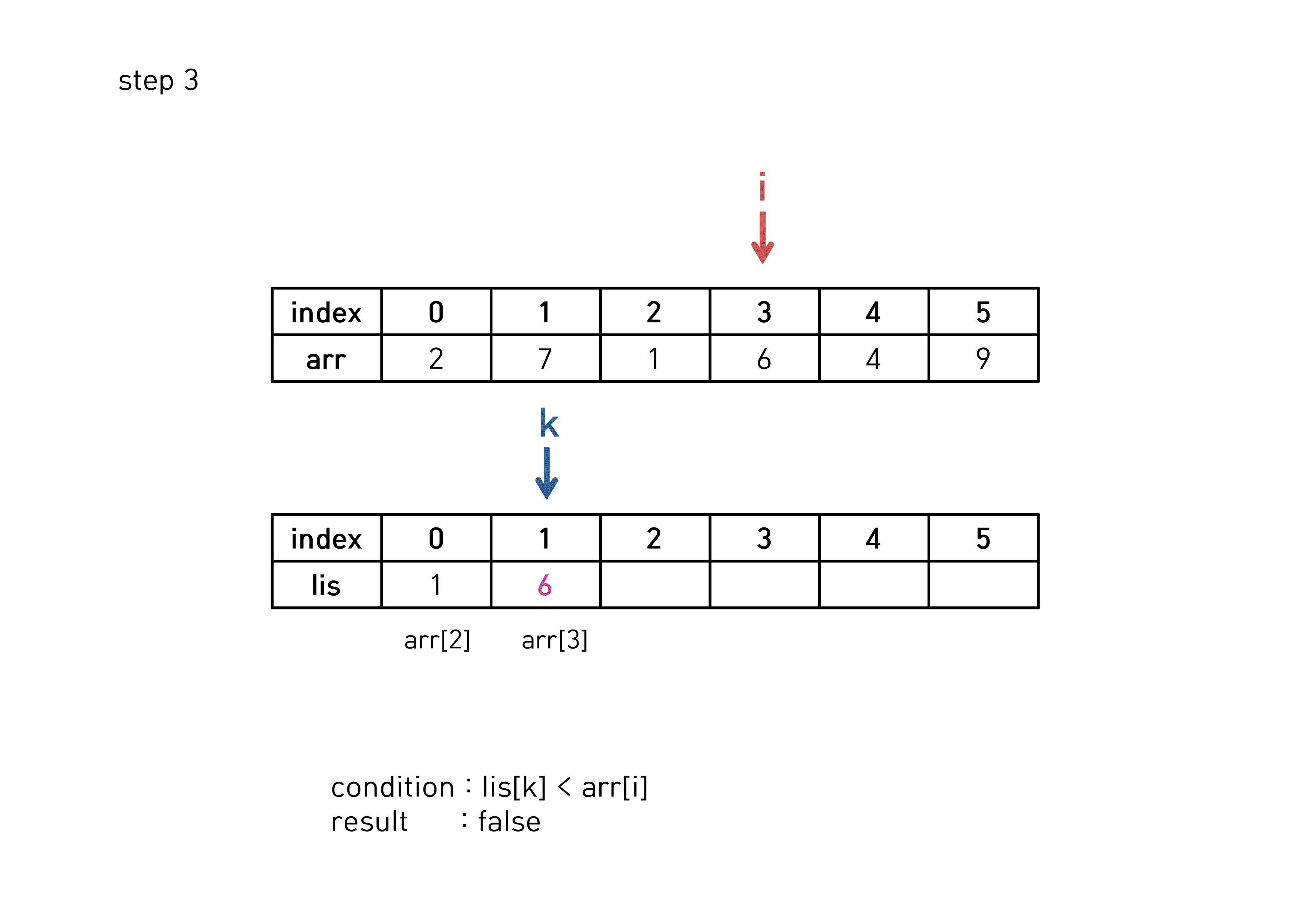
        }else{ // 증가하는 부분 수열이 아닐 때
        /**
        이전의 lis 배열 내에서 arr[i]의 lower_bound 위치를 이분탐색으로 찾는다.
       	
        찾게 되면, 해당 위치를 arr[i] 로 변경한다. 
        
        이 것은, 이론적인 이해로 보면 힘들 수도 있다.
        공부한 입장에서는 하나의 arr내에서 모든 최장 수열의 경우를 보는 것이라 생각되고,
        최장 수열이 아닐 때는 조건에서는 이전의 lis배열의 값들에 흡수 된다는 것이 맞는 것 같다.
        
        **/
        	auto lis_pointer = lower_bound(lis, lis + k + 1, arr[i]);
            (*lis_pointer) = arr[i];
		}
	}
    cout << k + 1;
}

👓시각적으로 돌아보기

LIS 알고리즘

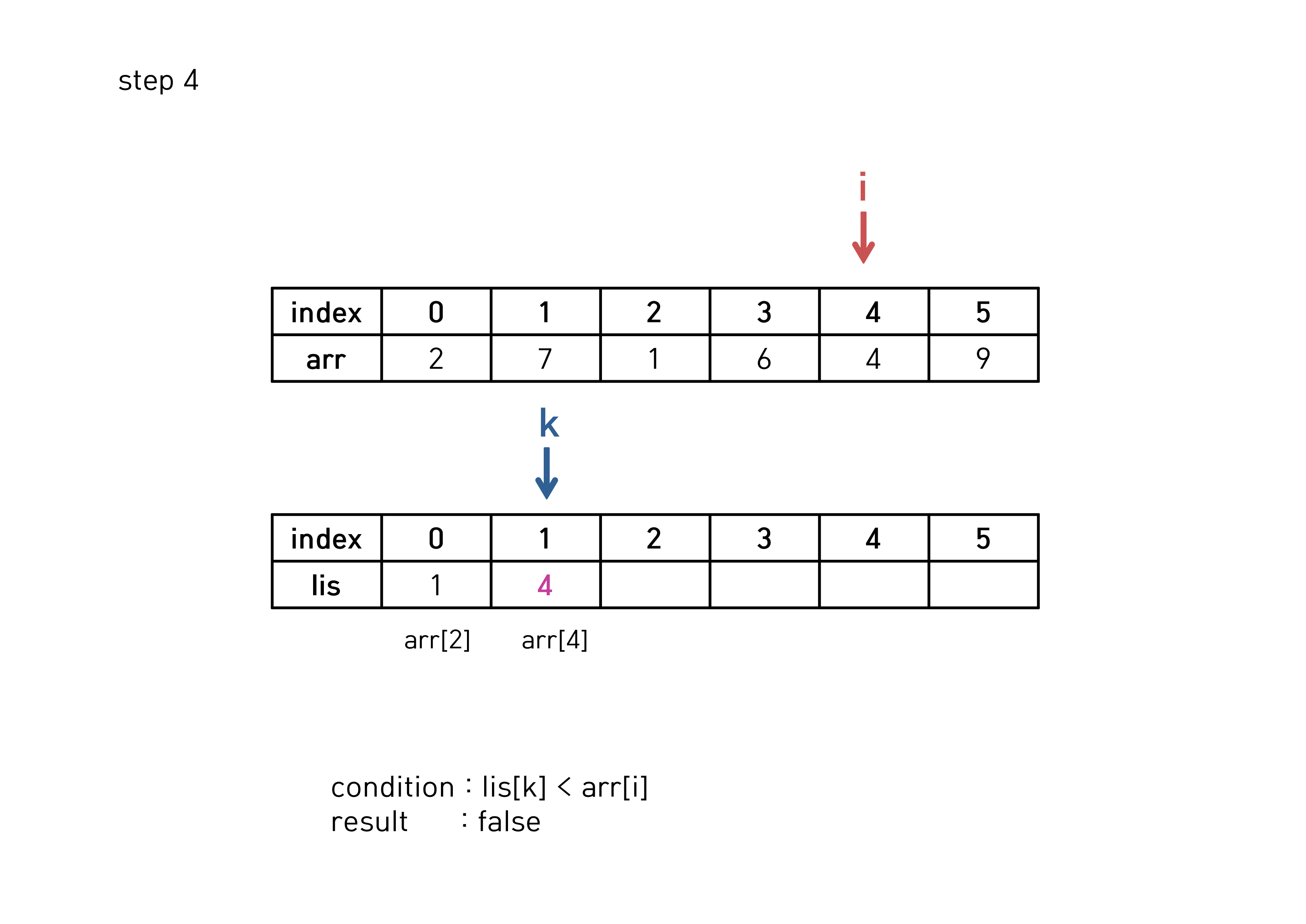
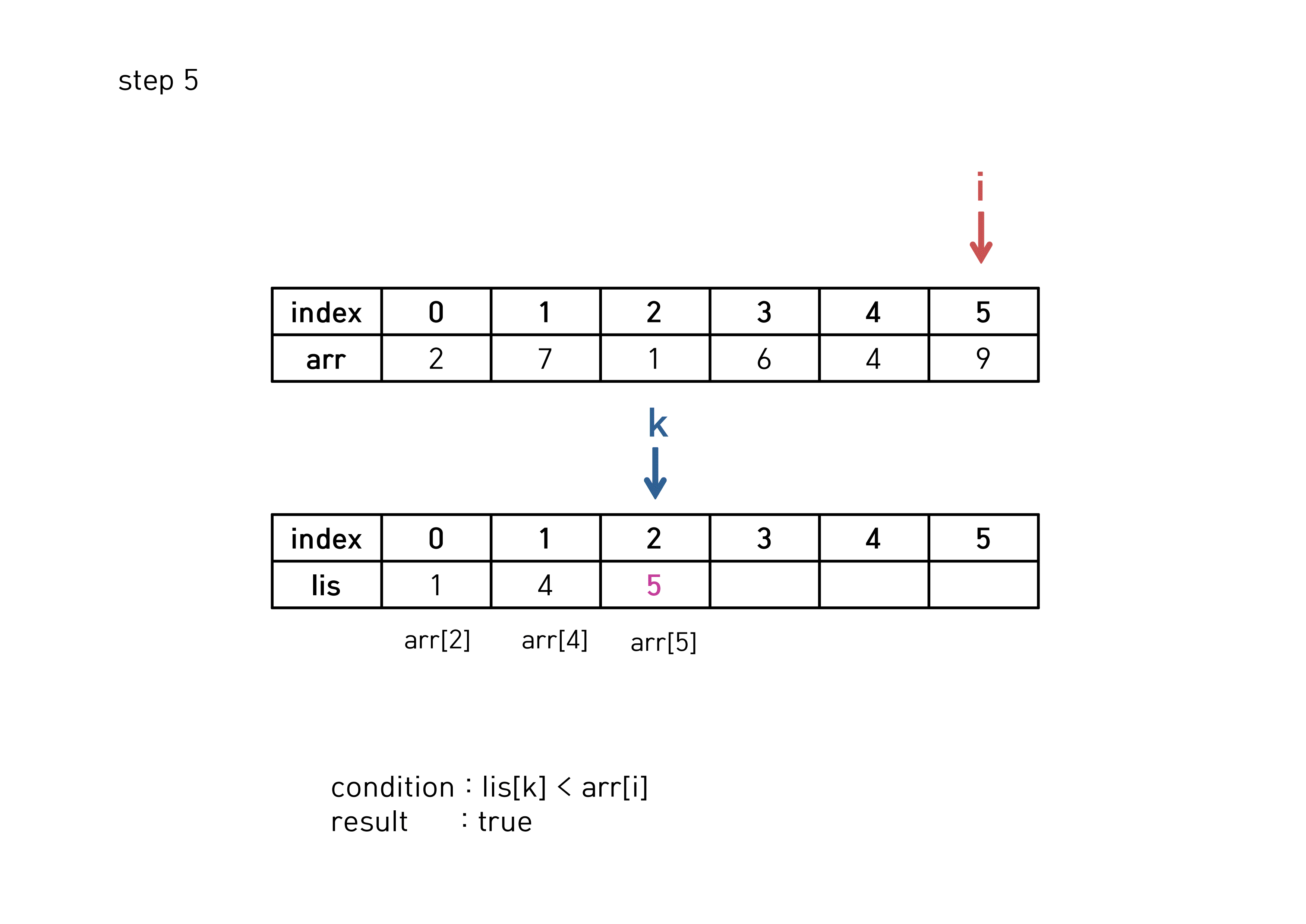
결론적으로, 길이는 k+1인 3이 LIS 의 길이가 된다.