두 변수의 관계는 매우 다양하다. 일관되게 증가할 때 증가(감소)하고 감소할 때 감소(증가)하기도 하고, 그 증가하는 비율이 동일한 경우도 있다. 이러한 관계를 상관관계라고 한다. 상관관계는 산점도를 통해 파악할 수도 있지만 데이터의 특성에 따라 계량화된 숫자로 파악하기도 한다.
상관성을 계량화하면 정도를 명확히 파악하거나 비교를 하는데 유리한 점도 있지만, 무엇보다도 표본을 통해 실제로 모집단에서 변수간 상관성이 존재하는지 가설검정할 수 있다는 데 커다란 장점이 있다.
본 글에서는 상관관계를 계산하는 지표 중 모수적 방법인 Pearson상관계수와 비모수적 방법인 Spearman상관계수, Kendall의 Tau를 자세히 알아보고자 한다.
-
Pearson 상관계수
-
개념
정규분포를 따르면서 등간척도 및 비율척도로 측정된 두 변수의 선형 상관관계를 측정하는 방식이다. -
특징
선형이라는 의미가 중요한데, 곡선 등 비선형 상관관계가 있는 경우 Pearson상관계수는 낮게 나온다.변수 간 선형관계를 파악하므로 이상치에 민감하다.
-
산출방식
두 변수의 공분산에 변수별 표준편차의 곱을 나누어 구한다. 구체적인 공식은 아래와 같다.
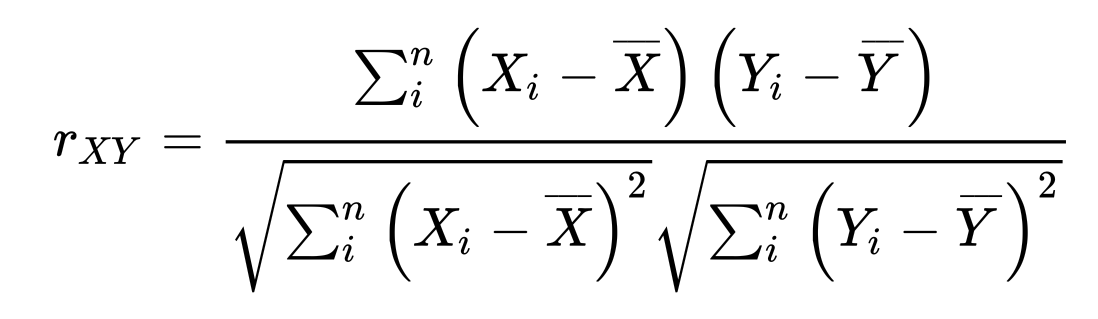
여기서 분자는 공분산(Covariance), 분모는 개별 변수의 표준편차의 곱으로 볼 수 있다.(1/(n-1)항은 분모분자에서 소거)
공분산은 (1) 두 변수 간 변동의 방향이 동일하고 (2) 두 변수의 변동 폭이 동일할 때 가장 커지는데, 두 조건을 충족하는 관계는 선형관계이다.
이러한 특징을 통해 Pearson 상관계수가 두 변수의 선형관계를 단위 표준화한 것이라는 점을 알 수 있다.
-
가설검정
피어슨 상관계수는 아래와 같이 변형하면 자유도가 n-2인 t분포를 따르는 것으로 알려져있으며 양측검정 기준으로 p-value를 계산하여 검정한다.
-
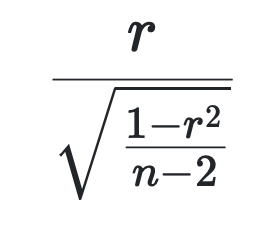
파이썬 코드
scipy.stats 라이브러리에서 pearsonr 메소드를 이용해 상관계수와 p-value를 간편하게 구할 수 있다. 수기로 계산하는 과정은 아래와 같다.
def pearson(x, y): mean_x = np.mean(x) mean_y = np.mean(y) dev_x = x - mean_x dev_y = y - mean_y nom = np.dot(dev_x, dev_y) denom = (sum(dev_x**2) * sum(dev_y**2)) ** 0.5 corr_coef = nom/denom from scipy.stats import t n = len(x) T = r*((n-2)/(1-r**2))**0.5 rv = t(df = n-2) p_value = (1 - rv.cdf(T))*2 return corr_coef, p_value
-
-
Spearman 상관계수
-
개념
pearson상관계수와 달리 데이터의 척도가 서열 척도인 경우 사용한다. 값 자체의 의미보다 크기의 순서가 중요하기 때문에 pearson 상관계수에 순위를 적용해서 산출한다.
-
특징
선형 상관관계가 아닌 두 변수 간 단조관계를 파악한다.
순위 자료를 이용하므로 이상치에 덜 민감하다. -
산출방식
피어슨 상관계수 공식과 동일하나, 관측값이 아닌 관측값의 순위를 대입해서 산출한다.
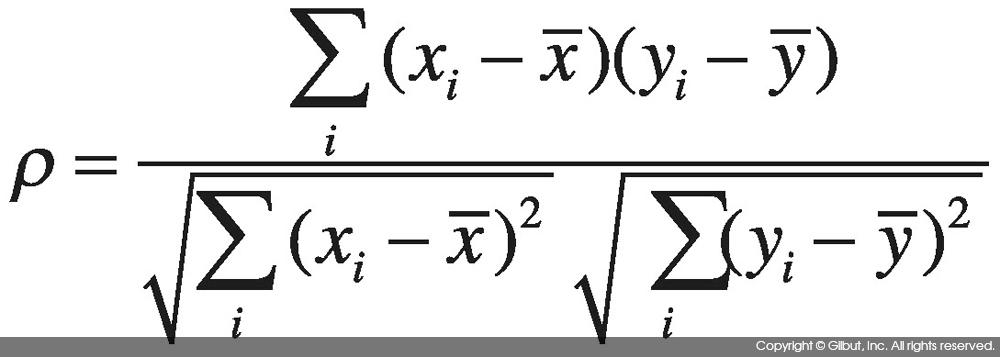출처: The Book -
가설검정
스피어만 순위상관계수 검정은 비모수 검정으로, 모분포에 대한 가정 없이 사전에 구해진 누적확률분포표를 이용해서 가설검정한다. 다만, 스피어만 순위상관계수를 표준화시키면 대표본 근사 시 아래와 같이 점근적으로 표준정규분포를 따르는 것이 알려져있다.
-
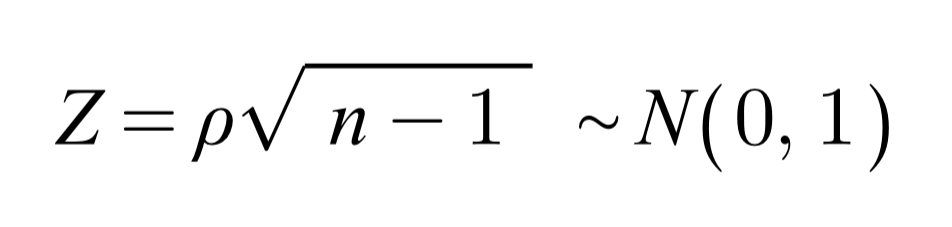
파이썬 코드
scipy.stats 라이브러리에서 spearmanr 메소드를 이용해 상관계수와 p-value를 간편하게 구할 수 있다. 수기로 계산하는 과정은 아래와 같다.
spearmanr 메소드를 이용해 p-value를 계산하면 순위데이터에 pearson 상관계수의 p-value를 계산한 것과 같은 값이 나오는데 위 통계량을 이용해 표준정규분포를 이용해 계산한 결과보다 조금 작다.
def spearman(x, y): mean_x = np.mean(x) mean_y = np.mean(y) dev_x = x - mean_x dev_y = y - mean_y nom = np.dot(dev_x, dev_y) denom = (sum(dev_x**2) * sum(dev_y**2)) ** 0.5 r = nom/denom from scipy.stats import norm n = len(x) var0 = 1/(n-1) rv = norm(0, 1) Z = r*(n-1)**0.5 p_value = (1 - rv.cdf(Z))*2 return r, p_value
-
-
Kendall의 Tau
-
개념
spearman의 순위상관계수와 유사하게 서열척도를 대상으로 상관계수를 구하는 방법이다.
-
특징
spearman상관계수와 달리 순서가 아닌 부합성을 이용해서 상관계수를 구한다. 즉, 변수별 두 관측치 간 차이의 부호가 같으면 점수를 부여하고 모든 관측치간 조합의 수에서 부호가 같은 조합의 비율을 구한다.
-
산출방식
: 관측값 쌍의 한 변수에서 값이 증가할 때 다른 한 변수의 값도 증가하는 경우의 수
: 관측값 쌍의 한 변수에서 값이 증가할 때 다른 한 변수의 값은 감소하는 경우의 수
, : 첫 번째 변수와 두 번째 변수에서 동일한 값이 있는 관측값의 수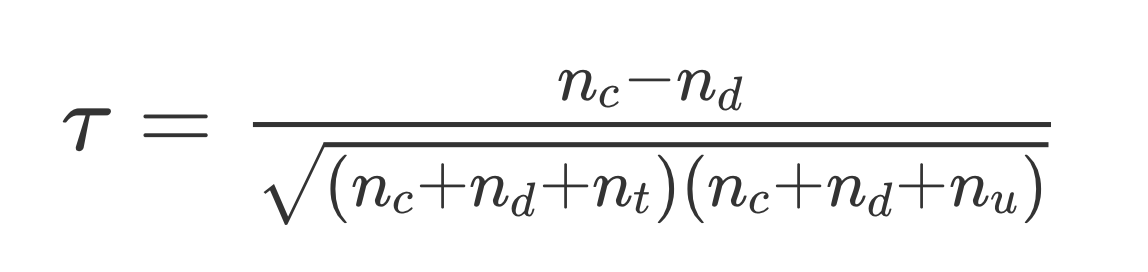
-
가설검정
켄달의 타우 검정은 비모수 검정으로, 모분포에 대한 가정 없이 사전에 구해진 누적확률분포표를 이용해서 가설검정한다. 켄달의 타우를 표준화시키면 대표본 근사 시 점근적으로 표준정규분포를 따르는 것이 알려져있다.
-
파이썬 코드
scipy.stats 라이브러리에서 kendall 메소드를 이용해 상관계수와 p-value를 간편하게 구할 수 있다. 수기로 계산하는 과정은 아래와 같다.
P, Q, T, U = 0, 0, 0, 0 for i in range(len(df) - 1): for j in range(i+1, len(df)): if (df.score[i] - df.score[j]) * (df.preference[i] - df.preference[j]) > 0: P += 1 elif (df.score[i] - df.score[j]) * (df.preference[i] - df.preference[j]) < 0: Q += 1 elif (df.score[i] - df.score[j]) == 0 and (df.preference[i] - df.preference[j]) != 0: T += 1 elif (df.score[i] - df.score[j]) != 0 and (df.preference[i] - df.preference[j]) == 0: U += 1 import numpy as np tau = (P - Q) / np.sqrt((P + Q + T) * (P + Q + U))(P - Q) / np.sqrt((P + Q + T) * (P + Q + U))
-
