[ML] 주요 머신러닝 알고리즘 - (1)

머신러닝 알고리즘은 그 종류가 워낙 많을 뿐더러 지금 이순간에도 새로운 알고리즘이 끊임 없이 개발되고 있다. 최신 기술을 습득하는 것은 일반적으로 바람직하다. 그러나 복잡한 알고리즘을 적용한 결과가 기존의 단순한 알고리즘을 적용한 결과에 비해 크게 나아지지 않는다면 우리는 단순함을 추구할 필요가 있다.

14세기 영국의 논리학자였던 William of Ockham은 중세 철학자들의 복잡하고 광범위한 논쟁을 종식시키기 위해 '오컴의 면도날'이라는 원칙을 제시하였다.

오컴의 면도날

"많은 것들을 필요없이 가정해서는 안된다"
(Pluralitas non est ponenda sine neccesitate.)
"더 적은 수의 논리로 설명이 가능한 경우, 많은 수의 논리를 세우지 말라."
(Frustra fit per plura quod potest fieri per pauciora.)

데이터분석 결과를 머신러닝을 모르는 의사결정권자에게 명확하게 전달하기 위해서는 오컴의 면도날을 적용해서 성능이 비슷하다면 최대한 간결한 모델을 사용하는 것이 바람직하지 않을까 생각한다.

그동안 머신러닝에서 기본적이지만 경험적으로 유용성이 검증된 모델을 자세히 살펴보면서 모델을 조금 더 이해하고 향후 데이터분석 결과를 전달하는 데 도움이 되고자 한다.

1. 선형 회귀(Linear Regression)

• 개념: 데이터를 가장 잘 설명하는 하나의 직선 방정식을 구함

• 방법

  • 최소제곱법(Ordinary Leat Squares): 오차의 제곱을 최소화하는 방정식을 수학적으로 계산하여 회귀계수와 절편의 추정치를 구함
  • 확률적 경사하강법(Stochastic Gradient Descent, SGD): 오차를 최소화하도록 매 랜덤샘플에서 계산된 파라미터의 값을 조금씩 조정해가면서 최적 해를 찾음

• 사용 라이브러리

  from sklearn.linear_model import LinearRegression, SGDRegressor

• 주요 파라미터(LinearRegression 기준)
  fit_intercept = True 절편을 넣을지 여부
  n_jobs = None 컴퓨팅 자원을 얼마나 쓸지 지정(-1 설정 시 모든 자원 사용)

• 주요 속성
  coef_ 추정된 회귀계수
  intercept_ 추정된 절편

2. 로지스틱 회귀(Logistic Regression)

• 개념: 종속변수가 0과 1 사이의 값을 갖는 S형의 추정식을 구함
  (모델 이름은 회귀이나 추정된 확률을 이용해 분류를 먼저 수행)

• 방법: 파라미터(절편, 회귀계수)의 함수로 이루어진 베르누이 확률분포(성공과 실패확률의 곱)를 목적함수로, 이를 최대화하는 파라미터를 추정(주로 경사하강법 또는 Newton-Raphson 방식 이용)

  📊 Newton-Raphson 방식
  함수에서 접선의 영점을 반복적으로 취해 실제 영점의 오차를 점점 줄여나가는 방식
  손실함수의 최솟값을 구할 때 사용 할 수 있으나 기울기 소실 시 수렴하지 않는 문제점 존재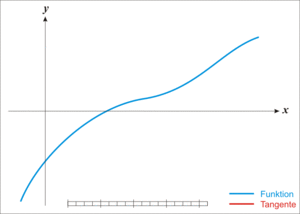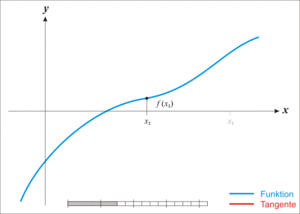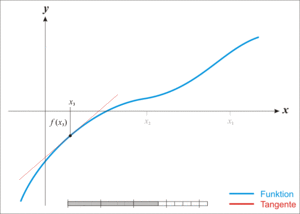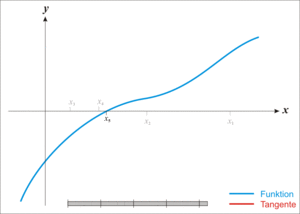Newton-Raphson 작동원리 (출처: 위키피디아)

• 사용 라이브러리

  from sklearn.linear_model import LogisticRegression
  

• 주요 파라미터
  penalty='l2' 정규항(Regularization) 타입 설정, 즉 변수가 많아질 때 목적함수에 페널티를 적용하여 과적합을 방지하는 기능 (로지스틱 머신러닝 알고리즘에 과적합 방지기능이 있다는 점이 놀랍다.)
  C 정규항의 강도, 양수이며 작을수록 강도가 세다 (과적합 방지기능이 이중으로 존재하는 셈)

3. K-최근접 이웃(K-Nearest Neighbors)

• 개념:유사한 특성을 가진 데이터는 유사한 범주에 속하는 경향이 있다는 가정으로 데이터를 분류/회귀하는 머신러닝 기법

• 방법: 학습데이터를 그대로 저장한 후 새로운 데이터 포인트에 대해 학습데이터에서 가장 가까운 k개의 데이터 포인트를 찾아 그것들로부터 새로운 데이터 포인트의 범주를 라벨링

• 사용 라이브러리

  from sklearn.neighbors import KNeighborsClassifier, KNeighborsRegressor
  

• 주요 파라미터
  n_neighbors=5 분류 또는 회귀에 사용할 주변 데이터포인트의 수
  weights='uniform' 거리 가중치, 'distance'로 지정하면 가까운 데이터포인트가 많은 영향을 미침

• 주요 속성
  classes_ 모델이 학습한 분류 종류

4. 나이브 베이즈(Naive Bayes)

• 개념: 베이즈 정리를 적용한 조건부 확률 기반의 분류 모델이며

• 방법: 정답(Y)과 정답의 특성(X)을 학습하고 특성만 발견되는 경우 정답일 확률을 구함

  베이즈정리
  두 확률변수의 사전확률과 사후확률 사이의 관계를 나타내는 정리
  스팸메일인 사건을 $A_1$
  정상메일인 사건을 $A_2$
  스팸메일에 등장하는 어휘의 사건집합을 $B$라고 한다면

  ▼ 스팸 예측 <<<<<<<<<<<<<<<<<<<<<<<<<<<<<<<< ▼ 데이터 학습

  $P(A_1|B) = \frac{P(B \cap A_1)}{P(B)} = \frac{P(B|A_1)P(A_1)}{P(B)} = \frac{P(B|A_1)P(A_1)}{P(B|A_1)P(A_1) + P(B|A_2)P(A_2)}$

• 사용 라이브러리

  from sklearn.naive_bayes import GaussianNB
  

• 주요 파라미터
  priors=None 클래스의 사전 확률 $P(A_1)$

• 주요 속성
  class_prior_ 클래스의 발생확률
  classes_ 분류기에 입력된 클래스의 라벨

5. 의사결정나무(Decision Tree)

• 개념: 의사결정규칙을 나무 구조로 나타내어 전체 자료를 몇 개의 소집단으로 분류하거나 예측을 수행하는 분석방법
  (트리 기반 알고리즘의 기초가 되는 알고리즘이기 때문에 단순한 알고리즘이나 매우 중요하다!)

• 방법: 지니지수를 감소시키거나 엔트로피지수가 가장 작은 최적 분리에 의해 자식마디를 형성

  불순도 측도
  동질적인 자료가 많으면 불순도가 낮고 이질적인 자료가 많으면 불순도가 높은 것으로 본다.

  ① 카이제곱 통계량: $\chi^2 = \sum_{i=1}^{n} \frac{(O_i - E_i)^2}{E_i}$

  ② 지니지수: $Gini = 1 - \sum_{i=1}^{n} \left(\frac{x_i}{\sum_{i=1}^{n} x_i}\right)^2$

  ③ 엔트로피: $H(X) = -\sum_{i=1}^{n} p(x_i) \log_2p(x_i)$

• 사용 라이브러리

  from sklearn.tree import DecisionTreeClassifier, DecisionTreeRegressor
  

• 주요 파라미터

  criterion='gini' 분기의 품질을 측정하는 함수, {"gini", "entropy", "log_loss"} 중 선택 가능
  splitter='best' 매 노드의 분기 전략이며 'best'는 모든 변수에 대해 최적 분기, 'random'은 임의로 고른 변수에 대해 최적 분기 진행
  max_depth=None 트리의 최대 깊이, 따로 지정하지 않으면 불순도가 0이 될 때까지 분기
  min_samples_split=2내부노드를 분할하는 데 필요한 최소 샘플 수를 설정
  min_samples_leaf=1 리프노드에 있어야 하는 최소 샘플 수를 설정
  max_features=None 최적 분기를 찾을 때 고려하는 변수의 갯수 설정, 수치로 입력할 수도 있고 적용함수를 {"sqrt", "log2"}로 설정할 수도 있음
  random_state=None 분기에 이용할 변수 선택 시 임의 상태를 설정
  max_leaf_nodes=None결정트리의 최대 리프노드 갯수
  ccp_alpha=0.0 모델 복잡도 및 과적합 완화를 위해 가지치기의 정도를 결정

• 주요 속성
  feature_importances_ 변수 중요도를 반환하며 값이 클수록 중요한 변수, 해당 변수로 인해 감소하는 불순도의 정도로 계산

• (참고) 의사결정나무 시각화

  분기점과 샘플 수, 리프노드의 불순도를 시각화한다. (아래 코드 예시)

  from sklearn import tree
  tree.plot_tree(dt_model,
                feature_names = ['x1','x2'],
               class_names = ['0','1'], filled = True)
  plt.tight_layout()
  plt.show()

6. 랜덤포레스트(Random Forest)

• 개념: 앙상블 배깅 모델의 일종으로, 랜덤으로 생성된 무수히 많은 트리를 이용하여 예측하는 알고리즘

• 방법: 무수히 많은 의사결정나무 모델을 적합하여 각 모델의 예측 결과를 결합(분류는 투표/회귀는 평균), 개별 의사결정나무 모델링 시 붓스트랩 샘플을 이용하여 데이터의 무작위성을 추가로 부여

  배깅(Bagging, Bootstarp Aggregating)과 붓스트랩(Bootstrap)

  붓스트랩이란 주어진 자료에서 단순랜덤 복원추출 방법을 활용하여 동일한 크기의 표본을 여러 개 생성하는 샘플링 방법을 의미하며, 배깅은 이러한 붓스트랩 샘플을 이용한 앙상블모델을 의미

• 사용 라이브러리

  from sklearn.ensemble import RandomForestClassifier, RandomForestRegressor
  

• 주요 파라미터

  의사결정나무 주요 파라미터+
n_estimators=100 사용할 의사결정나무 모델의 수
  max_features='sqrt' 의사결정나무 모델과 동일하나, 변수 갯수의 제곱근만큼만 사용
  bootstrap=True 트리를 만들 때 붓스트랩 샘플을 이용할지 여부 설정, False 설정 시 전체 데이터세트를 사용
  oob_score=False out-of-bag 샘플을 이용하여 모델의 정확도를 측정할지 설정, (bootstrap=False 설정 시 사용 불가)

  Out-Of-Bag 샘플

  붓스트랩 샘플링에서 추출되지 않은 나머지 데이터샘플
  즉, 붓스트랩 샘플링은 전체 데이터를 'in-the-bag' 샘플과 'out-of-bag' 샘플로 나눠 복원추출한다.

• 주요 속성

  의사결정나무 주요 속성+
oob_score_ out-of-bag 샘플을 이용해 측정한 모델의 정확도

7. XGBoost

• 개념: 앙상블 부스팅 모델의 일종으로, 순차적으로 의사결정나무 모델을 만들어 이전 모델로부터 더 나은 모델을 만들어내는 알고리즘

• 방법: 이전 의사결정나무모형에서 예측이 잘못된 데이터에 가중치를 반영해서 다음 모형으로 모델링하는 작업을 반복하면서 예측 오차를 줄여나감

  • 데이터 과적합 방지를 위한 정규화 기법을 내장하여 예측의 안정성 확보

• 사용 라이브러리

  from xgboost import XGBClassifier, XGBRegressor
  

• 주요 파라미터

  의사결정나무 주요 파라미터+
booster='gbtree' 사용할 부스팅 모델의 종류, {gbtree, gblinear, dart}
  grow_policy 'depthwise' 루트 노드에 가장 가까운 노드에서 분할, 'lossguide' 손실 변화가 가장 큰 노드에서 분할
  learning_rate=0.3 부스팅 learning rate, 값이 크면 발산할 가능성이 있으며 값이 작으면 처리 속도가 느린 단점이 있음
  gamma=0 분기를 하기 위한 최소 손실함수 감소량
  reg_alpha=0 L1(릿지) 규제의 가중치
  reg_lambda1=1 L2(라쏘) 규제의 가중치
  importance_type feature importance 타입, 분류모델인 경우 {"gain", "weight", "cover", "total_gain", "total_cover"} 중 선택, 회귀모델인 경우 'weight'만 선택

8. K-Means Clustering

• 개념: 사전에 지정한 K개의 클러스터를 기준으로 클러스터 중심과 데이터 거리 차이의 분산을 최소화하도록 군집하는 알고리즘

• 방법: 군집 수만큼 임의의 중심을 선정하고 해당 중심점과 거리가 가까운 데이터를 그룹화한 후 중심이 이동하지 않을 때까지 현행화하면서 군집을 반복

  • 군집 수를 사전에 지정해줘야하며, 이를 위해 중심과의 오차제곱합이 크게 감소하는 군집 수 또는 실루엣 계수가 높은 군집 수를 이용

• 사용 라이브러리

  from sklearn.cluster import KMeans
  

• 주요 파라미터

  n_clusters=8 사전에 지정할 군집의 갯수
  init='k-means++' 초기 군집 중심 지정 방법, 'k-means++' 설정 시 데이터 일부를 샘플링하여 지정하며, 'random' 설정 시 무작위로 초기 중심을 지정
  n_init='auto' K-Means 알고리즘을 수행할 횟수, init이 'K-means++'이면 1번, 'random'이면 10번 수행
  max_iter=300 군집의 중심이 수렴할 때까지 반복하는 횟수
  random_state=None 초기 중심 지정 시 무작위 상태
  algorithm='lloyd' 사용할 K-means 알고리즘의 종류, 'lloyd'는 전통적인 EM(Expectation-Maximization) 알고리즘, 'elkan' 알고리즘은 군집이 잘 정의되었을 때 효율적

• 주요 속성

  cluster_centers_ 군집 중심위치
  labels_ 모든 샘플데이터에 대한 군집(라벨)
  inertia_ 군집 중심으로부터 거리의 제곱합, 최적 군집 수 파악 시 주로 활용