[프로젝트] 마케팅데이터 고객 클러스터링 - (3) RFM분석을 이용한 지역별 군집

군집 단위 결정

• 거래별 데이터 편중이 심한 것을 고려하여 상위 범주인 고객 또는 지역별 군집을 검토하였다.

• 설정한 가설에 따라 고객 그룹별 위치 파악을 위해 지역별 군집을 진행하였다.

군집분석 개요

• [단위변수] customer_zip_code_prefix(이하 Zipcode)
  : 우편번호 앞 4자리, 도시 내 상세 위치 파악 가능

• [활용변수] 군집에는 변수를 직접적으로 사용하기보다 마케팅의 구성요소를 잘 반영할 수 있는 RFM 변수를 생성하여 이용하였다.

  RFM이란?

  가치있는 고객을 추출해내어 이를 기준으로 고객을 분류할 수 있는 매우 간단하면서도 유용하게 사용될 수 있는 방법으로 알려져 있어 마케팅에서 가장 많이 사용되고 있는 분석방법 중 하나

  • Recency - 거래의 최근성: 고객이 얼마나 최근에 구입했는가?
    → (생성변수) Zipcode별 마지막 접속시점 대비 경과일수
  • Frequency - 거래빈도: 고객이 얼마나 빈번하게 우리 상품을 구입했나?
    → (생성변수) Zipcode별 order_id_nunique를 합산
  • Monetary - 거래규모: 고객이 구입했던 총 금액은 어느 정도인가?
    → (생성변수) Zipcode별 payment_value_sum

  [내용출처: 위키피디아]

• [알고리즘] 직관적으로 이해가 쉽고 원형 데이터에서 군집이 잘 이루어지는 K-Means Clustering 기법을 이용하였다.

RFM Feature Engineering

• 군집에 앞서 변수 분포의 균형을 맞추기 위해 변환 및 스케일링을 진행하였다.

• [변수변환] 데이터의 분포를 정규분포와 가깝게 만들기 위해 scipy의 Boxcox 메소드를 이용하여 적정 변환방법을 탐색하였다.

  Boxcox 변환 알고리즘에서 제시하는 변환은 Recency의 경우 제곱근, Frequency와 Monetary는 로그 변환이었다.

  Boxcox 변환이란?

  데이터가 정규분포와 상당히 벗어난 것으로 판단될 때 정규성을 갖도록 자료 변환를 변환하는 알고리즘이다. 변환 식은 아래와 같다.
  
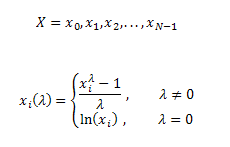
  위 공식에서 X는 주어진 값이며, 변수는 람다이다. Boxcox 메소드는 아래 가능도를 최대화하는 람다를 찾도록 알고리즘을 실행한다.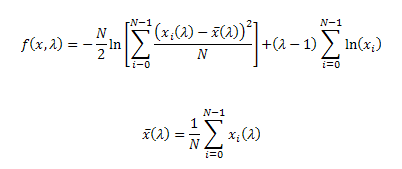

  
  [사진 출처] https://www.mql5.com/ko/articles/363

  람다에 따라 변환 방법이 달라지는데, 대략적인 구분은 아래와 같다.

• [스케일링] 변수변환 후 변수별 측정단위를 표준화하기 위해 스케일링을 진행하였다. 군집 간 특성이 명확히 드러나도록 Min-Max Scaling을 적용하였다.

• 변수변환과 스케일링을 적용한 변수별 최종 분포는 아래와 같다.
  

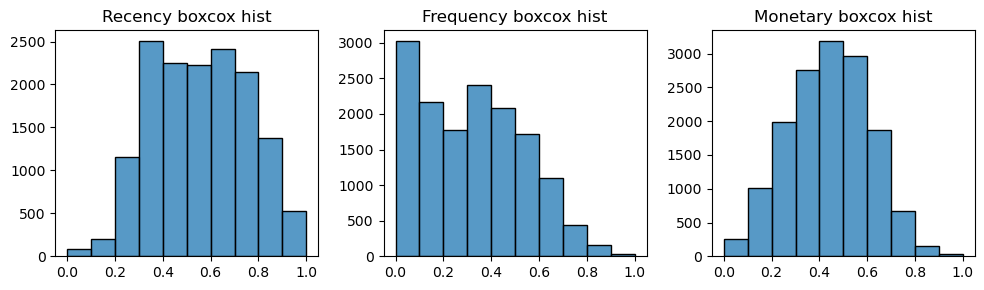
최적 군집 탐색

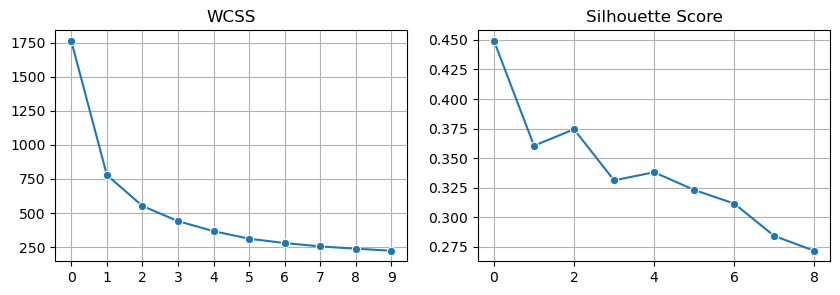
• 군집내 거리의 제곱합(Within Cluster Sum of Squares)과 실루엣 스코어를 이용해 군집 내 응집도는 높으면서 군집 간 응집도는 낮은 최적의 군집을 탐색하였다.

  분석 결과 군집 갯수가 2개일 때 실루엣 계수는 가장 높은 것으로 나타났으나 군집수에 따라 응집도가 지속적으로 증가하며 다수의 군집 간 차이 분석을 위해 군집 수를 3개로 결정하였다.
  

군집 및 시각화

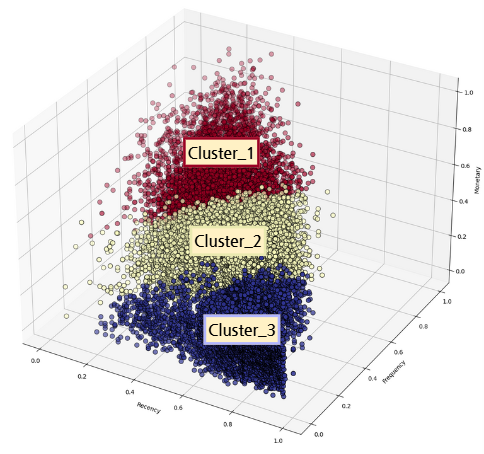
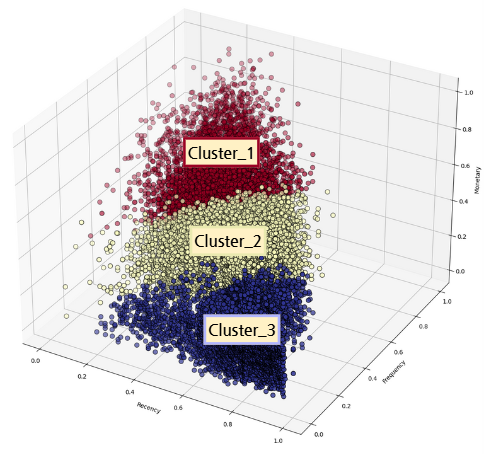
• 군집 수 3개 기준으로 군집을 수행하고 이를 시각화하면 아래와 같다.
  실루엣 스코어는 다소 낮았으나 시각적으로 세 그룹으로 군집이 잘 이루어진 것이 확인된다.
  

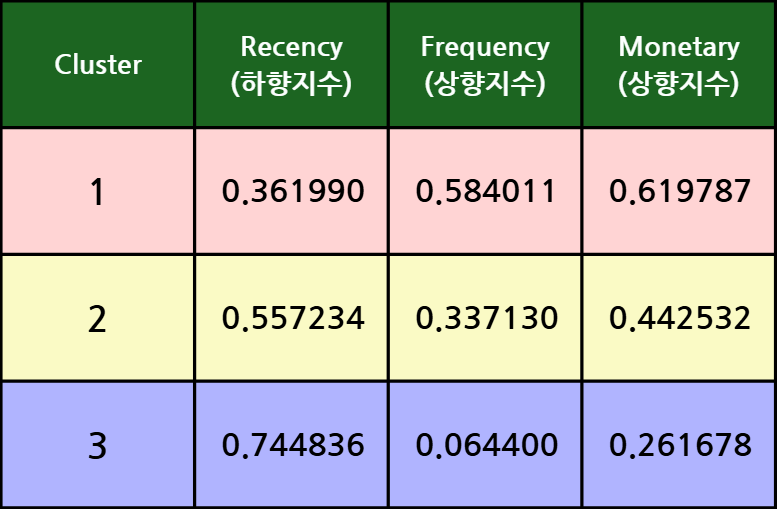
• 군집별 RFM의 평균을 살펴보면 아래와 같다.

  • 군집 1은 다른 군집에 비해 RFM이 모두 우수하였으며 (충성고객)
  • 군집 2는 보통 수준의 구매행태를 보였다. (일반고객)
  • 군집 3은 다른 군집에 비해 RFM 모두 미흡하였다. (이탈고객)
    

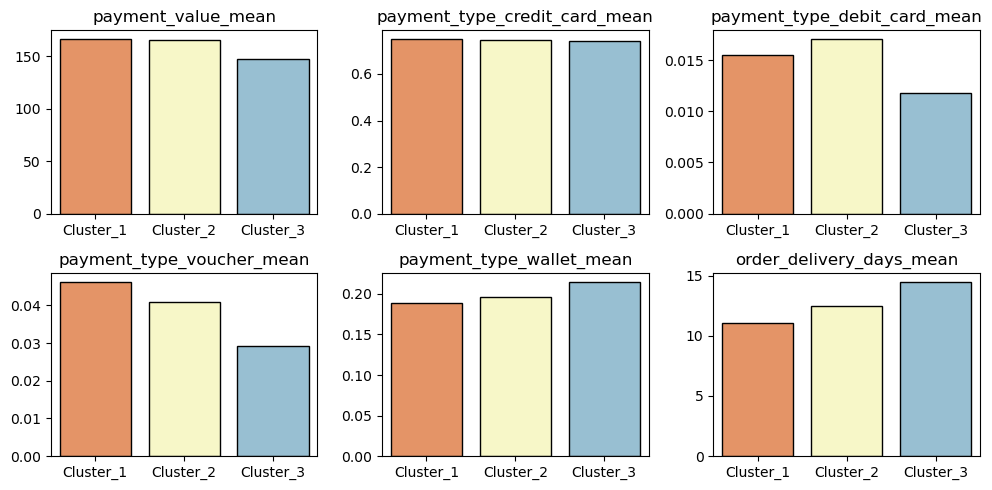
• 군집별 타 변수 평균의 차이를 보면 다음과 같다.

  • 지불 금액 및 신용카드 사용비중은 Custer_1이 높은 것으로 나타난다.
  • 직불카드, 바우처 사용비중은 Cluter_2가 높은 것으로 나타난다.
  • 지갑 사용 비중 및 배송기간은 Cluster_3이 높은 것으로 나타난다.
    특히 군집 3의 배송기간이 가장 긴 점은 해당 고객군이 이탈하게 된 주요한 원인일 가능성이 있을 것으로 판단하였다.
    

• 군집별로 구매한 상품 또한 군집별로 차이를 보였다.
  

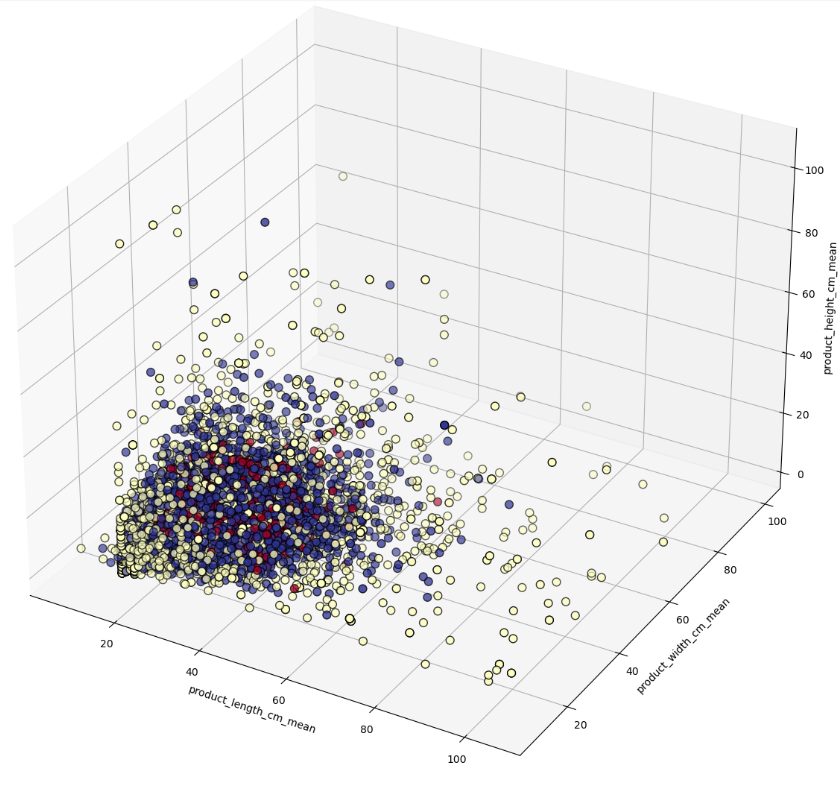
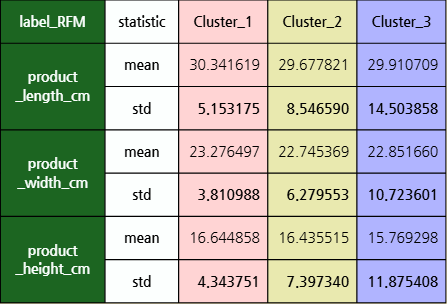
  • 상품의 평균 규격은 군집별로 큰 차이를 보이지 않았다.
  • 그러나 표준편차는 군집 3 > 군집 2 > 군집 1 순으로 달랐다.
    즉, 군집 3에 속하는 지역의 고객은 구매하는 상품의 편차가 큰 편이었다.
    

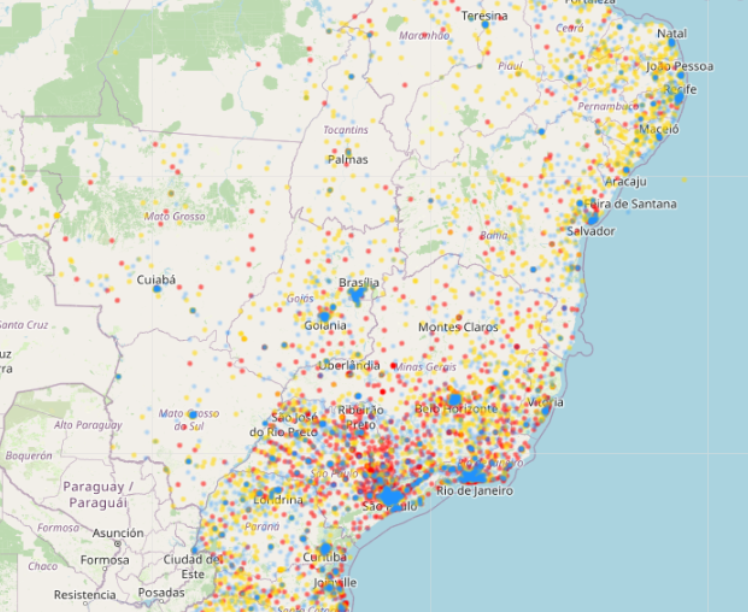
• 군집별 위치분포를 살펴보면 다음과 같다.

  • 파란색으로 표현되는 군집 3은 6시 방향의 상파울루와 리우데자네이루 등 대도시에 집중해서 분포하고 있는 것이 확인된다.
    

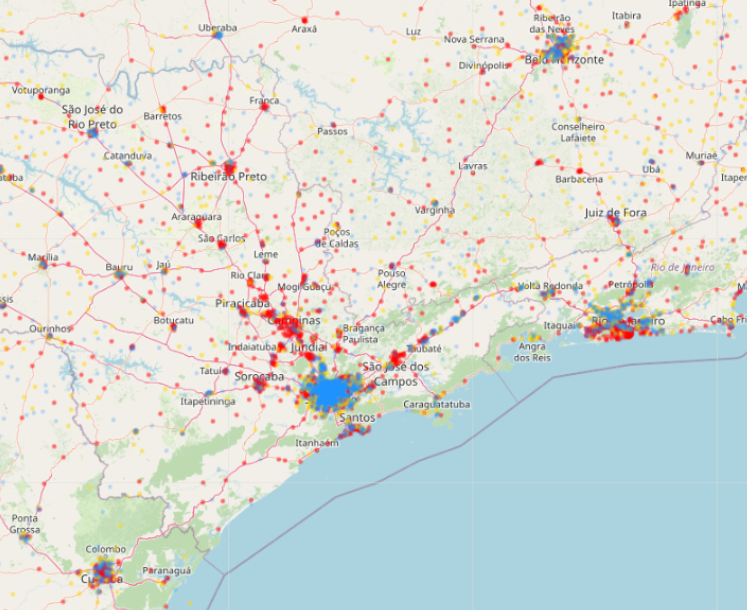
  • 상파울루와 리우데자네이루 인근으로 확대해서 살펴보면 대도시의 주변도시에 빨간색으로 표현되는 군집 1이 주로 분포하고 있는 것이 확인된다.