정렬

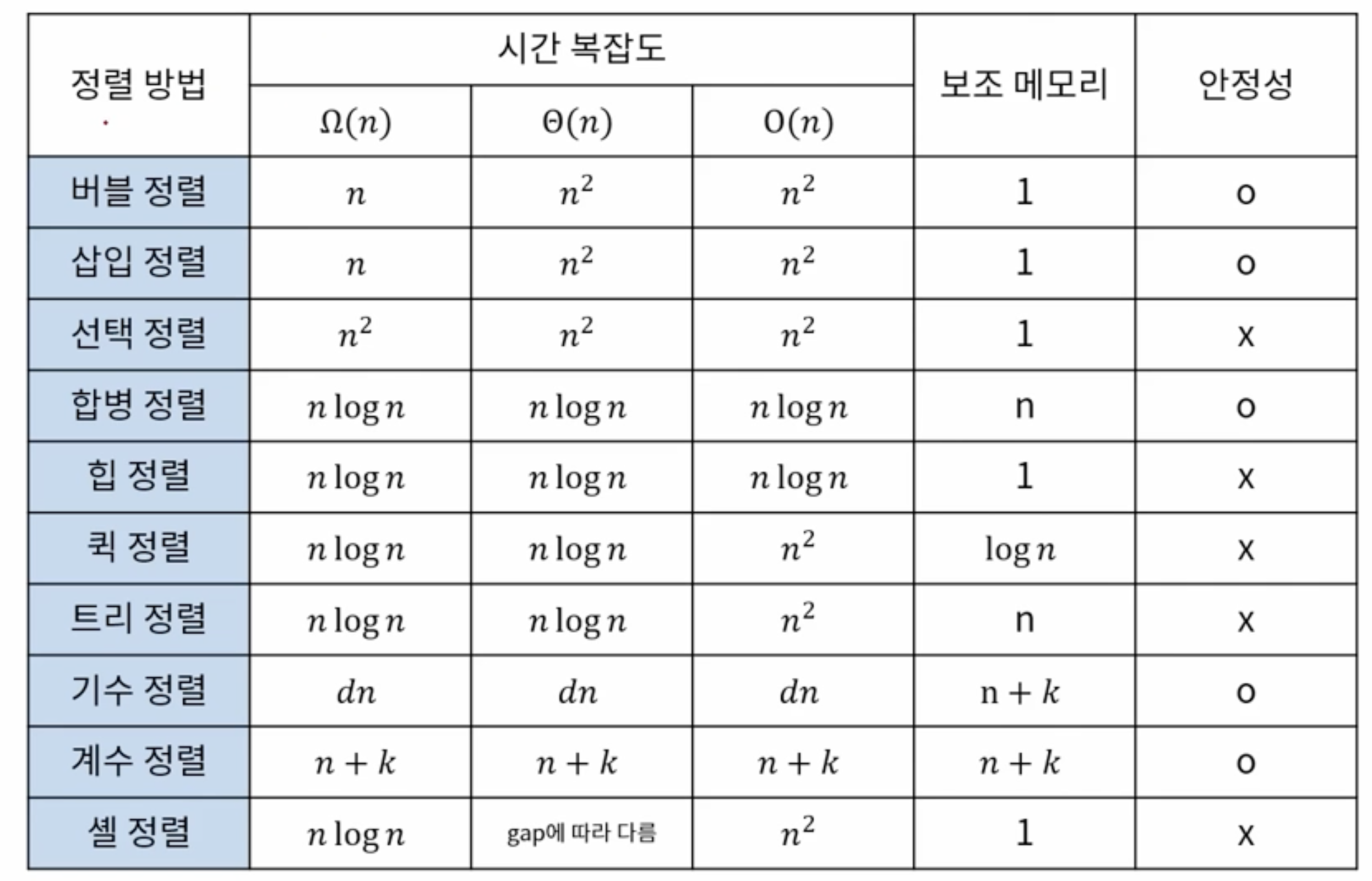
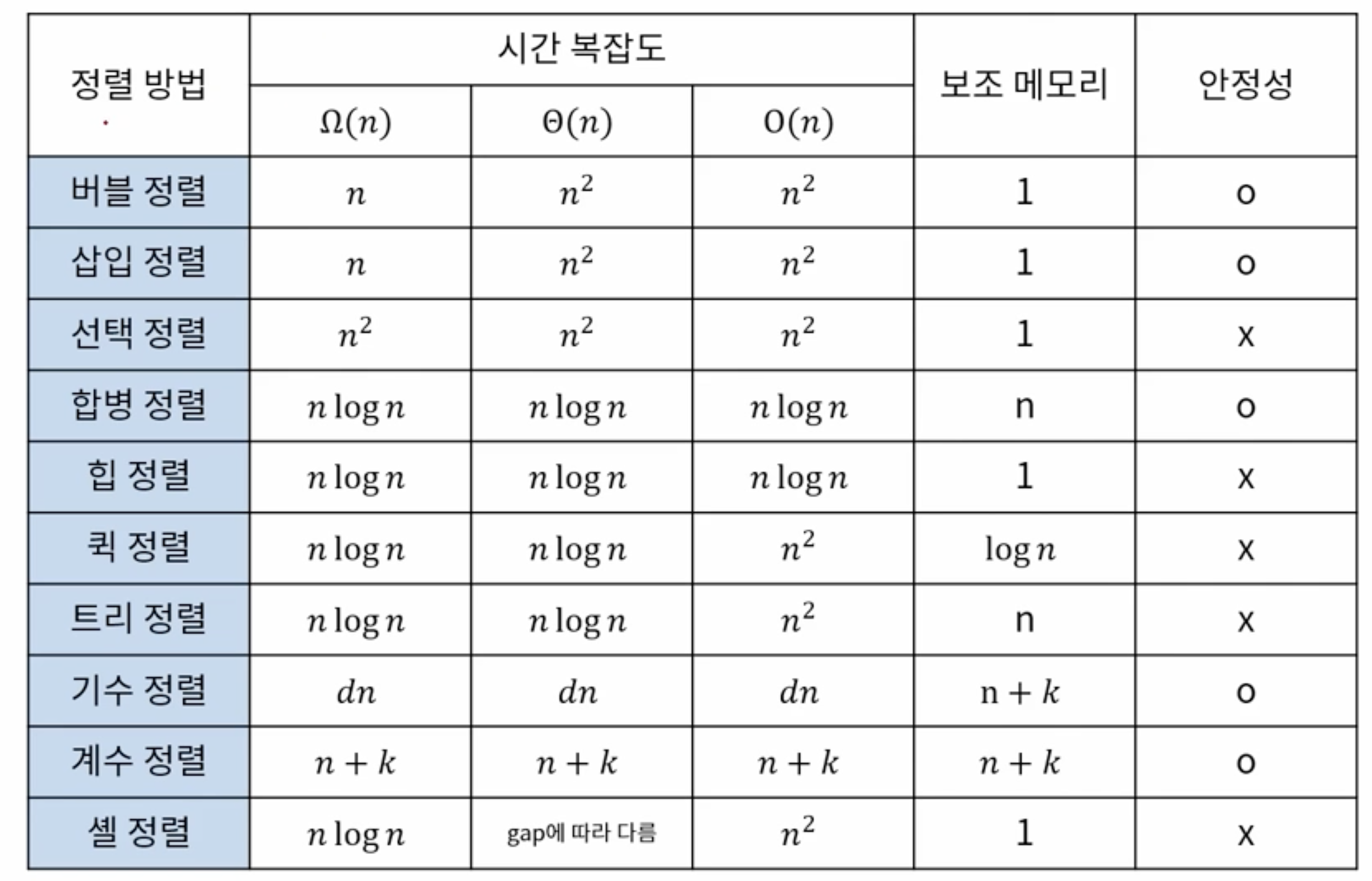
버블 정렬

• 인접한 데이터를 비교하며 자리를 바꾸는 방식
• 시간 복잡도 O(n^2)
• sudo code

bubble(arr[]){
	arr[SIZE]
    for(i=1 to SIZE-1){
    	for(j=1 to SIZE-i){
        	if(arr[j]>arr[i]){
            	swap(arr[j], arr[j+1])
            }
        }
    }
}

삽입 정렬

• 앞의 데이터를 정렬 해가면서 삽입 위치를 찾아 정렬하는 방식
• 시간 복잡도 O(n^2)
• sudo code

insert(arr[]){
	arr[SIZE]
    for(i=1 to SIZE){
    	for(j=i to 0){
        	if(arr[j]<arr[j-1]){
            	swap(arr[j], arr[j+1])
            }
        }
    }
}

선택 정렬

• 최소 또는 최대 값을 찾아서 가장 앞 또는 뒤부터 정렬하는 방식
• 시간 복잡도 O(n^2)
• sudo code

select(arr[]){
	arr[SIZE]
    for(i=0 to SIZE-1){
    	min=i
    	for(j=i+1 to SIZE){
        	if(arr[j]<arr[min]){
            	min=j
            }
        }
        swap(arr[i], arr[min])
    }
}

합병 정렬

• 배열을 계속 분할해서 길이가 1이 되도록 만들고, 인접한 부분끼리 정렬하면서 합병하는 방식
• 시간 복잡도 O(nlogn)

import java.util.Arrays;

public class MergeSort {
    public static void mergeSort(int[] arr) {
        if (arr.length <= 1) return;

        int mid = arr.length / 2;
        int[] left = Arrays.copyOfRange(arr, 0, mid);
        int[] right = Arrays.copyOfRange(arr, mid, arr.length);

        mergeSort(left);
        mergeSort(right);

        merge(arr, left, right);
    }

    private static void merge(int[] arr, int[] left, int[] right) {
        int i = 0, j = 0, k = 0;
        while (i < left.length && j < right.length) {
            if (left[i] <= right[j]) {
                arr[k++] = left[i++];
            } else {
                arr[k++] = right[j++];
            }
        }

        while (i < left.length) arr[k++] = left[i++];
        while (j < right.length) arr[k++] = right[j++];
    }

    public static void main(String[] args) {
        int[] arr = {38, 27, 43, 3, 9, 82, 10};
        mergeSort(arr);
        System.out.println("Merge Sort 결과: " + Arrays.toString(arr));
    }
}

힙 정렬

• 힙 자료구조 형태의 정렬 방식
• 기존 배열을 최대 힙으로 구조 변경 후 정렬 진행
• 시간 복잡도 O(nlogn)

import java.util.Arrays;

public class HeapSort {
    public static void heapSort(int[] arr) {
        int n = arr.length;

        for (int i = n / 2 - 1; i >= 0; i--) {
            heapify(arr, n, i);
        }

        for (int i = n - 1; i > 0; i--) {
            int temp = arr[0];
            arr[0] = arr[i];
            arr[i] = temp;

            heapify(arr, i, 0);
        }
    }

    private static void heapify(int[] arr, int n, int i) {
        int largest = i;
        int left = 2 * i + 1;
        int right = 2 * i + 2;

        if (left < n && arr[left] > arr[largest]) {
            largest = left;
        }

        if (right < n && arr[right] > arr[largest]) {
            largest = right;
        }

        if (largest != i) {
            int swap = arr[i];
            arr[i] = arr[largest];
            arr[largest] = swap;

            heapify(arr, n, largest);
        }
    }

    public static void main(String[] args) {
        int[] arr = {38, 27, 43, 3, 9, 82, 10};
        heapSort(arr);
        System.out.println("Heap Sort 결과: " + Arrays.toString(arr));
    }
}

퀵 정렬

• 임의의 기준 값을 정하고 그 값을 기준으로 좌우로 분할하며 정렬하는 방식
• 시간 복잡도 O(n^2)

import java.util.Arrays;

public class QuickSort {
    public static void quickSort(int[] arr, int low, int high) {
        if (low < high) {
            int pi = partition(arr, low, high);

            quickSort(arr, low, pi - 1);
            quickSort(arr, pi + 1, high);
        }
    }

    private static int partition(int[] arr, int low, int high) {
        int pivot = arr[high];
        int i = (low - 1);

        for (int j = low; j < high; j++) {
            if (arr[j] <= pivot) {
                i++;

                int temp = arr[i];
                arr[i] = arr[j];
                arr[j] = temp;
            }
        }

        int temp = arr[i + 1];
        arr[i + 1] = arr[high];
        arr[high] = temp;

        return i + 1;
    }

    public static void main(String[] args) {
        int[] arr = {38, 27, 43, 3, 9, 82, 10};
        quickSort(arr, 0, arr.length - 1);
        System.out.println("Quick Sort 결과: " + Arrays.toString(arr));
    }
}

트리 정렬

• 이진 탐색 트리를 만들어 정렬하는 방식
• 시간 복잡도 O(nlogn)

import java.util.ArrayList;

class TreeNode {
    int value;
    TreeNode left, right;

    public TreeNode(int item) {
        value = item;
        left = right = null;
    }
}

class TreeSort {
    TreeNode root;

    public void insert(int value) {
        root = insertRec(root, value);
    }

    private TreeNode insertRec(TreeNode root, int value) {
        if (root == null) {
            root = new TreeNode(value);
            return root;
        }
        if (value < root.value) {
            root.left = insertRec(root.left, value);
        } else if (value > root.value) {
            root.right = insertRec(root.right, value);
        }
        return root;
    }

    public void inorderRec(TreeNode root, ArrayList<Integer> sortedList) {
        if (root != null) {
            inorderRec(root.left, sortedList);
            sortedList.add(root.value);
            inorderRec(root.right, sortedList);
        }
    }

    public static void main(String[] args) {
        int[] arr = {38, 27, 43, 3, 9, 82, 10};
        TreeSort tree = new TreeSort();
        
        for (int num : arr) {
            tree.insert(num);
        }

        ArrayList<Integer> sortedList = new ArrayList<>();
        tree.inorderRec(tree.root, sortedList);

        System.out.println("Tree Sort 결과: " + sortedList);
    }
}

기수 정렬

• 낮은 자리 수부터 정렬하는 방식
• 각 원소 간의 비교 연산을 하지 않아 빠른 대신, 기수 테이블을 위한 메모리 필요
• 시간 복잡도 O(dn)

계수 정렬

• 숫자끼리 비교하지 않고 카운트를 세서 정렬하는 방식
• 카운팅을 위한 메모리 필요
• 시간 복잡도 O(n+k)

셸 정렬

• 삽입 정렬의 약점 보완한 정렬 방식
  • 오름차순, 내림차순으로 구성된 데이터에 대해서는 앞의 데이터와 하나씩 비교하며 모두 교환을 해야한다.
• 이전의 모든 데이터와 비교하지 않고 일정 간격을 두어 비교
• 시간 복잡도 O(n^2)