최소 신장 트리
최소 신장 트리(minimum spanning tree)란 그래프에서 모든 노드를 연결할 때 사용된 엣지들의 가중치의 합을 최소로 하는 트리 -> 크루스칼, 프림 알고리즘이 있음
예시
다음과 같은 도시와 길이 있다고 생각해보자
도시: A, B, C, D
길(가중치)
A-B: 1
A-C: 3
B-C: 2
B-D: 4
C-D: 5
모든 도시를 연결하는 여러 방법이 있다. 예를 들어,
A-B-C-D (가중치: 1 + 2 + 4 = 7)
A-B-D-C (가중치: 1 + 4 + 5 = 10)
이 중에서 가장 적은 가중치를 가진 연결 방법이 최소 신장 트리이다.
특징
-
모든 노드가 연결되어 있어야 한다.
-
끊어진 도시가 하나라도 있으면 안된다.
-
사이클이 없어야 한다.
- 예를 들어, A-B-C-A처럼 같은 길을 돌아오는 루프는 없어야 한다.
-
가중치의 합이 최소여야 한다.
- 가장 적은 비용으로 연결할 수 있는 방법을 찾는 게 핵심
-
간선의 개수는 항상 N-1.
- 도시(노드)의 개수가 N개라면, MST에 포함된 길(간선)은 항상 N-1개이다.
-
시간복잡도 : O(ElogE)
최소 신장 트리 과정
-
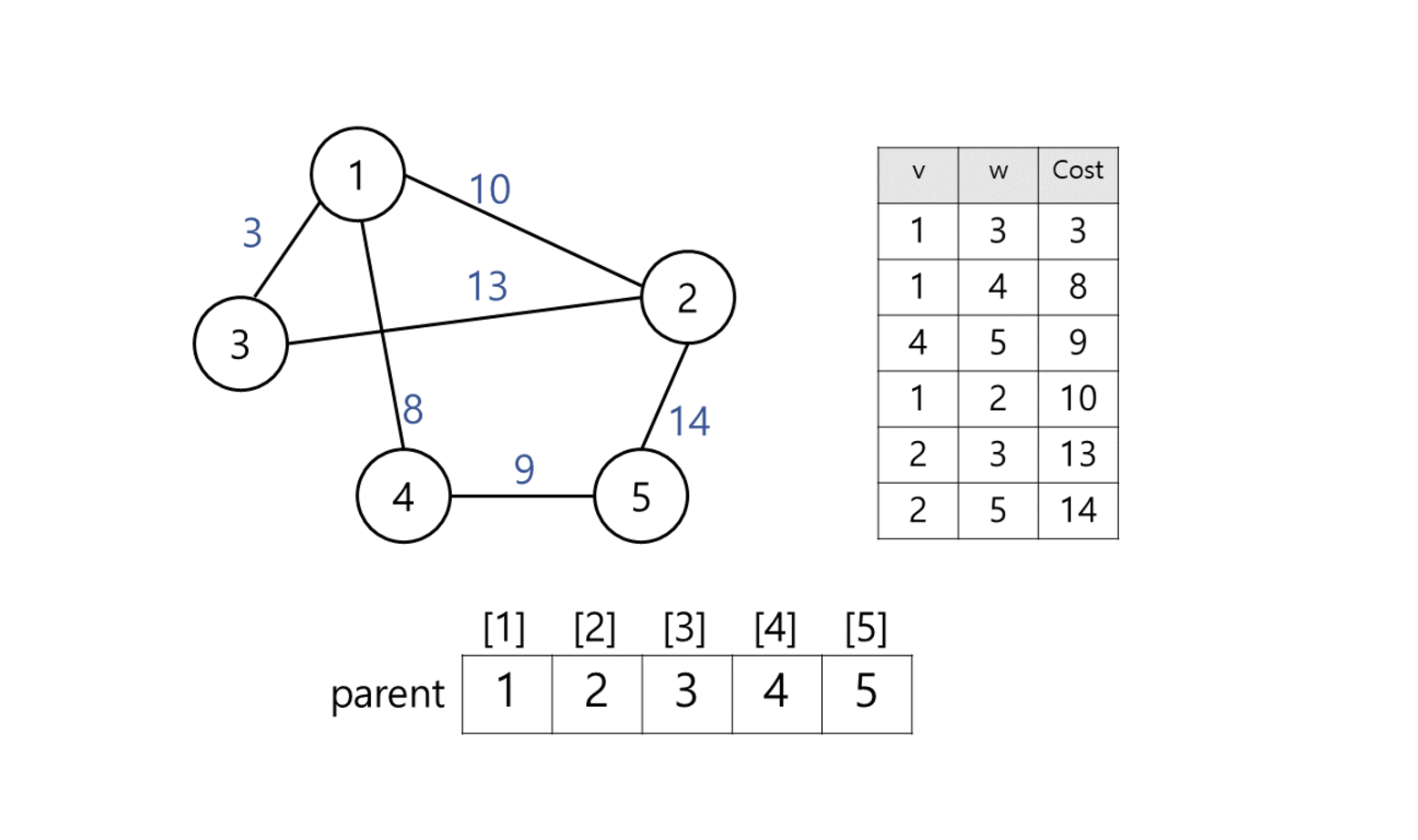
엣지 리스트로 그래프를 구현, 유니온 파인드 리스트 초기화하기
왜 유니온 파인드가 쓰이는가? -> 싸이클 판별을 위해서 -
엣지 리스트에 담긴 그래프 데이터를 가중치 기준으로 오름차순 정렬을 한다.
-
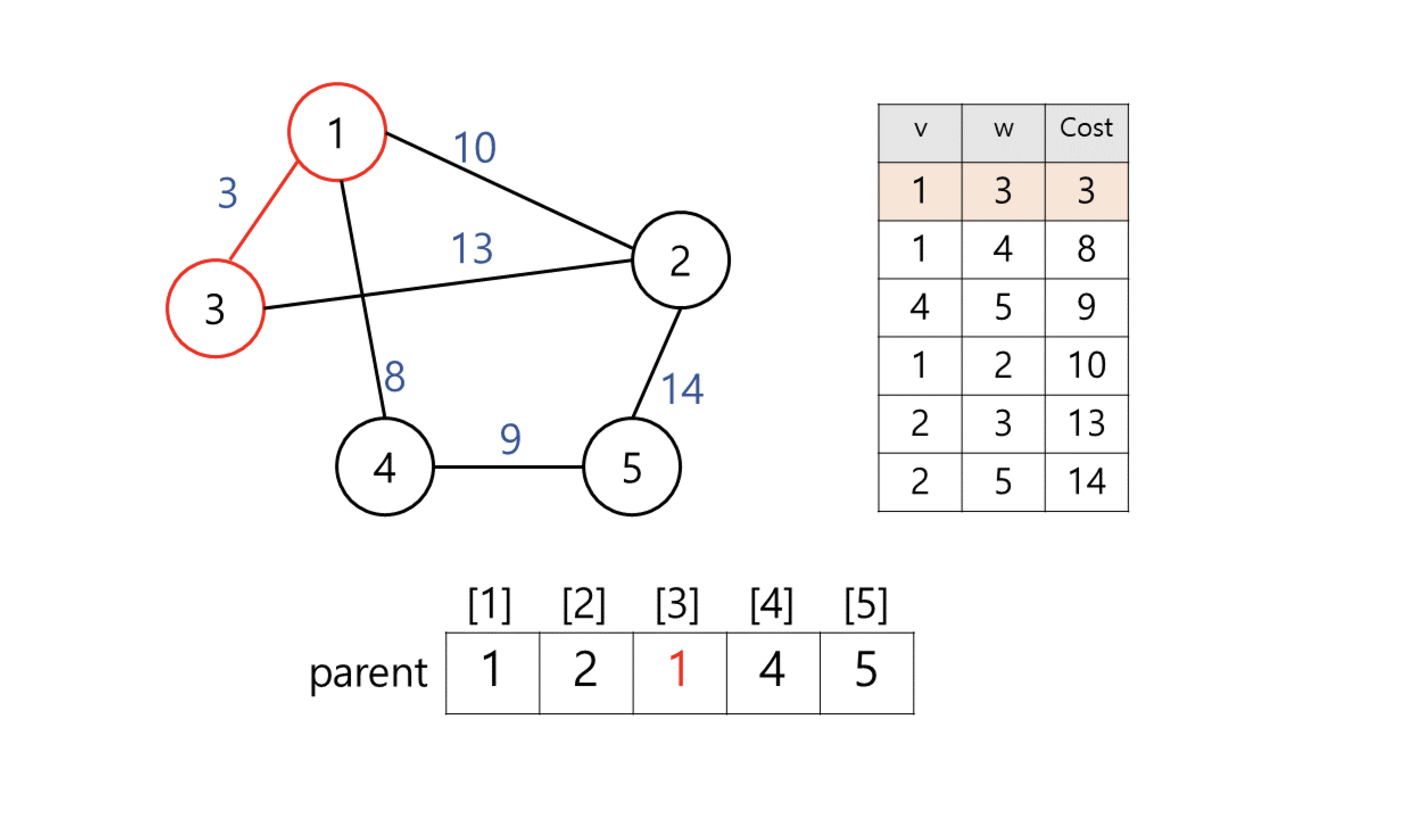
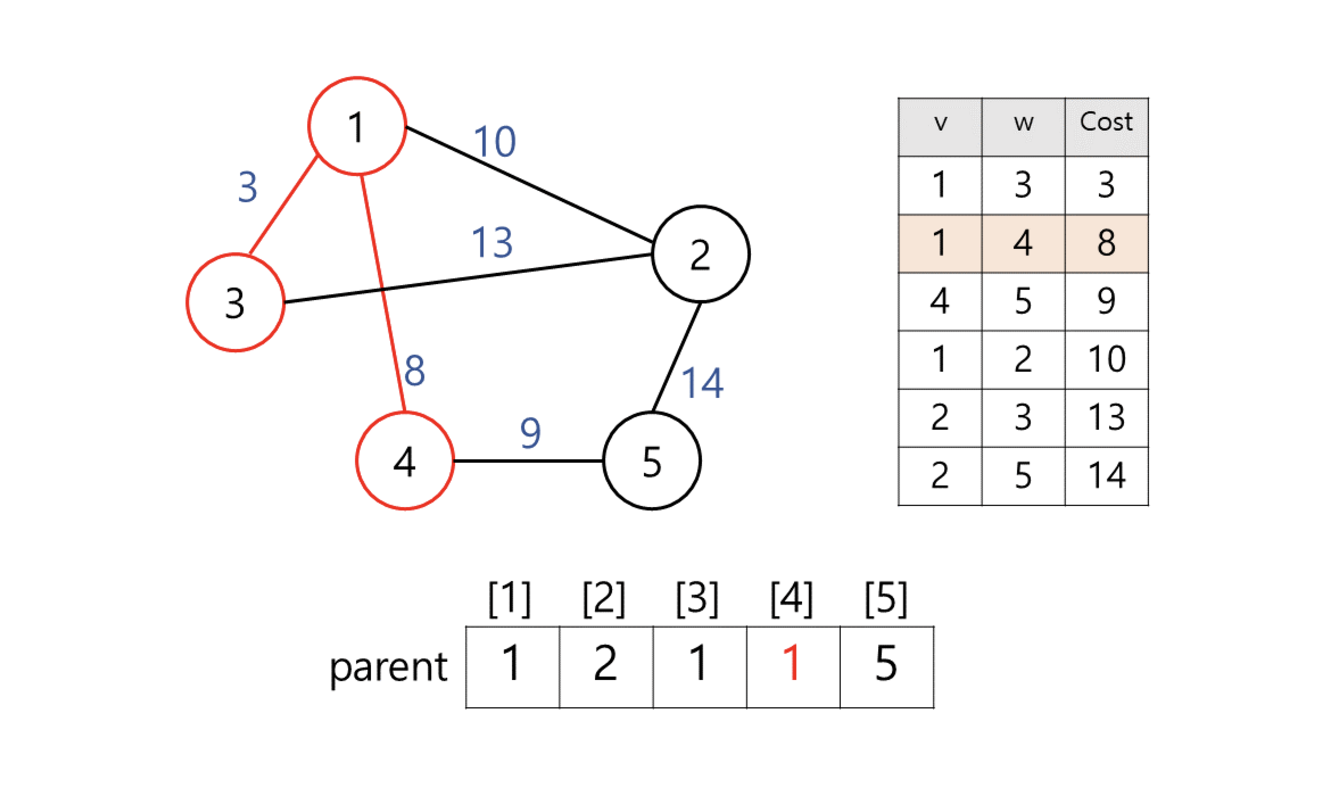
가중치가 낮은 엣지부터 연결을 시도한다.
두 노드의 대표 노드가 다를 경우에만 연결 -> 대표 노드가 같다면 두 노드를 연결했을 때 싸이클이 만들어진다. -
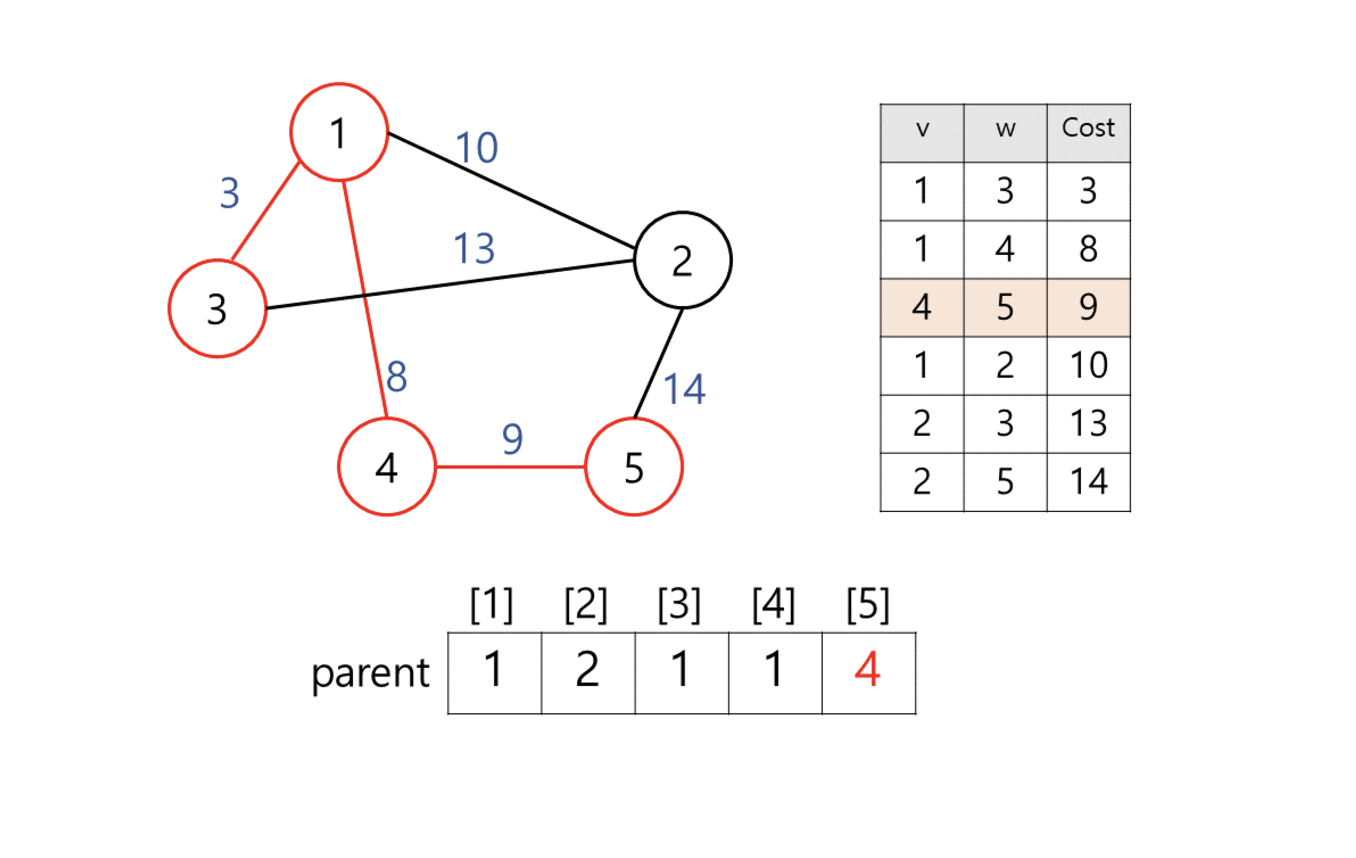
과정3 반복
-
엣지의 개수가 N-1개가 되면 종료하고 총 엣지 비용 출력
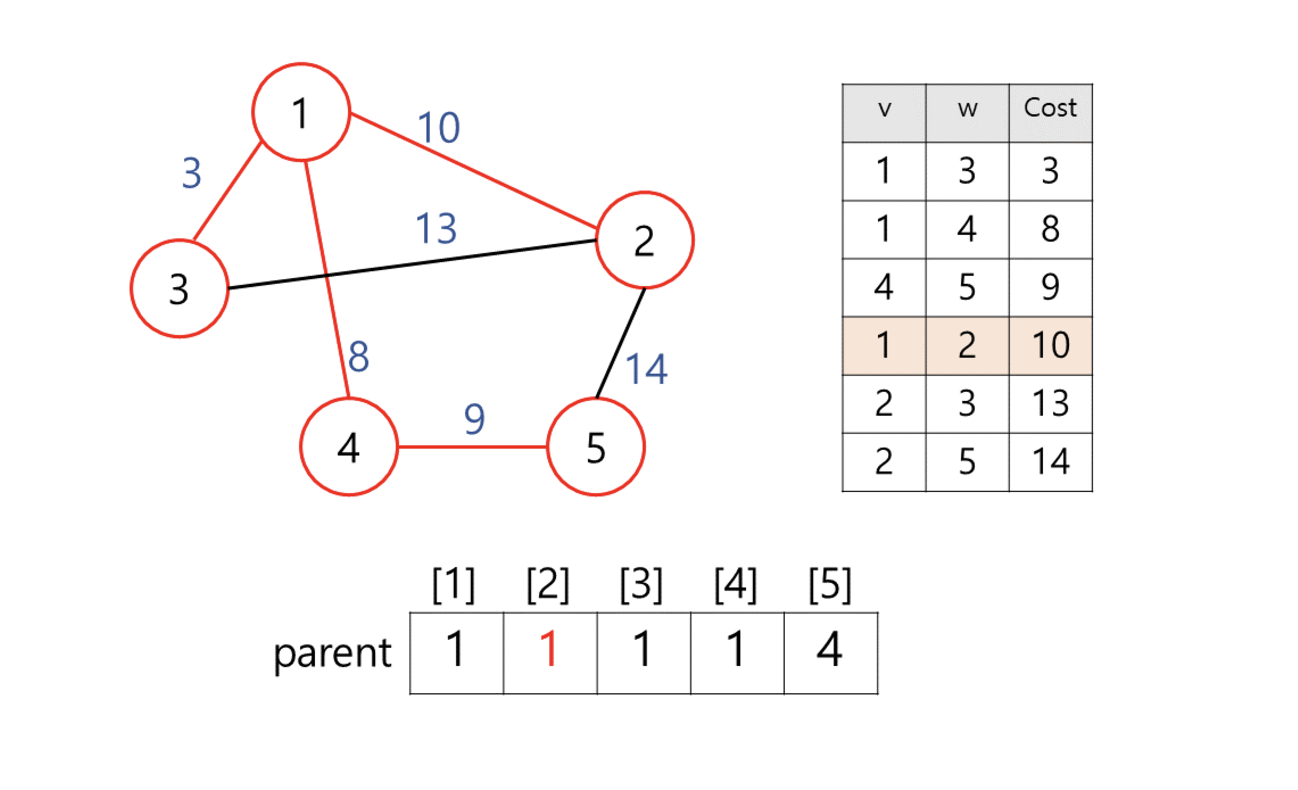
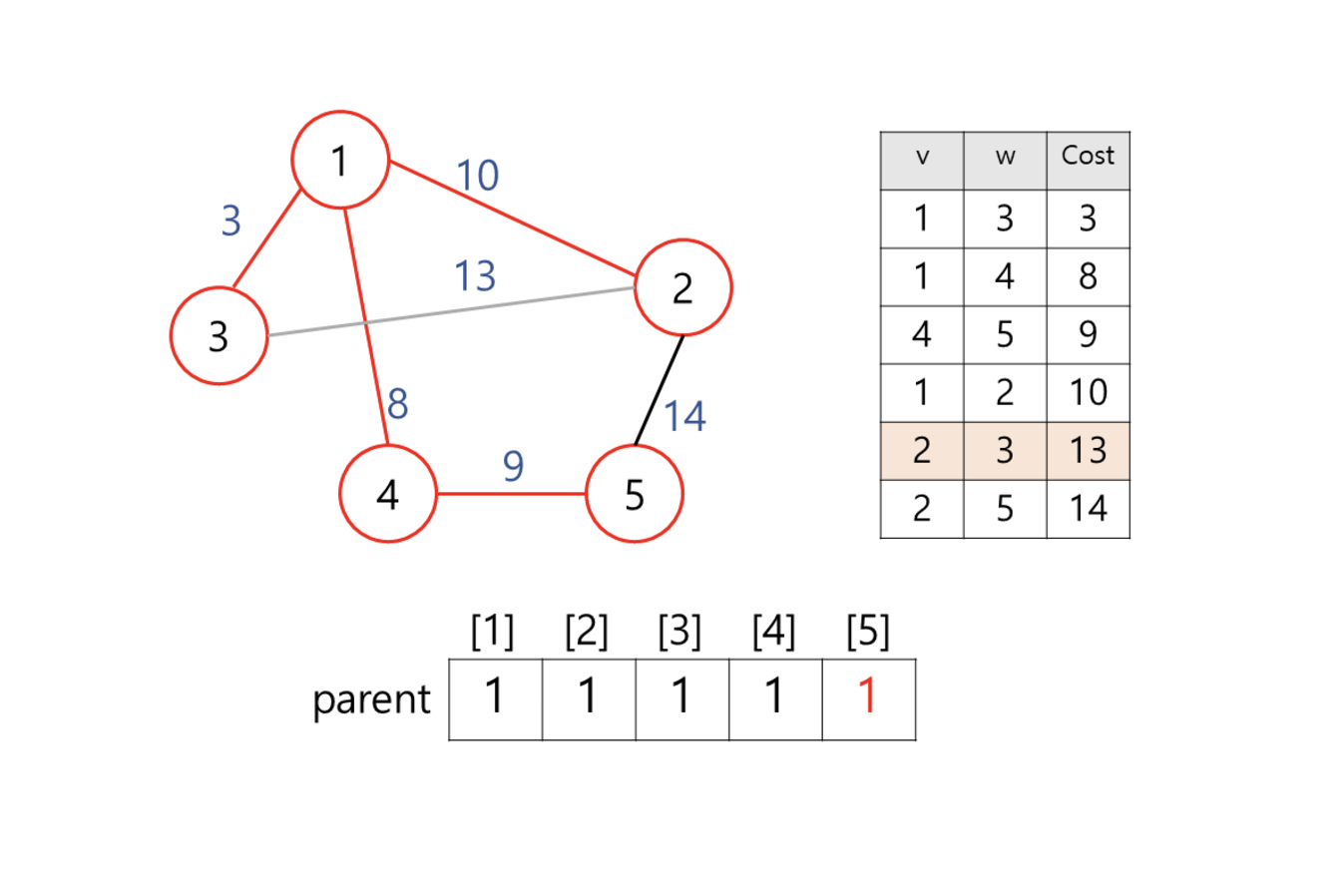
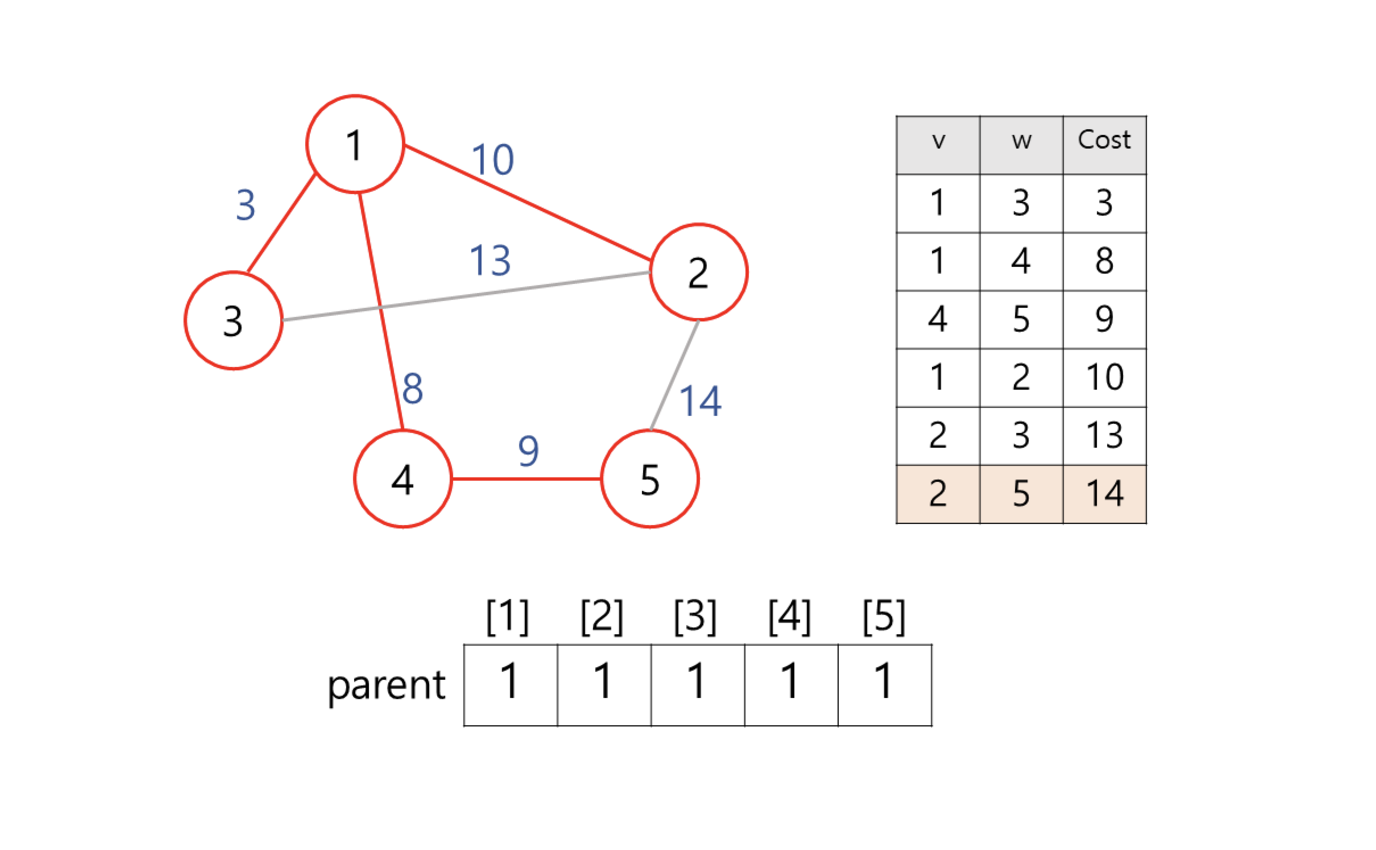
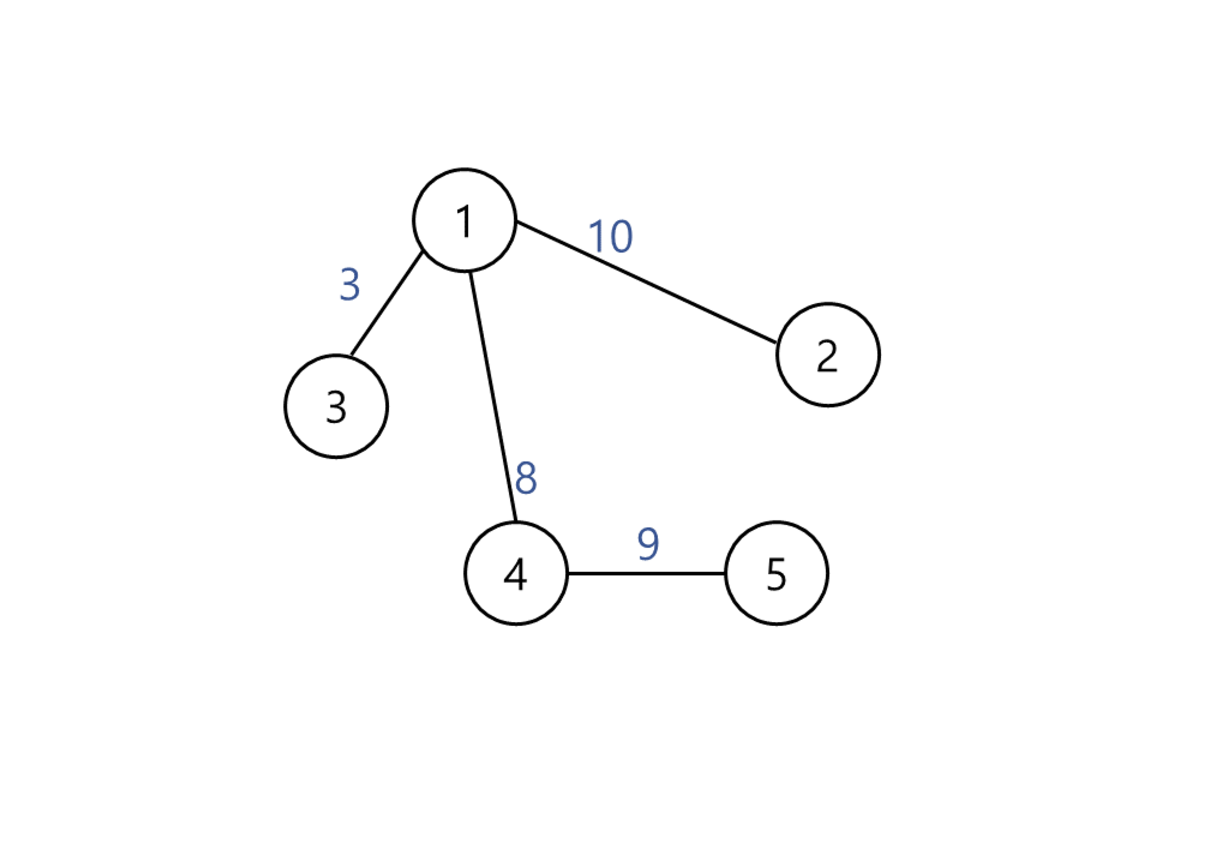
백준 1197
import java.io.*;
import java.util.*;
public class Main {
//엣지리스트 생성
static int[][] graph;
//부모 노드
static int[] parent;
//최종값
static int total;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
int V = Integer.parseInt(st.nextToken());
int E = Integer.parseInt(st.nextToken());
graph = new int[E][3];
for(int i=0; i<E; i++){
st = new StringTokenizer(br.readLine());
graph[i][0] = Integer.parseInt(st.nextToken());
graph[i][1] = Integer.parseInt(st.nextToken());
graph[i][2] = Integer.parseInt(st.nextToken());
}
Arrays.sort(graph, Comparator.comparingInt(o -> o[2]));
parent = new int[V+1];
for(int i=1; i<V+1; i++){
parent[i] = i;
}
kruskal(graph, parent);
}
static void kruskal(int[][] graph, int[] parent){
total = 0;
for(int i=0; i<graph.length; i++){
if(find(parent, graph[i][0]) != find(parent, graph[i][1])){
total += graph[i][2];
union(parent, graph[i][0], graph[i][1]);
}
}
System.out.println(total);
}
static void union(int[] parent, int i, int j){
i = find(parent, i);
j = find(parent, j);
if(i<j){
parent[j] = i;
}else{
parent[i] = j;
}
}
static int find(int[] parent, int i){
if(parent[i] != i){
parent[i] = find(parent, parent[i]);
}
return parent[i];
}
}