컴퓨터는 우리가 사용하는 10진수를 사용하지 않고, 2진수를 사용한다.
컴퓨터가 전기적 신호로 의미를 전달할 수 있는 최소 단위는 (ON/OFF)이기 때문이다.
만약 컴퓨터가 10진수 체계를 사용한다면 10단계의 신호의 구분이 필요하게 될 것이다.
목차
1. 논리연산
2. 2진수의 덧셈
3. 2진수의 부호 (음수 표현)
4. 부동 소수
5. 비트 그룹의 이름
6. 유니코드와 UTF-8
7. Base64 인코딩
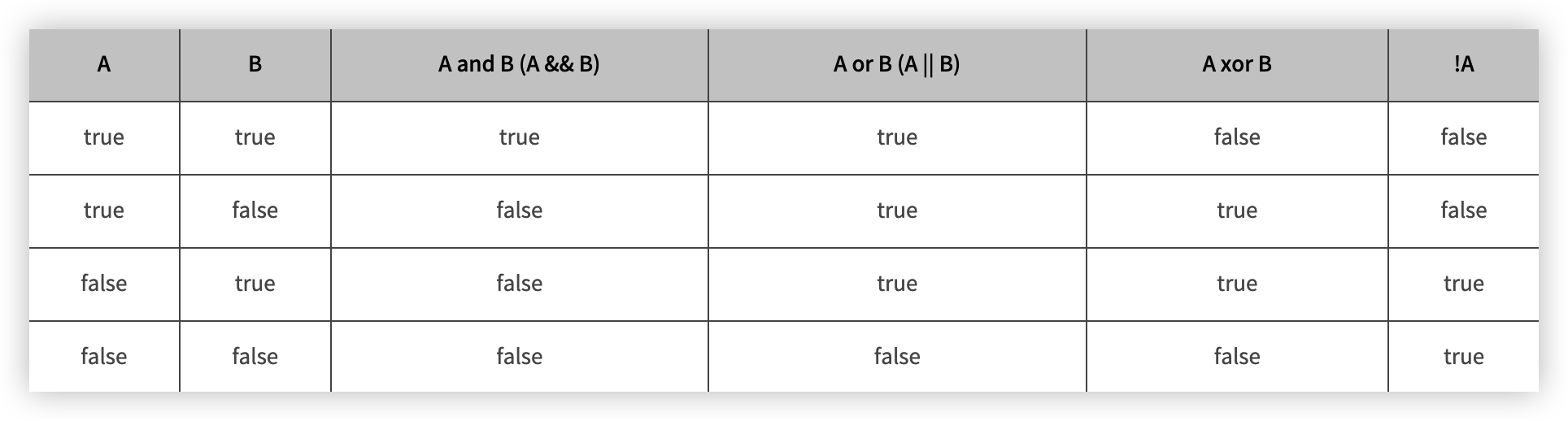
논리 연산
- AND 연산
- OR 연산
- XOR 연산
- NOT 연산
2진수 덧셈
2 진수의 덧셈을 논리 연산으로도 구현할 수 있다.
덧셈을 논리 연산으로 표현하면 합과 자리올림으로 나타낼 수 있다.
두 비트를 서로 더한 결과는 두 비트를 XOR 한 값과 같고,
올림은 두 비트를 AND 한 값과 같다.
A = 0011
B = 0101
합 (XOR) = 0110
올림 (AND) = 0001
총 A+B = 1000
2진수의 음수 표현
1. 부호 있는 절대치
가장 간단하게 음수를 표현하면서 사람에게 친화적인 방식으로 음수를 표현하는 방식
MSB(Most Significant Bit)가 0 이면 양수, 1이면 음수.
3 = 0011
-3 = 1011
부호 있는 절대치 문제점 :
컴퓨터의 주 기능인 연산을 하지 못한다.
예)
0001(1) + 1001(-1) = 1010 => -2 라는 결과가 나온다.
따라서 부호 있는 절대치 음수는 컴퓨터에선 사용하지 않는다.
2. 1의 보수 (1's Complement)
음수를 표현하기 위해 양수에 NOT 비트연산을 하는 방법이다.
모든 비트를 반전 시킨다. 0 -> 1, 0 -> 1
예)
10 진수 33 표현
2진수 => 1000001. 양수이므로 MSB에 0을 붙여줘서 '0' + '1000001' 이다.
10 진수 -33 표현
2진수 => 0111110. 음수이므로 '1' + '0111110' 로 표현해준다.
1의 보수의 문제점 :
연산이 가능하지만 과정이 조금 복잡 = 컴퓨터 자원을 낭비
예 )
5 + (-1) 을 해보겠다.
5 = 0101
-1 = 1110
0101 + 1110 = 10011
4bit 였는데 5bit가 되어버렸.
이런 경우 carry가 발생했다고 한다. 즉 잉여로 올림이 발생하면 carry bit.
1의 보수 연산에서는 carry 를 원래 수에 더해주어야 연산이 끝난다.
즉 10011 => 0011 + 1 => 0100
이렇게 5 -1 은 4가 제대로 출력되었다.
3. 2의 보수 (2's Complement)
1의 보수를 구한 후 1을 더해주는 방법으로,
모든 비트를 반전시킨 후 +1 을 해준다.
10진수 33 => 1000001. 양수이므로 MSB 에 '0' 추가. => 01000001.
10진수 -33 => 10111110 에서 +1 => 10111111
만약 2진수에서 다시 10진수로 변환하기 위해서는
2진수 '1011111' 중 MSB 를 분리. '1011111' -> '1', '011111'
그 후 1를 뺀 후 '011111' - '000001' => '011110' , 반전 시킨다 '100001'.
100001 은 10진수로 33이고 MSB 는 1(음수)이 였으니 -33 이다.
대부분의 컴퓨터 부호 연산에서는 2의 보수를 사용 :
1의 보수에 비해 연산이 간단하다는 장점이 있다.
carry 발생 시 버려버리면 된다.
예 ) 5 + (-1)
0101(5) + 1111(-1) => 10100.
맨 앞자리인 carry 인 '1'을 버려주면 0100 으로 4가 제대로 출력되었다.
비트 그룹의 이름
미터법에서
킬로(kilo) 는 1천
메가(mega) 는 100만
기가(giga) 는 10억
테라(tera) 는 1조를 뜻한다.
이와 비슷하게
킬로비트(kilobit) 는 1000에 가장 가까운 수인 2^^10 => 1024
메가비트(megabit) 는 2^^20
기가비트(gigabit) 는 2^^30
테라비트(terabit) 는 2^^40
유니코드와 UTF-8
Unicode
아스키는 영어를 표현하는데 필요한 모든 문자와 제어 문자를 담고 있다.
하지만 시간이 지나서 그 밖의 언어를 지원해야하는 필요가 늘었는데, 각 나라들은 아스키코드에 각 나라마다의 언어를 더해서 그 나라의 표준을 만들었다. (일본은 아스키코드 + 일본언어 등을 해 JIS (Japenese Industrial Standards 를 만들고, 한국 등은 한국어 표준인 (KS C 5601) 등을 만들었다)
이렇게 각 나라마다 다른 표준이 존재했더니 다른 나라 홈페이지에 들어갔더니 글자가 와장창 깨지는 문제가 발생했다. 이를 해결할 솔루션으로 Unicode 라는 새로운 표준을 만들어 전 세계의 모든 문자를 컴퓨터에서 표현할 수 있도록 만들었다.
유니코드를 인코딩하는 방식은 UTF-8 과 UTF-16이 대표적이다.
UTF-8 (Unicode Transformation Format - 8bit)
정의 : UTF-8은 풀네임에서도 알 수 있듯이 유니코드를 8bit(1byte)를 기준으로 Encoding 하는 방식이다.
특징 :
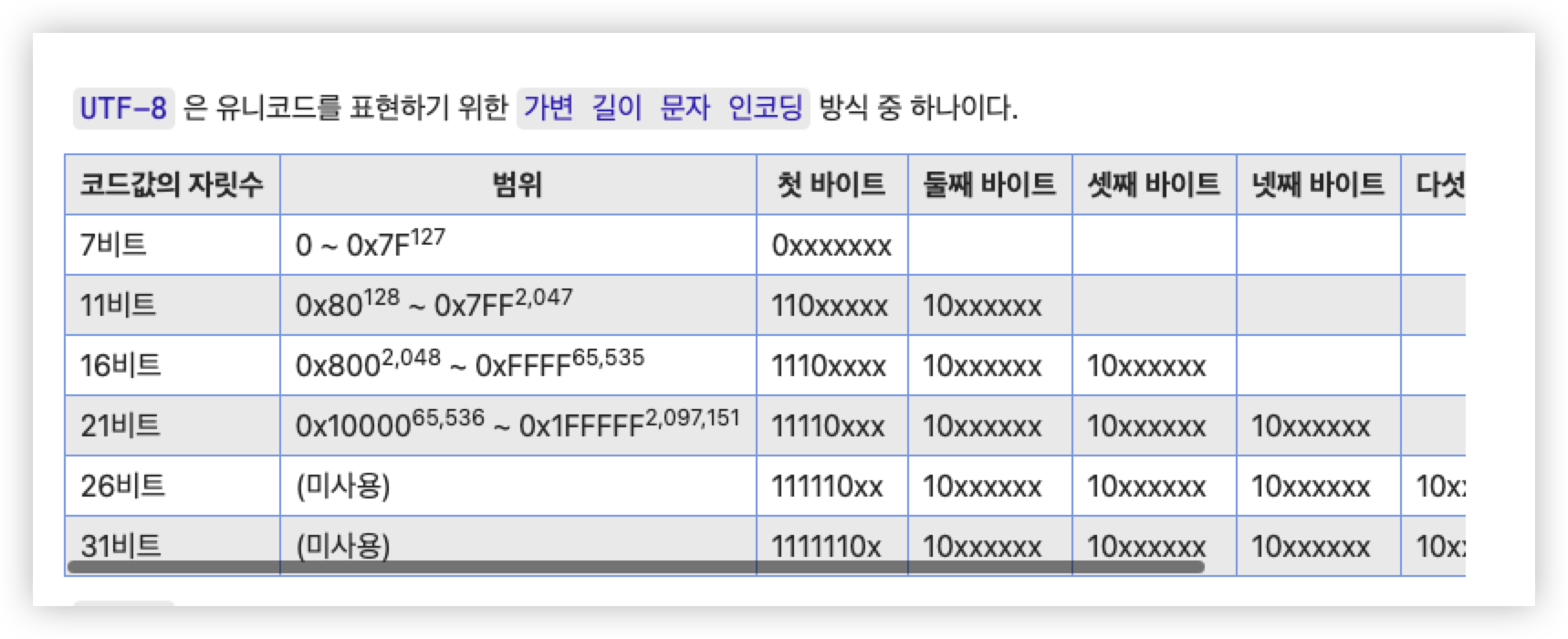
UTF-8은 가변 인코딩 방식이다.
가변 길이라는게 쉽게 말하면 인코딩 된 값이 1~4byte 의 값을 동적으로 얻는다는 말이다.
예를 들면
영어 알파벳 'A'의 유니코드 코드 포인트는 U+0041 이다. 이진 표현은 1000001 이다.
즉 A는 7비트로 표현되므로, UTF-8 1byte로 표현이 가능하다.
A는 UTF-8 인코딩으로 다음과 같이 표현된다.
01000001. 즉 맨 앞자리의 0은 UTF-8 1byte 로 표현했다는 말이다.
만약 "코" 라는 문자를 UTF-8로 표현하면, "코"는 유니코드 U+CF54 (이진 표현 = 1100-1111-0101-0100)로 표현될 수 있고 UTF-8 3bytes로 표현해야한다.
즉
1110xxxx 10xxxxxx 10xxxxxx // (3bytes의 식별자들이다. 가장 하위 byte의 마지막 x부터 채워 넣는다
11101100 10111101 10010100
즉 가변을 다시 설명하자면 "A"를 표현할 때 1byte로도 표현하는데에 충분하지만,
1byte 만으로는 세상에 있는 모든 글자를 표현하는게 불가능하다. ("코"라는 글자만 봐도 알 수 있듯이)
그래서 만약 세상에 있는 글자가 모두 4byte 로 표현 가능하다고 가정했을 때,
"A"는 00000000 00000000 00000000 01000001 로 표현될 수 있는데 이때 0으로 표현된 3byte 들은 너무 비효율적이니 가변으로 문자를 표현할 때 1byte만으로도 표현이 가능하다면 4byte로 표현하는 것이 아닌, 1byte로 가변적으로 표현하자는 것이 UTF-8 의 핵심이다.
Base64 인코딩
정의 : Base64 Encoding은 Binary Data를 Text로 변경하는 Encoding이다.