목차
1. 데이터 정규화
- 데이터 정규화를 하는 이유
- 정규화
- 표준화
- 정규화와 표준화 차이
- Batch Normalization
- Batch Normalization 을 사용했을 때 장점
- Internal Convariance Shift (ICS)
-Convaiate Shift
-Internal Convariate Shift - Batch Normalization 의 자세한 설명
-정의
-Batch Normalization 수식 및 방법
-추론(Inference) 시의 Batch Normalization
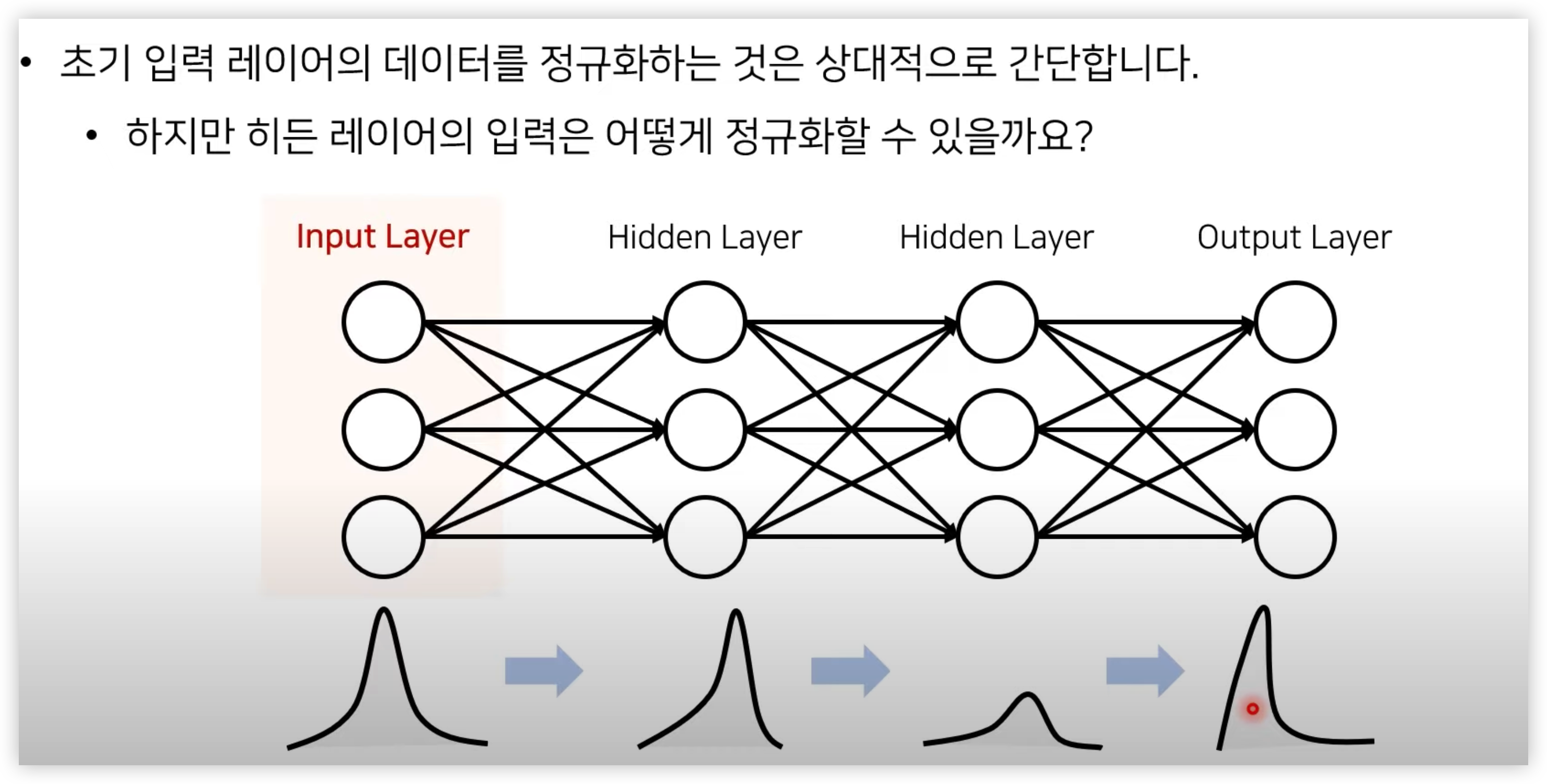
우선 왜 데이터를 정규화 해야할까 ?
데이터 정규화 (Normalization) 또는 표준화(Standardization)을 하는 이유
데이터 컬럼 별 단위를 통일 시켜준다고 생각하면 편안하다.
컬럼별로 시간, km, kg 등 다양한 단위를 가지는데 이러면 직접적인 비교가 불가능하다.
예를 들어 "넌 180cm 인데 난 80kg 이니깐 내가 더 몸이 좋아" 라고 한다면 상대방이 날 이상한 사람으로 생각할 것이다. 또는 "난 토익 300(990점만점)점인데 넌 학교 점수가 100점(100점만점)이니 내가 더 영어를 잘하네" 라고 한다면 역시 이상하게 생각할 것이다.
이처럼 다른 성격의 데이터들을 비교하는 것이 말이 안되므로 이를 극복하기 위해 "정규화" 또는 "표준화"를 해줘서 서로를 비교할 수 있게 해줄 수 있다
정규화 또는 표준화의 목표
데이터셋의 numerical value 범위의 차이를 왜곡하지 않고 공통 척도로 변경하는 것
만약 머신러닝에서 데이터의 범위(scale)가 다르다면 ?
예를 들어 X1은 0 부터 1 사이의 값을 갖고
y 는 100 부터 1000 사이의 값을 갖는다고 가정한다면
X 특성은 y 를 예측하는데 큰 영향을 주지 않는 것으로 생각할 수 있다.
또 다른 예로는 나이와 재산이라는 특성이 있을 때, 재산의 값이 나이보다 훨씬 크기 때문에 재산에 치중한 학습을 하게 된다.
즉 특성별로 데이터의 범위가 다르면 머신러닝이 잘 학습되지 않는다.
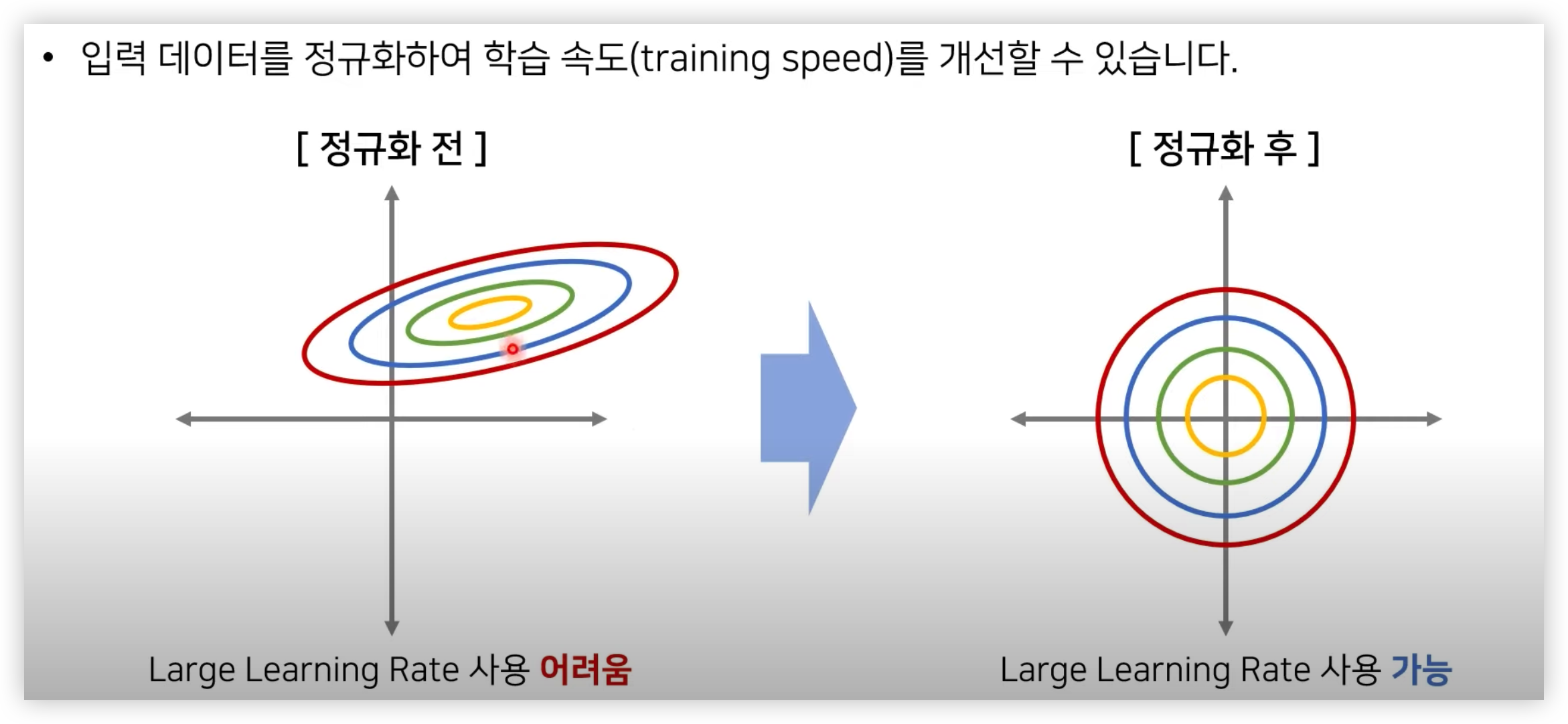
(추가적으로 말한다면 두 특성 데이터가 범위가 달라도 학습은 될 수 있겠지만, learning rate 를 아주 작게해야하기 때문에 학습시간이 굉장히 오래 걸릴 것이다.
왜냐하면 정규화전 그림에서 learning rate 을 조금만 크게 하면 x 축은 global minima 에 접근할 수 있겠지만, y축은 위로 발산할 수도 있기 때문이다.)
(머신러닝과 정규화에 대한 내용 참고 - https://light-tree.tistory.com/132 )
표준화 또는 정규화를 머신러닝에서 사용했을 때 장점
local minima 문제에 빠지는 가능성을 줄이기 위해 사용한다.
아래 그림처럼 Loss 값의 최저점을 찾을 때 그래프 전체를 이해하지 못하여 lobal minima 지점을 찾지 못하고 Local Optimum 에 머물러 있게 되는 문제가 발생 된다.
이러한 문제점을 정규화 하여 그래프를 왼쪽에서 오른쪽으로 만들어, local minima 에 빠질 수 있는 가능성을 낮춘다.
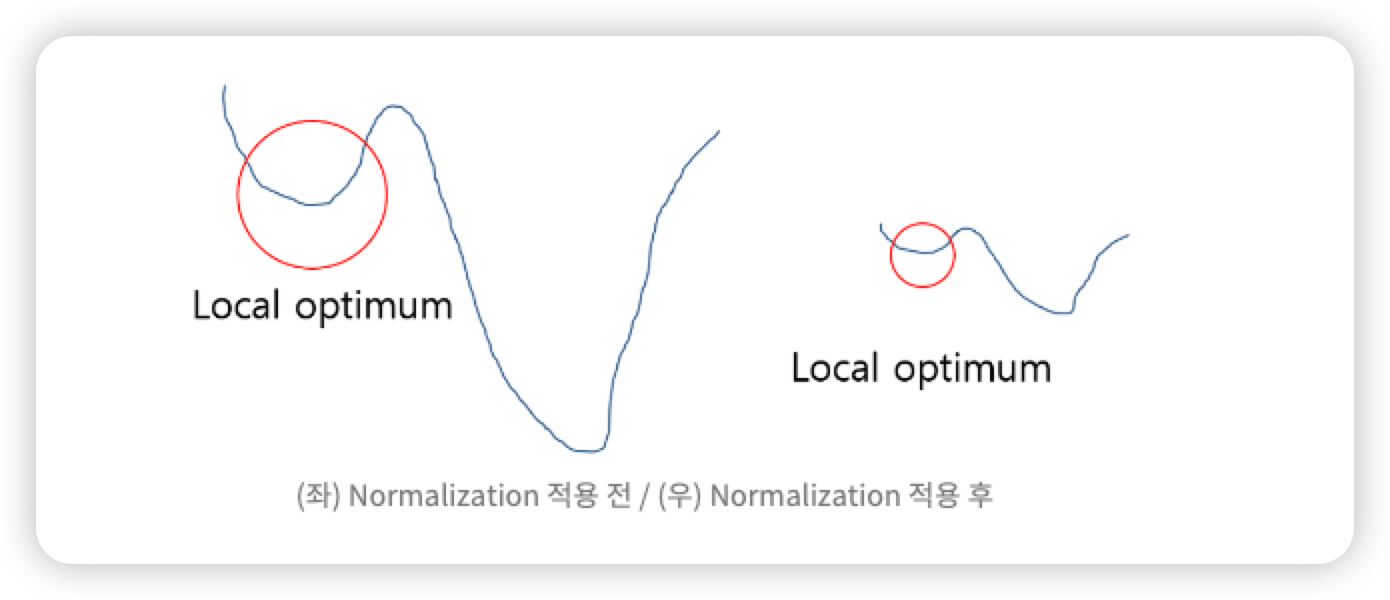
(위 만약 머신러닝에서 데이터의 범위(scale)가 다르다면 ? 같은 내용이다)
자세하게 정규화와 표준화를 한번 알아보자
정규화 (Normalization)
모든 피처가 [0,1] 사이에 위치하도록 데이터를 변경한다.
2차원 데이터셋일 경우에는 모든 데이터가 x축의 0과 1, y축의 0과 1 사이의 사각 영역에 담기게 된다.
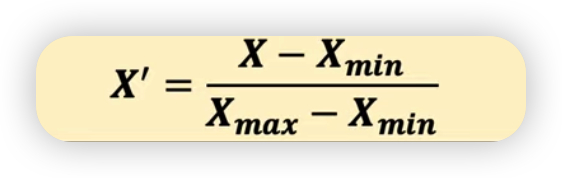
( 그림1 - Normalization 식 )

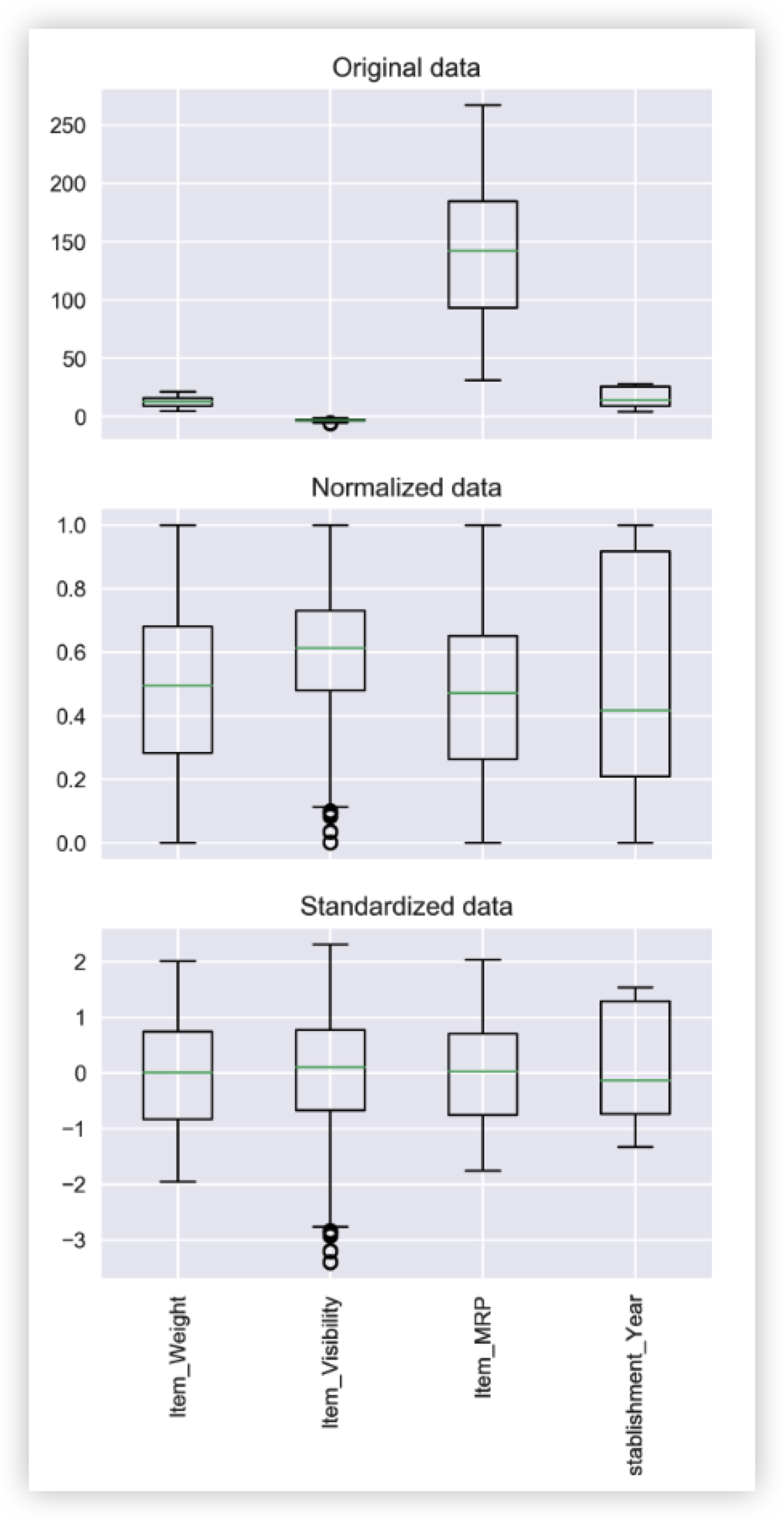
( 그림2 - Normalization 을 진행했을 때의 전 후 결과 )
표준화 (Standardization)
표준 정규 분포의 속성을 갖도록 값이 재조정 되는 것.
즉 평균이 0, 분산이 1 이 되도록 값을 조정 시킨다.
( 그림3 - Standardization 식)
여기서 뮤는 평균이고 시그마는 평균으로부터의 표준편차이다. 표본의 표준 점수(Z-score)는 다음과 같이 계산된다.
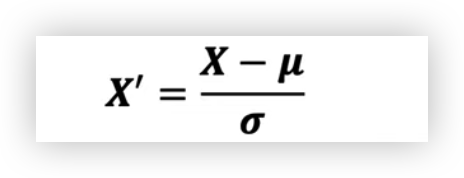
( 그림4 - Standardization 을 진행했을 때의 전 후 결과)

(표준화 방법은 이상치(outlier) 를 파악할 수 있는 좋은 방법이다.
Z-score 를 구함으로써 데이터가 평균으로부터 얼마나 떨어져있는지 구한 다음, 특정 범위를 벗어난 데이터는 이상치로 간주해 제거할 수 있다. 예를 들면 표준화한 Z값이 간단히는 +-2시그마 안에 있으면 95% 신뢰구간 내에 있는 것이므로, 이 데이터만 선택하게 되면 이상치를 제거할 수 있다.)
Normalization 과 Standardization 차이
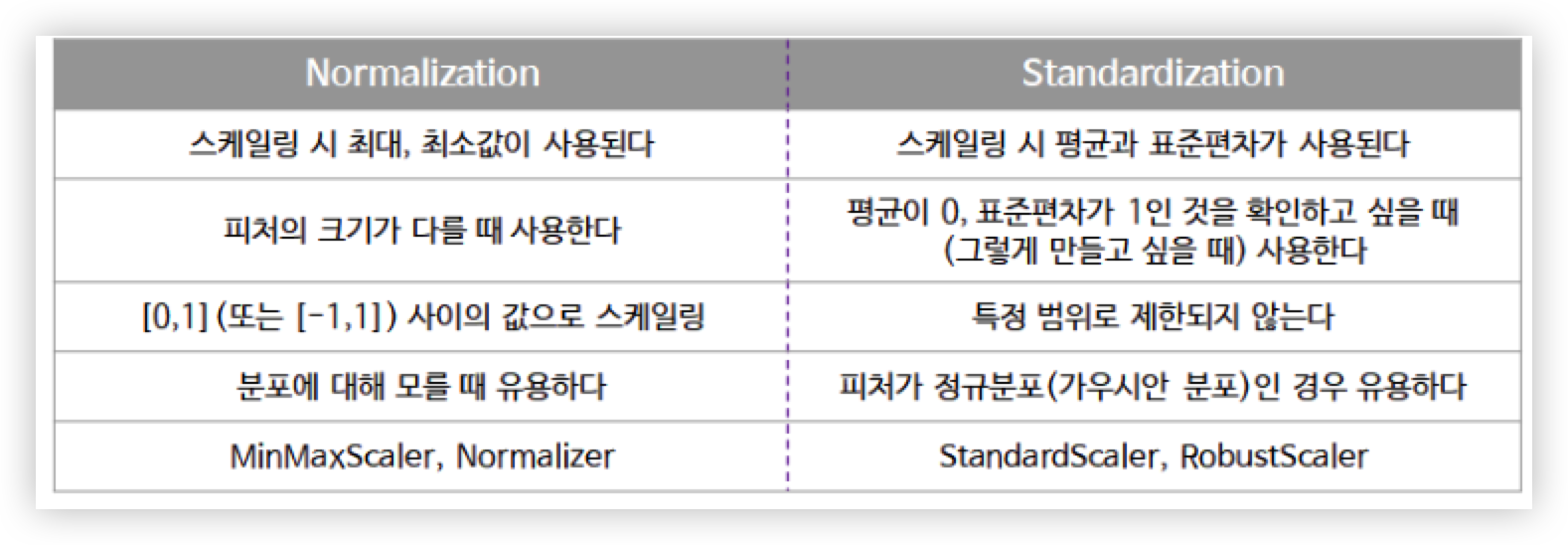
표준화 또는 정규화 중 어떤 기법을 써야할 지에 대한 자료 :
https://hleecaster.com/ml-normalization-concept/
Batch Normalization (BN)
Batch Norm 을 사용했을 때의 장점과 사용하는 이유
- 학습 속도(training speed)를 빠르게 할 수 있다. (학습률을 높게 설정할 수 있기 때문)
- 가중치 초기화(weight initialization)에 대한 민감도를 감소시킨다.(학습을 할 때마다 출력 값을 정규화하기 때문)
- Overfitting 위험을 줄일 수 있다. (드럽아웃 같은 기법 대체 가능)
- Gradient Vanishing 문제 해결
여기서 왜 Batch Normalization 을 사용하면 학습속도가 빨라 질까 ?
학습 속도 가속화라는 것은 iteration, epoch 진행 속도가 향상 된다는 뜻이 아니라,
초기 파라미터 값에 대한 dependency가 줄어 Large Learning Rate 를 설정할 수 있기 때문에 결과적으로 빠른 학습이 가능하다.
즉 기존 방법에서는 Learning Rate 를 높게 잡을 경우 gradient 가 vanish/explode 하거나 local minima에 빠지는 경향이 있었는데 이는 scale 때문이었으며, Batch Normalization을 사용할 경우 propogation 시 파라미터의 scale 에 영향을 받지 않게 되기 때문에 Learning Rate 를 높게 설정할 수 있는 것이다.
Batch Normalization 에 대해 자세히 들어가기 전에 앞서 Batch Normalization 의 탄생된 역사를 살펴보자.
Batch Normalization 논문의 저자는 학습에서 불안정화가 일어나는 이유를 "Internal Convairance Shift"라고 주장하는데, 이를 한번 자세히 알아보자.
Covariate Shift
Covariate Shift 는 공변량 변화라고하며, 입력 데이터의 분포가 학습할 때와 테스트할 때 다르게 나타나는 현상을 말한다.
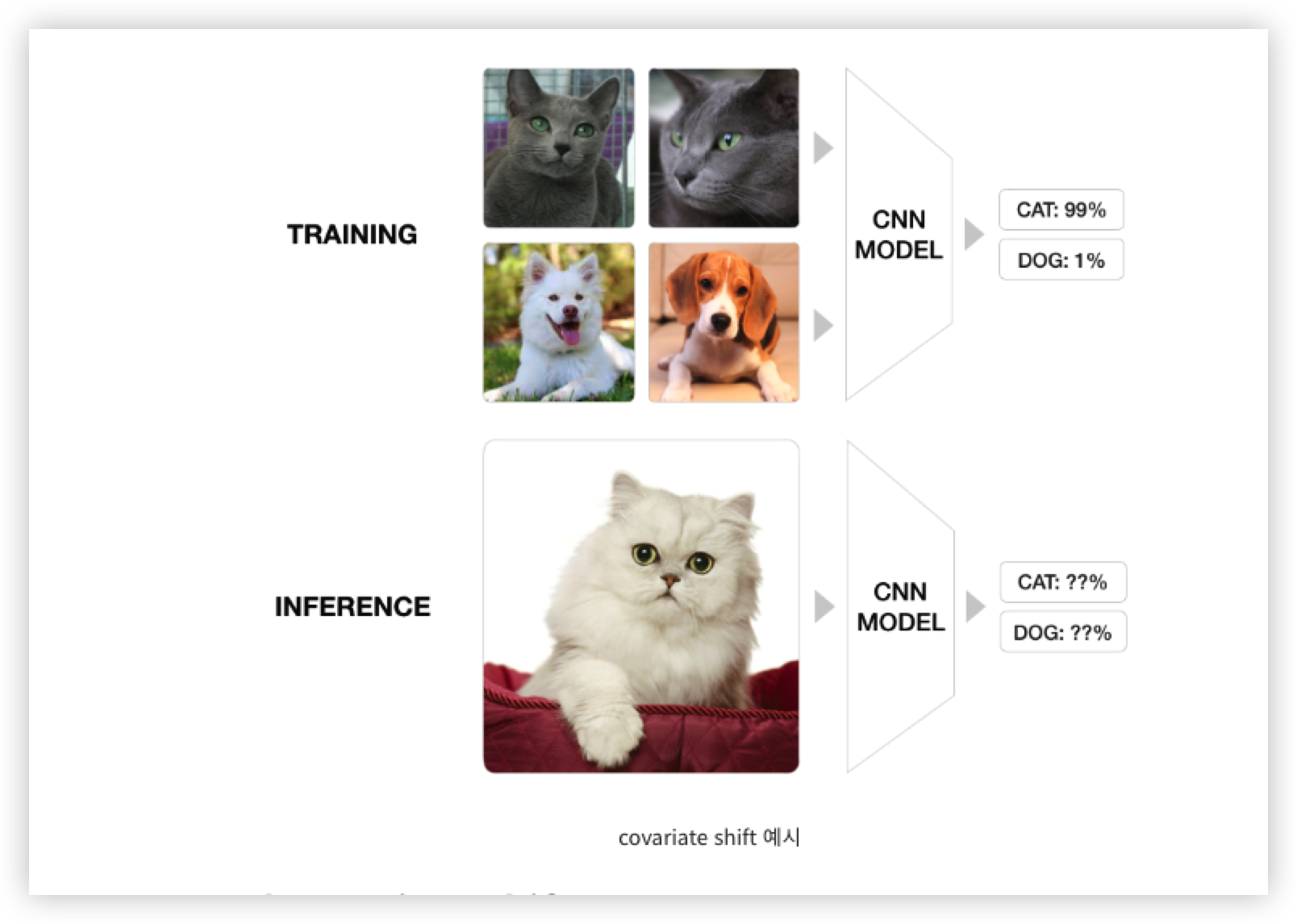
예를 들어 고양이와 강아지를 분류하는 모델을 학습시킬 때, 학습 데이터로 고양이 이미지를 '러시안 블루'종만 사용하고 테스트 데이터로 '페르시안' 종의 고양이를 분류하려고 한다면 학습 데이터의 분포와 테스트 데이터의 분포가 다르기 때문에 학습시킨 모델의 성능은 떨어질 것이며,
이처럼 학습 데이터와 테스트 데이터의 분포가 다른 것을 covariate shift 라 부른다.
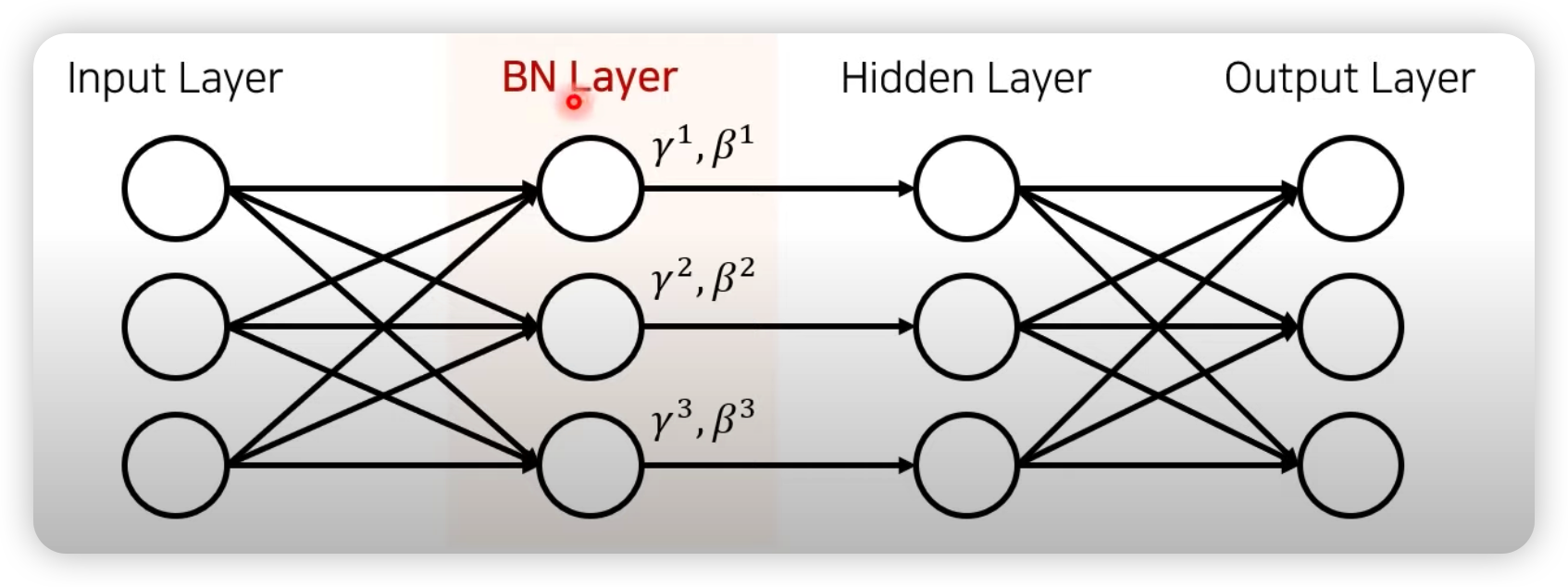
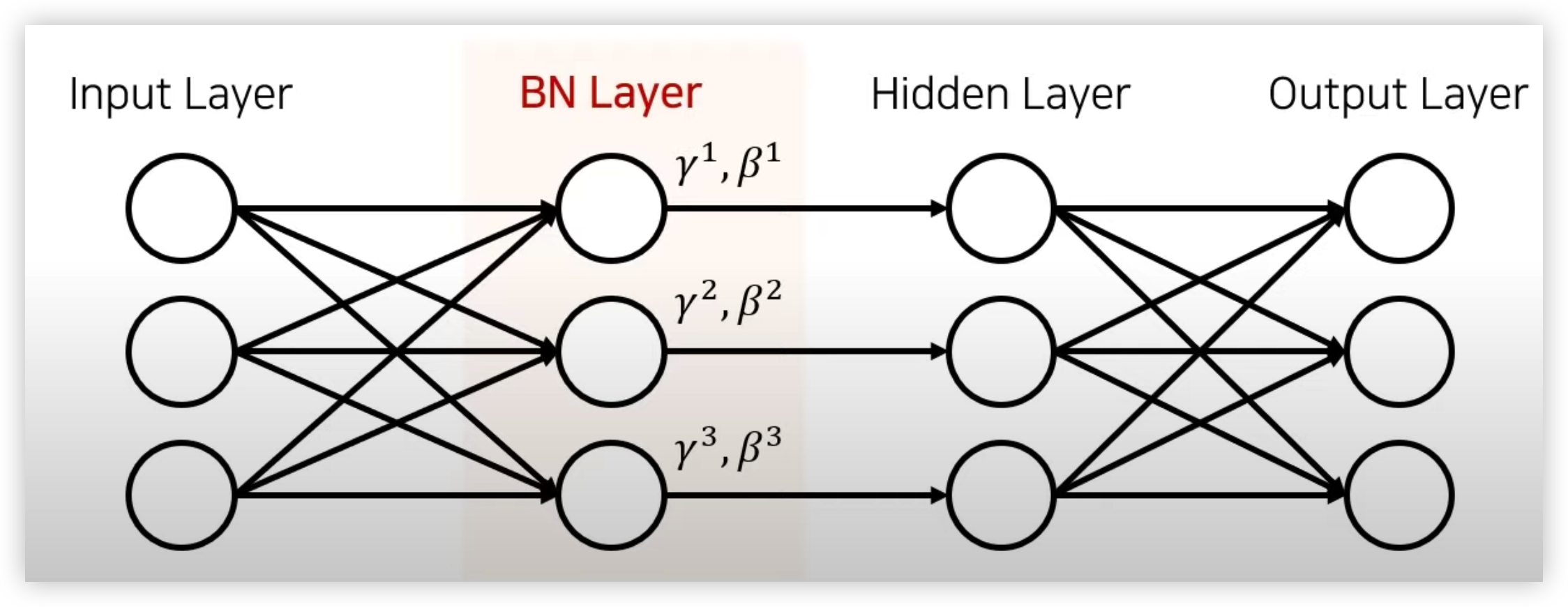
Internal Convariance Shift (ICS)
위에서 언급한 Covariate Shift(공변량 변화)가 뉴럴 네트워크 내부에서 일어나는 현상을 Internal Convaiate Shift 라고 한다.
즉 매 스탭마다 hidden layer 에 입력으로 들어오는 데이터의 분포가 달라지는 것을 의미하며 Internal Convariate Shift 는 Layer 가 깊을수록 심화될 수 있다.
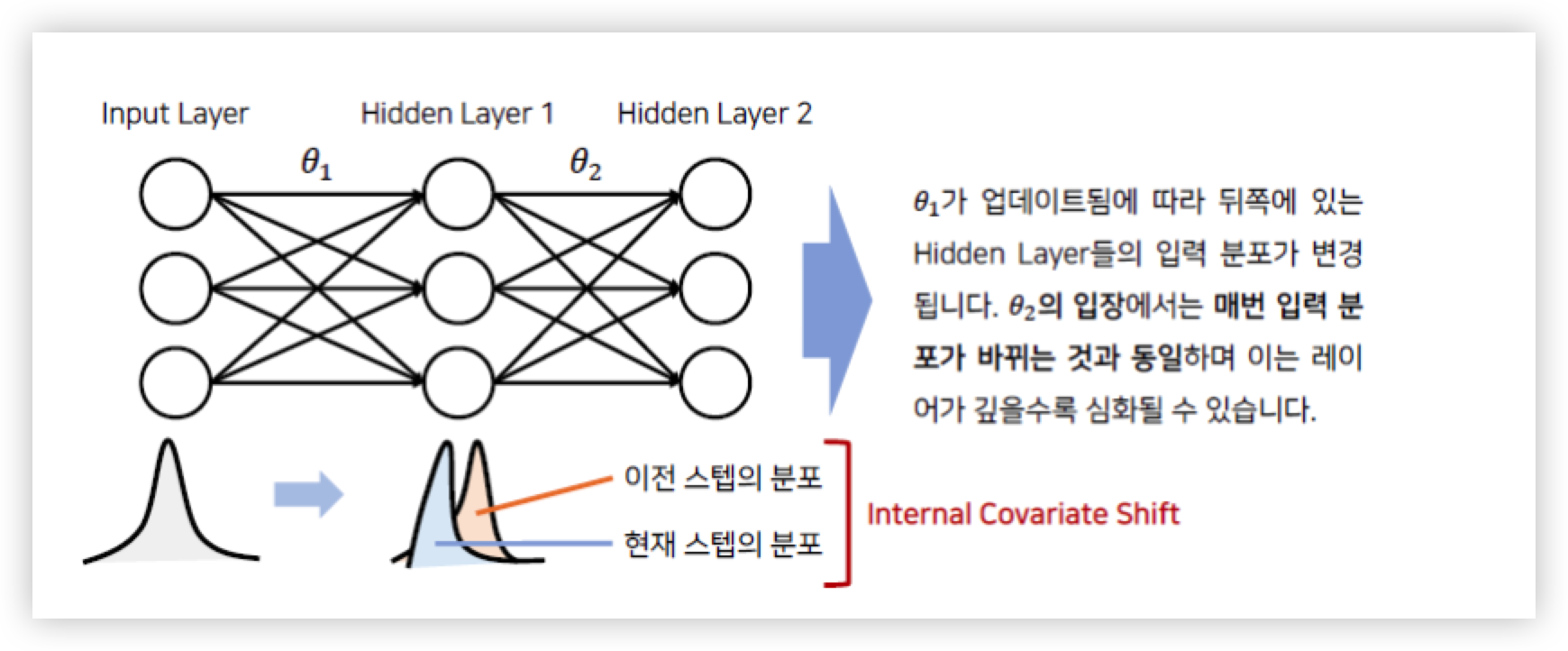
그림에서 살펴보듯이 Input Layer 에서 들어오는 Input 값은 표준화가 되서 들어오기 때문에 분포가 일정하지만, Hidden Layer 에 들어오는 입력값들은 서로 다른 Weight 값이 곱해져서 들어오기 때문에 입력 분포가 일정하지 않고 매 스텝마다 다를 수 있다.
그리고 레이어가 깊어지면 깊어질 수록 입력 분포가 더 심하게 바뀌어진다.
이러한 문제는 앞서 데이터 스케일링 챕터에서 말했듯이 데이터 분포가 다르면 학습이 잘 되지 않을 수 있는 리스크가 있다.
이러한 문제를 해결하고자 BN 저자는 Batch Normalization 도입한다면 Hidden Layer 에서도 정규화를 수행 해 각 레이어마다 모두 입력 분포를 일정하게 만들어줘서 ICS 문제를 해결한다고 주장했다.
이러한 ICS를 해결하기 위한 방법으로 Whitening 을 생각해볼 수 있다.
화이트닝(Whitening)은 데이터의 평균을 0, 그리고 공분산을 단위행렬로 갖는 정규분포 형태로 변환하는 기법으로 Decorrelation + Standardization으로 볼 수 있다.
하지만 이는 ICS 를 극복할 수 없다.
Whitening 기법이 Hidden Layer 를 정규화 할 수 없는 첫번째 이유로는
입력 데이터의 분포가 치우쳐져 있다면 데이터의 특성에 맞게 표준화(Normalization)을 해주는 것은 좋은 사실이지만, 모든 데이터들이 평균 0, 표준편차 1 이 되도록 변형시켜주는 것은 데이터를 제대로 학습하지 못한다.
왜냐하면 whitening을 하게 되면 이전 레이어로부터 학습이 가능한 parameters의 영향을 무시해버리기 때문이다.
다시말해,
- 현재 Hidden Layer의 입력 데이터 X'은 이전 레이어의 입력 데이터 X로부터 학습 가능한 파라미터(weight, bias)와 계산을 통해 나온다. X' = weigth * X + bias
- 정규화 과정에서 입력 데이터 X'의 평균(E[X'])을 입력 데이터에서 빼준다. X'' = X' - E[X']
- E[X'] = weight E[X] + bias 이므로 식을 정리하면 X'' = X' - E[X'] = weight (X - E[X])
- 이 과정에서 bias가 없어지므로 학습 가능한 파라미터의 영향이 사라져 제대로 학습이 불가능해진다.
두번째 이유로는
활성화 함수로 Sigmoid를 사용하게 되었을 때 비성형성(Non-linearity)의 특징을 잃어버리게 되는 문제가 생긴다.
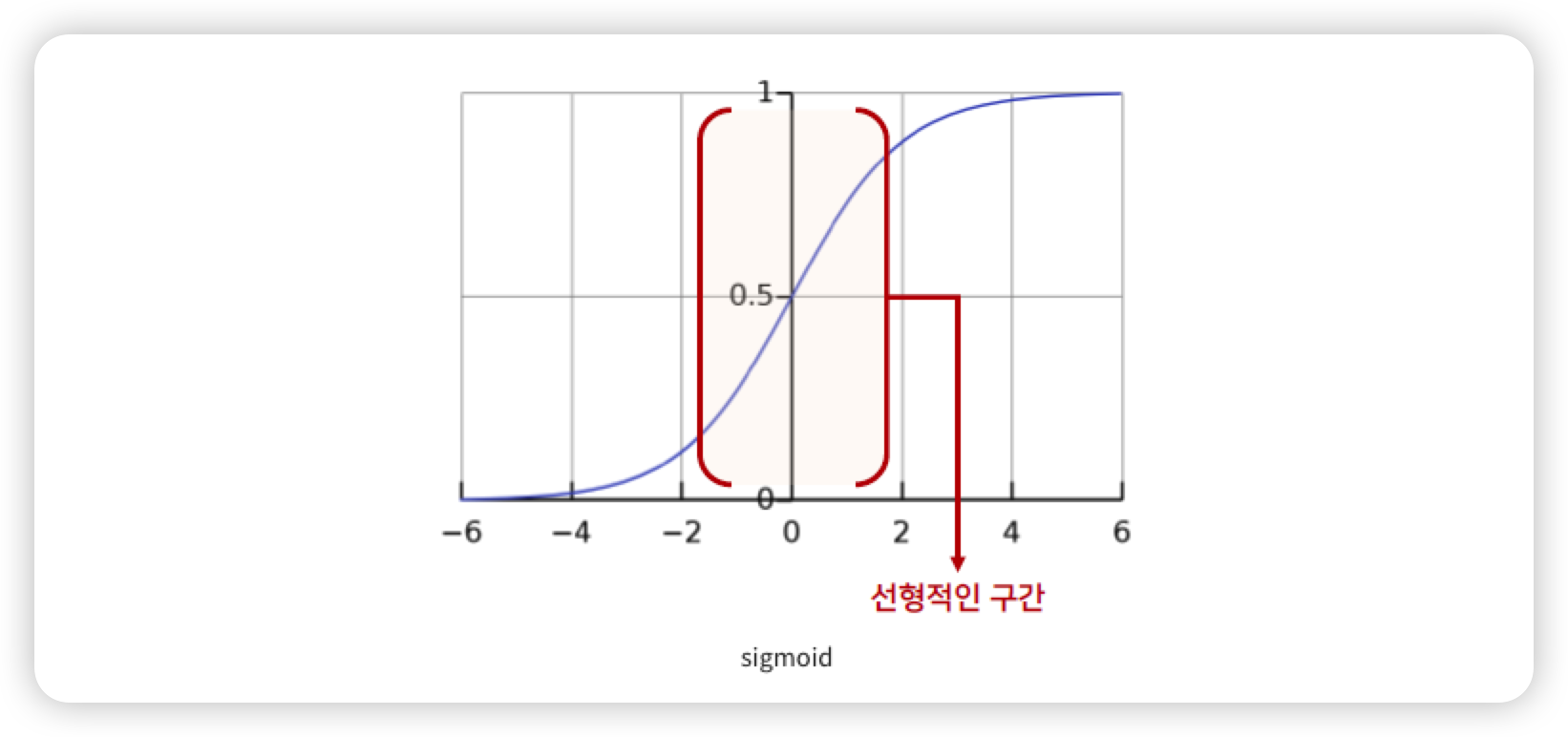
따라서 단순히 평균을 0으로 만들고 표준편차가 1이 되도록 정규화를 하는 것이 아닌, 감마(Scale), 베타(Shift) 를 통한 변환을 통해 비선형 성질을 유지 하면서 학습 될 수 있게 해주는 Batch Normalization 이 등장했다.
Batch Normalization 의 자세한 설명
Normalization 과 Standardization 은 Input Layer 에서의 입력값에 대한 데이터 스케일링이였다면, Batch Normalization 은 Hidden Layer 에 입력 값에 대한 Scaling 이다.
Batch Normalization 수식 및 방법

-
batch 안에서 평균과 분산을 계산.
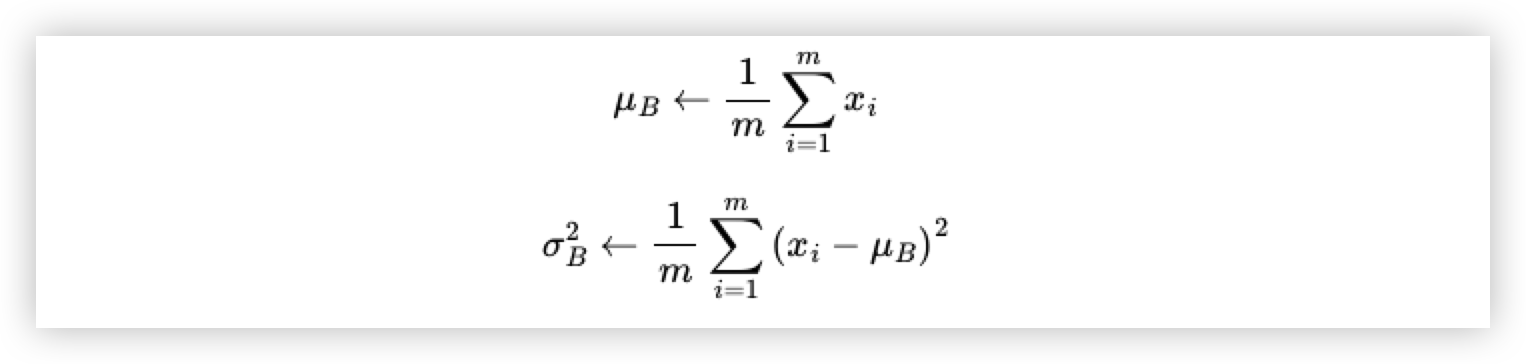
-
입력 데이터에 대한 각 차원(feature)별로 normalization을 수행. 즉 BN Layer의 각 입력 벡터마다 normalization을 수행해준다. (입실론을 추가적으로 더해주는 이유는 0으로 나누어 지는 것을 막기 위해 아주 작은 값을 더해준다.)
-
Normalization 된 값들에 대해 감마(Scale)와 베타(Shift)를 더하여 학습이 가능한 파라미터를 추가한다.
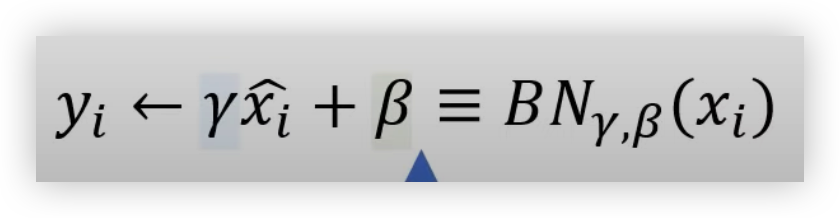

이렇게 Scale 과 Shift 파라미터를 추가해 위에서 언급했던 문제중에 하나인 Sigmoid 와 같은 활성화 함수에서 비선형성을 잃어버리는 것을 방지한다.
(sigmoid 의 선형적인 구간에서 Scale 과 Shift 파라미터를 더해줘서 비선형적인 구간에도 위치할 수 있게 하였다.)
배치 정규화의 Backpropagation 식

추론(Inference) 시의 Batch Normalization
학습 시에는 Mini Batch 의 평균과 분산을 이용할 수 있지만, 추론(Inference) 및 Test 시에는 이를 이용할 수 없다.
이러한 문제를 해결하기 위해 미리 저장해둔 Mini Batch 의 이동 평균(Moving Average)을 사용해 해결한다.
즉 Inference 전에 학습 시에 미리 Mini Batch 를 뽑을 때 Smaple Mean (샘플 평균) 및 Smaple Variance(샘플 분산)을 이용하여 각각의 이동평균을 구해놔야 한다.
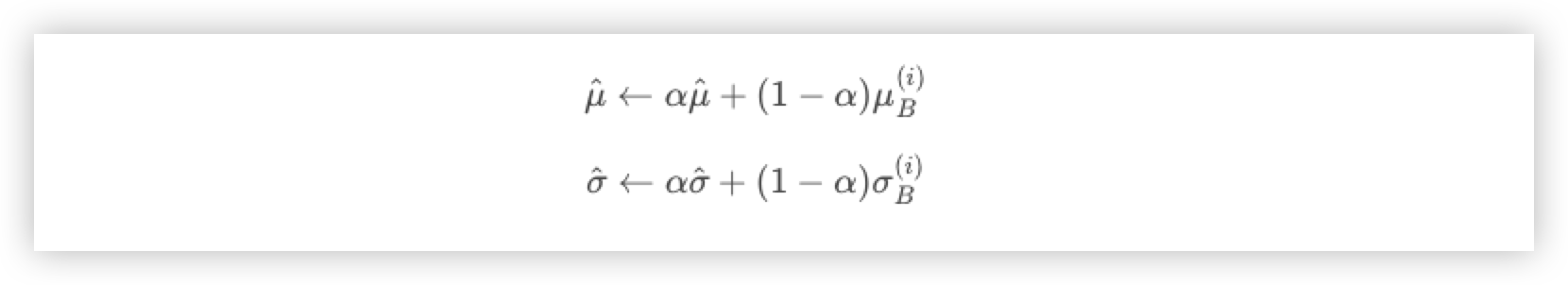
참고 Reference